Восстановите одну ветвь от 1D коэффициентов вейвлета
X = wrcoef('type',C,L,wname,N)
X = wrcoef('type',C,L,Lo_R,Hi_R,N)
X = wrcoef('type',C,L,wname)
X
= wrcoef('type',C,L,Lo_R,Hi_R)
wrcoef восстанавливает коэффициенты одномерного сигнала, учитывая структуру разложения вейвлета (C и L) и любой заданный вейвлет (wname, смотрите wfilters для получения дополнительной информации) или заданные фильтры реконструкции (Lo_R и Hi_R).
X = wrcoef( вычисляет вектор восстановленных коэффициентов, на основе структуры разложения вейвлета 'type',C,L,wname,N)[C,L] (см. wavedec для получения дополнительной информации), на уровне N. wname вектор символов или скаляр строки, содержащий имя вейвлета.
Аргумент 'type' определяет ли приближение ('type' = 'a') или деталь ('type' = 'd') коэффициенты восстановлены. Когда 'type' = 'a'N позволен быть 0; в противном случае, строго положительное число N требуется. Уровень N должно быть целое число, таким образом что N ≤ length(L)-2.
X = wrcoef( вычисляет коэффициенты как выше, учитывая фильтры реконструкции, которые вы задаете. 'type',C,L,Lo_R,Hi_R,N)
X = wrcoef( и 'type',C,L,wname)X
= wrcoef( восстановите коэффициенты максимального уровня 'type',C,L,Lo_R,Hi_R)N = length(L)-2.
% The current extension mode is zero-padding (see dwtmode).
% Load a one-dimensional signal.
load sumsin; s = sumsin;
% Perform decomposition at level 5 of s using sym4.
[c,l] = wavedec(s,5,'sym4');
% Reconstruct approximation at level 5,
% from the wavelet decomposition structure [c,l].
a5 = wrcoef('a',c,l,'sym4',5);
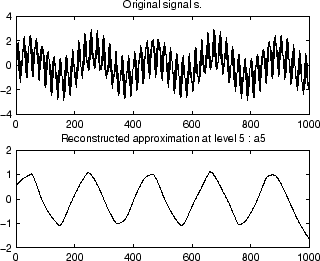
% Using some plotting commands,
% the following figure is generated.