В этом примере показано, как создать систему управления MIMO с помощью connect соединять модели Numeric LTI и настраиваемые Блоки Системы управления.
Рассмотрите следующий 2D вход, систему 2D элемента управления выводом.
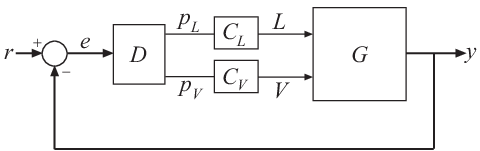
Объект G является столбцом дистилляции с двумя входными параметрами и двумя выходными параметрами. Два входных параметров являются отливом L и нагрузка кипятильника по пару V. Эти два выходных параметров являются концентрациями двух химикатов, представленных векторным y сигнала = [y 1, y 2]. Можно представлять эту модель объекта управления как:
Векторное заданное значение сигнализирует о r = [r 1, r 2] задает желаемые концентрации этих двух химикатов. Векторный сигнал ошибки e представляет вход D, статической матрице разъединения 2 на 2. CL и CV представляют независимые ПИ-контроллеры, которые управляют двумя входными параметрами G.
Создать 2D вход, 2D выходная модель, представляющая эту систему управления с обратной связью:
Создайте модель Numeric LTI, представляющую объект 2 на 2 G.
s = tf('s','TimeUnit','minutes');
G = [87.8 -86.4 ; 108.2 -109.6]/(75*s+1);
G.InputName = {'L','V'};
G.OutputName = 'y';
Когда вы создаете модель с обратной связью, connect использует имена ввода и вывода, чтобы сформировать связи между компонентами блок-схемы. Поэтому необходимо присвоить имена к вводам и выводам передаточной функции G любым из следующих способов:.
Можно присвоить имена ввода и вывода к отдельным сигналам путем определения имен сигнала в массиве ячеек, как в G.InputName = {'L','V'}
В качестве альтернативы можно использовать векторное именование сигнала, которое автоматически расширяет программное обеспечение. Например, команда G.OutputName = 'y' присваивает имена 'y(1)' и 'y(2)' к выходным параметрам G.
Создайте настраиваемые Блоки Системы управления, представляющие разъединяющийся матричный D и ПИ-контроллеры CL и CV.
D = tunableGain('Decoupler',eye(2));
D.u = 'e';
D.y = {'pL','pV'};
C_L = tunablePID('C_L','pi'); C_L.TimeUnit = 'minutes';
C_L.u = 'pL'; C_L.y = 'L';
C_V = tunablePID('C_V','pi'); C_V.TimeUnit = 'minutes';
C_V.u = 'pV'; C_V.y = 'V';u и y краткие обозначения для InputName и OutputName свойства, соответственно. Таким образом, например, ввод:
D.u = 'e';
D.y = {'pL','pV'};эквивалентно вводу:
D.InputName = 'e';
D.OutputName = {'pL','pV'};Создайте соединение подведения итогов.
Соединение подведения итогов производит сигналы ошибки e путем взятия различия между r и y.
Sum = sumblk('e = r - y',2);Sum представляет передаточную функцию для соединения подведения итогов, описанного формулой 'e = r - y'. Второй аргумент к sumblk указывает что вводы и выводы Sum каждый векторные сигналы длины 2. Программное обеспечение поэтому автоматически присваивает имена сигнала {'r(1)','r(2)','y(1)','y(2)'} к Sum.InputName и {'e(1)','e(2)'} к Sum.OutputName.
Соедините все компоненты, чтобы создать систему с обратной связью от r до y.
CLry = connect(G,D,C_L,C_V,Sum,'r','y');
Аргументы к connect функция включает все компоненты системы с обратной связью в любом порядке. connect автоматически комбинирует компоненты с помощью имен ввода и вывода, чтобы соединить сигналы.
Последние два аргумента к connect задайте выход и входные сигналы модели с обратной связью, соответственно. Получившийся genss модель CLry имеет 2D входные параметры и два выходных параметров.