System identification является методологией для того, чтобы создать математические модели динамических систем с помощью измерений сигналов ввода и вывода системы.
Процесс системы идентификации требует что вы:
Измерьте сигналы ввода и вывода от своей системы вовремя или частотного диапазона.
Выберите структуру модели.
Примените метод оценки оценить значение для корректируемых параметров в структуре модели кандидата.
Оцените предполагаемую модель, чтобы видеть, достаточна ли модель для ваших потребностей приложения.
В динамической системе значения выходных сигналов зависят и от мгновенных значений ее входных сигналов и от также на прошлом поведении системы. Например, автокресло является динамической системой — форма места (улаживающий положение) зависит и от текущего веса пассажира (мгновенное значение) и от сколько времени этот пассажир ехал в автомобиле (прошлое поведение).
model является математическим отношением между переменными ввода и вывода системы. Модели динамических систем обычно описываются дифференциальными или разностными уравнениями, передаточными функциями, уравнениями пространства состояний и моделями нулевого усиления полюса.
Можно представлять динамические модели и в форме непрерывного времени и дискретного времени.
Часто используемым примером динамической модели является уравнение движения системы пружинного массового демпфера. Как показано в следующей фигуре, масса перемещает в ответ на силу F (t), примененный на основу, к которой присоединяется масса. Ввод и вывод этой системы является силой F (t) и смещение y (t) соответственно.
Система массового демпфера Spring, взволнованная силой F (t)
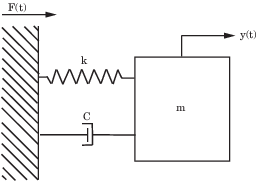
Можно представлять ту же физическую систему как несколько эквивалентных моделей. Например, можно представлять систему массового пружинного демпфера в непрерывное время как дифференциальное уравнение второго порядка:
где m является массой, k постоянная жесткость пружины, и c коэффициент демпфирования. Решение этого дифференциального уравнения позволяет вам определить смещение массы, y (t), как функция внешней силы F (t) в любое время t для известных значений постоянного m, c и k.
Рассмотрите смещение, y (t) и скорость, , как переменные состояния:
Можно выразить предыдущее уравнение движения как модель в пространстве состояний системы:
Матрицы A, B и C связаны с константами m, c и k можно следующим образом:
Можно также получить transfer function model системы пружинного массового демпфера путем взятия Преобразования Лапласа дифференциального уравнения:
где s является переменной Лапласа.
Предположим, что можно только наблюдать переменные F ввода и вывода (t) и y (t) системы массового пружинного демпфера в моменты дискретного времени t = n Ts, где Ts является фиксированным временным интервалом и n = 0, 1, 2.... Переменные, как говорят, производятся с шагом расчета Ts. Затем можно представлять отношение между произведенными переменными ввода - вывода как разностное уравнение второго порядка, такими как:
Часто, для простоты, Ts взят в качестве одной единицы измерения времени, и уравнение может быть записано как:
где a1 и a2 являются параметрами модели. Параметры модели связаны с системными константами m, c, и k и шаг расчета Ts.
Это разностное уравнение показывает динамический характер модели. Значение смещения в то время мгновенный t зависит не только от значения силы F в предыдущий раз момент, но также и на значениях смещения в предыдущие два раза моменты y (t –1) и y (t –2).
Можно использовать это уравнение, чтобы вычислить смещение в определенное время. Смещение представлено как взвешенная сумма прошлых значений ввода и вывода:
Это уравнение показывает итеративный способ генерация значения выхода y (t), начинающий с начальных условий (y (0) и y (1)) и измерения входа F (t). Этот расчет называется simulation.
В качестве альтернативы выходное значение в установленный срок t может быть вычислено с помощью измеренных значений выхода в предыдущие два раза моменты и входное значение в предыдущий раз момент. Этот расчет называется prediction. Для получения дополнительной информации о симуляции и предсказании с помощью модели, смотрите темы на странице Simulation и Prediction.
Можно также представлять уравнение дискретного времени движения в пространстве состояний и формах передаточной функции путем выполнения преобразований, похожих на описанных в Примере Динамической модели Непрерывного времени.
Система идентификации использует сигналы ввода и вывода, которые вы измеряете от системы, чтобы оценить значения корректируемых параметров в данной структуре модели.
Получение хорошей модели вашей системы зависит от того, как хорошо ваши результаты измерений отражают поведение системы. Смотрите Требования Качества данных.
Используя этот тулбокс, вы создаете модели с помощью сигналов ввода - вывода временного интервала, данных о частотной характеристике, сигналов временных рядов и спектров timeseries.
Данные временного интервала состоят из переменных ввода и вывода системы, которую вы записываете в универсальном интервале выборки в течение времени.
Например, если вы измеряете входную силу, F (t) и массовое смещение, y (t), системы пружинного массового демпфера в универсальной частоте дискретизации 10 Гц, вы получаете следующие векторы измеренных значений:
где Ts = 0,1 секунды и N Ts время последнего измерения.
Если вы хотите создать модель дискретного времени из этих данных, векторы данных umeas и ymeas и шаг расчета, Ts предоставляет достаточную информацию для создания такой модели.
Если вы хотите создать модель непрерывного времени, необходимо также знать междемонстрационное поведение входных сигналов во время эксперимента. Например, вход может быть кусочной константой (нулевой порядок содержат), или кусочный линейный (хранение первого порядка) между выборками.
Данные о частотном диапазоне представляют измерения системных переменных ввода и вывода, которые вы записываете или храните в частотном диапазоне. Сигналы частотного диапазона являются преобразованиями Фурье соответствующих сигналов области времени.
Данные о частотном диапазоне могут также представлять частотную характеристику системы, представленной набором комплексных значений ответа по данному частотному диапазону. frequency response описывает выходные параметры к синусоидальным входным параметрам. Если вход является синусоидой с частотой ω, то выход является также синусоидой той же частоты, амплитудой которой является A (ω) времена амплитуда входного сигнала и сдвиг фазы Φ (ω) относительно входного сигнала. Частотной характеристикой является A (ω) e (iΦ(ω)).
В случае системы массового пружинного демпфера можно получить данные о частотной характеристике при помощи синусоидальной входной силы и измерения соответствующего амплитудного усиления и сдвига фазы ответа в области значений входных частот.
Можно использовать данные частотного диапазона, чтобы создать и дискретное время и модели непрерывного времени системы.
Система идентификации требует что ваш сбор данных важная динамика вашей системы. Хороший экспериментальный план гарантирует, что вы измеряете правильные переменные с достаточной точностью и длительностью, чтобы получить динамику, которую вы хотите смоделировать. В общем случае ваш эксперимент должен:
Используйте входные параметры, которые волнуют системную динамику соответственно. Например, один шаг является достаточно редко возбуждением.
Измерьте данные достаточно долго, чтобы получить важные постоянные времени.
Настройте систему сбора данных, чтобы иметь хорошее отношение сигнал-шум.
Измерьте данные в соответствующих интервалах выборки или разрешении частоты.
Можно анализировать качество данных прежде, чем создать модель с помощью методов, доступных в программном обеспечении Signal Processing Toolbox. Например, анализируйте входные спектры, чтобы определить, имеют ли входные сигналы достаточную силу по пропускной способности системы.
Можно также анализировать данные, чтобы определить пиковые частоты, ввести задержки, важные постоянные времени и индикацию относительно нелинейности с помощью непараметрических аналитических инструментов в этом тулбоксе. Можно использовать эту информацию в конфигурировании структур модели для того, чтобы создать модели из данных. Для получения дополнительной информации см.:
model structure является математическим отношением между переменными ввода и вывода, которое содержит неизвестные параметры. Примерами структур модели являются передаточные функции с корректируемыми полюсами и нулями, уравнениями пространства состояний с неизвестными системными матрицами и нелинейными параметрированными функциями.
Следующее разностное уравнение представляет простую структуру модели:
где a и b являются корректируемыми параметрами.
Процесс системы идентификации требует, чтобы вы выбрали структуру модели и применили методы оценки определить численные значения параметров модели.
Можно использовать один из следующих подходов, чтобы выбрать структуру модели:
Вы хотите модель, которая может воспроизвести ваши результаты измерений и максимально проста. Можно попробовать различные математические структуры, доступные в тулбоксе. Этот подход моделирования называется моделированием черного ящика.
Вы хотите определенную структуру для своей модели, которую вы, возможно, вывели из первых принципов, но не знаете численные значения ее параметров. Можно затем представлять структуру модели как набор уравнений или системы в пространстве состояний в MATLAB® и оценить значения его параметров из данных. Этот подход известен как моделирование серого ящика.
Программное обеспечение System Identification Toolbox™ оценивает параметры модели путем минимизации ошибки между выходом модели и измеренным ответом. Выходом ymodel линейной модели дают:
Модель y (t) = G u (t)
где G является передаточной функцией.
Чтобы определить G, тулбокс минимизирует различие между моделью выхода y модели (t) и измеренным выходом y meas (t). minimization criterion является взвешенной нормой ошибки, v (t), где:
v (t) = ymeas (t) – ymodel (t).
ymodel (t) является одним из следующего:
Симулированный ответ (G u (t) модели для данного входа u (t)
Предсказанный ответ модели для данного входа u (t) и прошлые измерения выхода (ymeas (t-1), ymeas (t-2)...)
Соответственно, ошибка v (t) называется simulation error или prediction error. Алгоритмы оценки настраивают параметры в структуре модели G, таким образом, что норма этой ошибки как можно меньше.
Можно сконфигурировать алгоритм оценки:
Конфигурируя критерий минимизации, чтобы фокусировать оценку желаемый частотный диапазон, такой, как поставили больше акцента на более низких частотах и преуменьшить роль более высоких вкладов шума частоты. Можно также сконфигурировать критерий, чтобы предназначаться для потребностей применения по назначению в модели, таких как симуляция или предсказание.
Определение опций оптимизации для итеративных алгоритмов оценки.
Большинство алгоритмов оценки в этом тулбоксе является итеративным. Можно сконфигурировать итеративный алгоритм оценки путем определения опций, таких как метод оптимизации и максимальное количество итераций.
Для получения дополнительной информации о конфигурировании алгоритма оценки, см. Опции, чтобы Сконфигурировать Функцию потерь и темы для оценки определенных структур модели.
Моделирование черного ящика полезно, когда ваш главный интерес находится в подгонке данных независимо от конкретной математической структуры модели. Тулбокс обеспечивает несколько линейных и нелинейных структур модели черного ящика, которые традиционно были полезны для представления динамических систем. Эти структуры модели варьируются по сложности в зависимости от гибкости, необходимо объяснить динамику и шум в системе. Можно выбрать одну из этих структур и вычислить его параметры, чтобы соответствовать измеренным данным об ответе.
Моделирование черного ящика обычно является эмпирическим процессом, где вы оцениваете параметры различных структур и сравниваете результаты. Как правило, вы начинаете с простой линейной структуры модели и продвижения к более комплексным структурам. Вы можете также выбрать структуру модели, потому что вы более знакомы с этой структурой или потому что у вас есть определенные потребности приложения.
Самые простые линейные структуры черного ящика требуют, чтобы наименьшее количество опций сконфигурировало:
Передаточная функция, с данным количеством полюсов и нулей.
Линейная модель ARX, которая является самой простой моделью полинома ввода - вывода.
Модель в пространстве состояний, которую можно оценить путем определения количества состояний модели
Оценка некоторых из этих структур также использует неитеративные алгоритмы оценки, который далее уменьшает сложность.
Можно сконфигурировать структуру модели с помощью model order. Определение порядка модели варьируется в зависимости от типа модели, которую вы выбираете. Например, если вы выбираете представление передаточной функции, порядок модели связан с количеством полюсов и нулей. Для представления пространства состояний порядок модели соответствует количеству состояний. В некоторых случаях, такой что касается линейного ARX и структур модели в пространстве состояний, можно оценить порядок модели от данных.
Если простые структуры модели не производят хорошие модели, можно выбрать структуры более сложной модели:
Определение более высокого порядка модели для той же линейной структуры модели. Более высокий порядок модели увеличивает гибкость модели для получения комплексных явлений. Однако излишне старшие разряды могут сделать модель менее надежной.
Явным образом моделирование шума:
y (t) =Gu (t) +He (t)
где модели H аддитивное воздействие путем обработки воздействия как выхода линейной системы, управляемой белым источником шума e (t).
Используя структуру модели, которая явным образом моделирует аддитивное воздействие, может помочь улучшить точность измеренного G компонента. Кроме того, такая структура модели полезна, когда ваш главный интерес использует модель в предсказании будущих значений ответа.
Используя различную линейную структуру модели.
Смотрите линейные структуры модели.
Используя нелинейную структуру модели.
Нелинейные модели имеют больше гибкости в получении комплексных явлений, чем линейные модели подобных порядков. Смотрите Нелинейные Структуры модели.
В конечном счете вы выбираете самую простую структуру модели, которая обеспечивает лучшую подгонку к вашим результатам измерений. Для получения дополнительной информации смотрите Оценку Линейных Моделей Используя Быстрый запуск.
Независимо от структуры вы выбираете для оценки, можно упростить модель для потребностей приложения. Например, можно выделить измеренную динамику (G) от шумовой динамики (H), чтобы получить более простую модель, которая представляет только отношение между y и u. Можно также линеаризовать нелинейную модель о рабочей точке.
Линейная модель часто достаточна, чтобы точно описать системную динамику и, в большинстве случаев, необходимо сначала попытаться подбирать линейные модели. Если линейный выход модели не соответственно воспроизводит измеренный выход, вы можете должны быть использовать нелинейную модель.
Можно оценить потребность использовать нелинейную структуру модели путем графического вывода ответа системы к входу. Если вы замечаете, что ответы отличаются в зависимости от уровня на входе или вводят знак, попытайтесь использовать нелинейную модель. Например, если выходной ответ на вход подходит, быстрее, чем ответ на шаг вниз, вам может быть нужна нелинейная модель.
Прежде, чем создать нелинейную модель системы, которую вы знаете, нелинейно, попытайтесь преобразовать переменные ввода и вывода, таким образом, что отношение между преобразованными переменными линейно. Например, рассмотрите систему, которая имеет текущий и напряжение как входные параметры к спирали для нагрева воды и температура горячей жидкости как выход. Выход зависит от входных параметров через степень нагревателя, который равен продукту тока и напряжения. Вместо того, чтобы создать нелинейную модель для этого 2D входа и системы с одним выходом, можно создать новую входную переменную путем взятия продукта текущих и напряжения и затем создать линейную модель, которая описывает отношение между степенью и температурой.
Если вы не можете определить переменные преобразования, которые дают к линейному соотношению между переменными ввода и вывода, можно использовать нелинейные структуры, такие как Нелинейный ARX или модели Хаммерстайна-Винера. Для списка поддерживаемых нелинейных структур модели и когда использовать их, смотрите Нелинейные Структуры модели.
Можно использовать приложение System Identification или команды, чтобы оценить линейные и нелинейные модели различных структур. В большинстве случаев вы выбираете структуру модели и оцениваете параметры модели с помощью одной команды.
Рассмотрите систему массового пружинного демпфера, описанную приблизительно в Динамических системах и Моделях. Если вы не знаете уравнение движения этой системы, можно использовать подход моделирования черного ящика, чтобы создать модель. Например, можно оценить передаточные функции или модели в пространстве состояний путем определения порядков этих структур модели.
Передаточная функция является отношением полиномов:
Для массово-пружинной системы демпфера эта передаточная функция:
который является системой без нулей и 2 полюсов.
В дискретное время передаточная функция системы массового пружинного демпфера может быть:
где порядки модели соответствуют количеству коэффициентов числителя и знаменателя (nb = 1 и nf = 2) и задержка ввода - вывода равняется экспоненте самой низкоуровневой z –1 в числителе (nk = 1).
В непрерывное время можно создать линейную модель передаточной функции использование tfest команда:
m = tfest(data,2,0)
где data ваши измеренные данные ввода - вывода, представленные как iddata возразите и порядок модели является набором количества полюсов (2) и количества нулей (0).
Точно так же можно создать структуру модели Output Error дискретного времени с помощью следующей команды:
m = oe(data,[1 2 1])
Порядком модели является [nb nf nk] = [1 2 1]. Обычно, вы не знаете порядков модели заранее. Необходимо попробовать несколько стоимостей заказов модели, пока вы не находите порядки, которые производят приемлемую модель.
В качестве альтернативы можно выбрать структуру пространства состояний, чтобы представлять систему массового пружинного демпфера и оценить параметры модели с помощью ssest или n4sid команда:
m = ssest(data,2)
где order= 2 представляет количество состояний в модели.
В моделировании черного ящика вам не нужно уравнение системы движения — только предположение порядков модели.
Для получения дополнительной информации о создавании моделей, смотрите Шаги для Использования Приложения System Identification и Команд Оценки Модели.
В некоторых ситуациях можно вывести структуру модели из физических принципов. Например, математическое отношение между входной силой и получившимся массовым смещением в системе массового пружинного демпфера известно. В форме пространства состояний моделью дают:
где xT) = [yTVT)] вектор состояния. Коэффициенты A, B и C являются функциями параметров модели:
A = [0 1; –k/m –c/m]
B = [0; 1/m]
C = [1 0]
Здесь, вы полностью знаете структуру модели, но не знаете значений ее параметров — m, c и k.
В подходе серого ящика вы используете данные, чтобы оценить значения неизвестных параметров вашей структуры модели. Вы задаете структуру модели набором дифференциальных или разностных уравнений в MATLAB и обеспечиваете некоторое исходное предположение для неизвестных заданных параметров.
В общем случае вы создаете модели серого ящика:
Создание структуры модели шаблона.
Конфигурирование параметров модели с начальными значениями и ограничениями (если таковые имеются).
Применение метода оценки для структуры модели и вычисление значений параметра модели.
Следующая таблица обобщает способы, которыми можно задать структуру модели серого ящика.
| Представление структуры серого ящика | Узнать больше |
|---|---|
|
Представляйте структуру модели в пространстве состояний как структурированный Можно вычислить значения параметров, такие как m, c и k, из матриц пространства состояний A и B. Например, m = 1/B (2) и k = –A (2,1) m. | |
Представляйте структуру модели в пространстве состояний как idgrey объект модели. Можно непосредственно оценить значения параметров mC и k. | Оценка Модели Серого Ящика |
После того, как вы оцените модель, можно оценить качество модели:
В конечном счете необходимо оценить качество основанного на модели на том, обращается ли модель соответственно к потребностям приложения. Для получения информации о других доступных методах анализа модели смотрите Анализ модели.
Если вы не получаете удовлетворительную модель, можно итеративно улучшить результаты путем попытки различной структуры модели, изменения настроек алгоритма оценки или выполнения дополнительной обработки данных. Если эти изменения не улучшают ваши результаты, вы можете должны быть пересмотреть свой экспериментальный план и процедуры сбора данных.
Как правило, вы оцениваете качество модели путем сравнения ответа модели на измеренный выход для того же входного сигнала.
Предположим, что вы используете подход моделирования черного ящика, чтобы создать динамические модели пружинно-массовой системы демпфера. Вы пробуете различные структуры модели и порядки, такие как:
model1 = arx(data, [2 1 1]); model2 = n4sid(data, 3)
Можно симулировать эти модели с конкретным входом и выдержать сравнение, их ответы против измеренных значений смещения для того же входа применились к действительной системе. Следующая фигура сравнивает симулированные и измеренные ответы для входа шага.
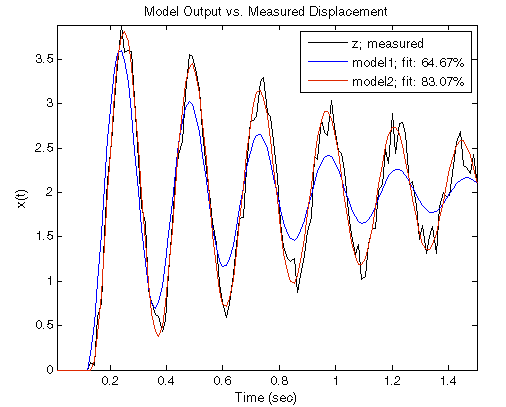
Предыдущая фигура указывает на тот model2 лучше, чем model1 потому что model2 лучшие подгонки данные (65% по сравнению с 83%).
Подгонка % указывает на соглашение между ответом модели и измеренным выходом: 100 средних значений совершенная подгонка, и 0 указывает на плохую подгонку (то есть, выход модели имеет ту же подгонку к измеренному выходу как среднее значение измеренного выхода).
Для получения дополнительной информации смотрите темы на странице Compare Output with Measured Data.
Программное обеспечение System Identification Toolbox позволяет вам выполнить остаточный анализ, чтобы оценить качество модели. Остаточные значения представляют фрагмент выходных данных, не объясненных предполагаемой моделью. Хорошая модель имеет остаточные значения, некоррелированые с прошлыми входными параметрами.
Для получения дополнительной информации смотрите темы на странице Residual Analysis.
Когда вы оцениваете параметры модели из данных, вы получаете их номинальную стоимость, которая является с точностью до области доверия. Размер этой области определяется значениями неопределенности параметра, вычисленной во время оценки. Величина неопределенности обеспечивает меру надежности модели. Большая неопределенность в параметрах может следовать из излишне высоких порядков модели, несоответствующих уровней возбуждения во входных данных и плохого отношения сигнал-шум в результатах измерений.
Можно вычислить и визуализировать эффект неопределенности параметра на ответе модели вовремя и частотных диапазонах с помощью нулевых полюсом карт, Предвещать ответ и переходные процессы. Например, в следующей Диаграмме Боде предполагаемой модели, теневые области представляют неопределенность в амплитуде и фазе частотной характеристики модели, вычисленное использование неопределенности в параметрах. График показывает, что неопределенность находится низко только в частотном диапазоне на 5 - 50 рад/с, который указывает, что модель надежна только в этом частотном диапазоне.
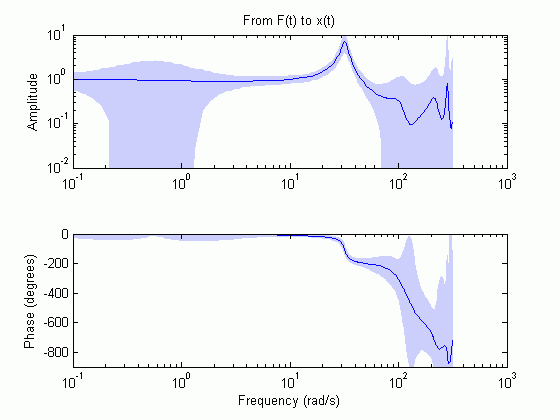
Для получения дополнительной информации смотрите, Вычисляют Неопределенность Модели.
Документация System Identification Toolbox предоставляет вам необходимую информацию, чтобы использовать этот продукт. Дополнительные ресурсы доступны, чтобы помочь вам узнать больше об определенных аспектах теории системы идентификации и приложений.
Следующая книга описывает методы для системы идентификации и физического моделирования:
| Ljung, L. и Т. Глэд. Моделирование динамических систем. PTR Prentice Hall, верхний Сэддл-Ривер, NJ, 1994. |
Эти книги предоставляют подробную информацию о теории системы идентификации и алгоритмах:
Ljung, L. System Identification: Теория для Пользователя. Второй выпуск. PTR Prentice Hall, Верхний Сэддл-Ривер, NJ, 1999.
Söderström, T. и П. Стойка. System Identification. Prentice Hall International, Лондон, 1989.
Для получения информации о работе с данными частотного диапазона см. следующую книгу:
| Pintelon, R. и Дж. Шоукенс. System Identification. Подход частотного диапазона. Вайли-ИИ-Пресс, Нью-Йорк, 2001. |
Для получения информации о нелинейной идентификации смотрите следующие ссылки:
Sjöberg, J., Ц. Чжан, Л. Лджанг, А. Бенвенист, Б. Деилон, П. Глореннек, Х. Яльмарссон и А. Юдицкий, “Нелинейное Моделирование Черного ящика в System Identification: Объединенный Обзор”. Automatica. Издание 31, Выпуск 12, 1995, стр 1691–1724.
Juditsky, A., Х. Яльмарссон, А. Бенвенист, Б. Делион, Л. Лджанг, Дж. Сйоберг и Ц. Чжан, “Нелинейные Модели Черного ящика в System Identification: Математические Основы”. Automatica. Издание 31, Выпуск 12, 1995, стр 1725–1750.
Чжан, Q. и А. Бенвенист, “Сети вейвлета”. Транзакции IEEE на Нейронных сетях. Издание 3, Выпуск 6, 1992, стр 889–898.
Чжан, Q., “Используя Сеть Вейвлета по Непараметрической Оценке”. Транзакции IEEE на Нейронных сетях. Издание 8, Выпуск 2, 1997, стр 227–236.
Для получения дополнительной информации о системах и сигналах, см. следующую книгу:
| Оппенхейм, J., и Willsky, A.S. Сигналы и системы. PTR Prentice Hall, верхний Сэддл-Ривер, NJ, 1985. |
Следующий учебник описывает числовые методы для оценки параметра с помощью минимизации критерия:
| Деннис, J.E., младший, и Р.Б. Шнабель. Численные методы для оптимизации без ограничений и нелинейных уравнений. PTR Prentice Hall, верхний Сэддл-Ривер, NJ, 1983. |