Exponenta Banner

interp2

Интерполяция для 2D данных с координатной сеткой в meshgrid формате

свернуть все на странице

Синтаксис

Vq = interp2(X,Y,V,Xq,Yq)
Vq = interp2(V,Xq,Yq)
Vq = interp2(V)
Vq = interp2(V,k)
Vq = interp2(___,method)
Vq = interp2(___,method,extrapval)

Описание

пример

Vq = interp2(X,Y,V,Xq,Yq) возвращает интерполированные значения функции двух переменных в определенных точках запроса с помощью линейной интерполяции. Результаты всегда проходят через исходную выборку функции. X и Y содержите координаты точек выборки. V содержит соответствующие значения функции в каждой точке выборки. Xq и Yq содержите координаты точек запроса.

Vq = interp2(V,Xq,Yq) принимает сетку по умолчанию точек выборки. Узлы решетки по умолчанию покрывают прямоугольную область, X=1:n и Y=1:m, где [m,n] = size(V). Используйте этот синтаксис, когда это необходимо, чтобы сохранить память, и не касаются абсолютных расстояний между точками.

Vq = interp2(V) возвращает интерполированные значения на усовершенствованной сетке, сформированной путем деления интервала между демонстрационными значениями однажды в каждой размерности.

пример

Vq = interp2(V,k) возвращает интерполированные значения на усовершенствованной сетке, сформированной путем повторного сокращения вдвое интервалов k времена в каждой размерности. Это приводит к 2^k-1 интерполированные точки между демонстрационными значениями.

пример

Vq = interp2(___,method) задает альтернативный метод интерполяции: 'linear'самый близкий, 'cubic', 'makima', или 'spline'. Методом по умолчанию является 'linear'.

пример

Vq = interp2(___,method,extrapval) также задает extrapval, скалярное значение, которое присвоено всем запросам, которые лежат вне области точек выборки.

Если вы не используете extrapval аргумент для запросов вне области точек выборки, затем на основе method аргумент interp2 возвращает одно из следующего:

  • Экстраполируемые значения для 'spline' и 'makima' методы

  • NaN значения для других методов интерполяции

Примеры

свернуть все

Скрипт Open Live Script

Грубо произведите peaks функция. 

[X,Y] = meshgrid(-3:3);
V = peaks(X,Y);

Постройте крупную выборку. 

figure
surf(X,Y,V)
title('Original Sampling');

Создайте сетку запроса с разрядкой 0,25. 

[Xq,Yq] = meshgrid(-3:0.25:3);

Интерполируйте в точках запроса. 

Vq = interp2(X,Y,V,Xq,Yq);

Постройте результат. 

figure
surf(Xq,Yq,Vq);
title('Linear Interpolation Using Finer Grid');

Скрипт Open Live Script

Грубо произведите функцию peaks. 

[X,Y] = meshgrid(-3:3);
V = peaks(7);

Постройте крупную выборку. 

figure
surf(X,Y,V)
title('Original Sampling');

Создайте сетку запроса с разрядкой 0,25. 

[Xq,Yq] = meshgrid(-3:0.25:3);

Интерполируйте в точках запроса и задайте кубичную интерполяцию. 

Vq = interp2(X,Y,V,Xq,Yq,'cubic');

Постройте результат. 

figure
surf(Xq,Yq,Vq);
title('Cubic Interpolation Over Finer Grid');

Скрипт Open Live Script

Загрузите некоторые данные изображения в рабочую область. 

load flujet.mat
colormap gray

Изолируйте небольшую область изображения и бросьте его к с одинарной точностью.

V = single(X(200:300,1:25));

Отобразите область изображений. 

imagesc(V);
axis off
title('Original Image')

Вставьте интерполированные значения путем повторного деления интервалов между точками усовершенствованной сетки пять раз в каждой размерности. 

Vq = interp2(V,5);

Отобразите результат. 

imagesc(Vq);
axis off
title('Linear Interpolation')

Скрипт Open Live Script

Грубо произведите функцию в области значений, [-2, 2] в обеих размерностях. 

[X,Y] = meshgrid(-2:0.75:2);
R = sqrt(X.^2 + Y.^2)+ eps;
V = sin(R)./(R);

Постройте крупную выборку. 

figure
surf(X,Y,V)
xlim([-4 4])
ylim([-4 4])
title('Original Sampling')

Создайте сетку запроса, которая расширяет вне области X и Y. 

[Xq,Yq] = meshgrid(-3:0.2:3);

Выполните кубичную интерполяцию в области X и Y, и присвойте все запросы, которые идут снаружи, чтобы обнулить. 

Vq = interp2(X,Y,V,Xq,Yq,'cubic',0);

Постройте результат. 

figure
surf(Xq,Yq,Vq)
title('Cubic Interpolation with Vq=0 Outside Domain of X and Y');

Входные параметры

свернуть все

Демонстрационные узлы решетки в виде действительных матриц или векторов. Демонстрационные узлы решетки должны быть уникальными.

Примечание

В будущем релизе, interp2 не примет смешанные комбинации векторов строки и столбца для выборки и запросит сетки. Вместо этого необходимо создать полную сетку с помощью meshgrid. В качестве альтернативы, если у вас есть большой набор данных, можно использовать griddedInterpolant вместо interp2.

Пример: [X,Y] = meshgrid(1:30,-10:10)

Типы данных: single | double

Демонстрационные значения в виде действительной или комплексной матрицы. Требования размера для V зависьте от размера X и Y:

  • Если X и Y матрицы, представляющие полную сетку (в meshgrid формат), затем V должен быть одного размера с X и Y.

  • Если X и Y векторы сетки, затем V должна быть матрица, содержащая length(Y) строки и length(X) столбцы.

Если V содержит комплексные числа, затем interp2 интерполирует действительные и мнимые части отдельно.

Пример: rand(10,10)

Типы данных: single | double
Поддержка комплексного числа: Да

Точки запроса в виде действительные скаляры, векторы, матрицы или массивы.

  • Если Xq и Yq скаляры, затем они - координаты точки единого запроса.

  • Если Xq и Yq векторы различных ориентаций, затем Xq и Yq обработаны как векторы сетки.

  • Если Xq и Yq вектора одного размера и ориентация, затем Xq и Yq обработаны как рассеянные точки на 2D пробеле.

  • Если Xq и Yq матрицы, затем они представляют любого полная сетка точек запроса (в meshgrid формат) или рассеянные точки.

  • Если Xq и Yq массивы N-D, затем они представляют рассеянные точки на 2D пробеле.

Примечание

В будущем релизе, interp2 не примет смешанные комбинации векторов строки и столбца для выборки и запросит сетки. Вместо этого необходимо создать полную сетку с помощью meshgrid. В качестве альтернативы, если у вас есть большой набор данных, можно использовать griddedInterpolant вместо interp2.

Пример: [Xq,Yq] = meshgrid((1:0.1:10),(-5:0.1:0))

Типы данных: single | double

Фактор улучшения в виде действительного, неотрицательного, целочисленного скаляра. Это значение задает число раз, чтобы неоднократно разделить интервалы усовершенствованной сетки в каждой размерности. Это приводит к 2^k-1 интерполированные точки между демонстрационными значениями.

Если k 0, затем Vq совпадает с V.

interp2(V,1) совпадает с interp2(V).

Следующий рисунок показывает размещение интерполированных значений (в красном) среди девяти демонстрационных значений (в черном цвете) для k=2.

Пример: interp2(V,2)

Типы данных: single | double

Метод интерполяции в виде одной из опций в этой таблице.

МетодОписаниеНепрерывностьКомментарии
'linear'Интерполированное значение в точке запроса основано на линейной интерполяции значений в соседних узлах решетки в каждой соответствующей размерности. Это - метод интерполяции по умолчанию.C0

  • Требует по крайней мере двух узлов решетки в каждой размерности

  • Требует большей памяти, чем 'nearest'

'nearest'Интерполированное значение в точке запроса является значением в самом близком демонстрационном узле решетки. Прерывистый

  • Требует двух узлов решетки в каждой размерности.

  • Самый быстрый расчет со скромными требованиями к памяти

'cubic'Интерполированное значение в точке запроса основано на кубичной интерполяции значений в соседних узлах решетки в каждой соответствующей размерности. Интерполяция основана на кубической свертке.C1

  • Сетка должна иметь универсальный интервал в каждой размерности, но интервал не должен быть тем же самым для всех размерностей

  • Требует по крайней мере четырех точек в каждой размерности

  • Требует большей памяти и время вычисления, чем 'linear'

'makima'Модифицированный Акима кубическая интерполяция Эрмита. Интерполированное значение в точке запроса основано на кусочно-линейной функции полиномов со степенью самое большее три оцененных использования значений соседних узлов решетки в каждой соответствующей размерности. Формула Акима изменяется, чтобы избежать перерегулирований.C1

  • Требует по крайней мере 2 точек в каждой размерности

  • Производит меньше волнистостей, чем 'spline'

  • Время вычисления обычно меньше 'spline', но требования к памяти подобны

'spline'Интерполированное значение в точке запроса основано на кубичной интерполяции значений в соседних узлах решетки в каждой соответствующей размерности. Интерполяция основана на кубическом сплайне с помощью граничных условий и условий отсутствия узла.C2

  • Требует четырех точек в каждой размерности

  • Требует большей памяти и время вычисления, чем 'cubic'

Значение функции вне области X и YВ виде действительного или комплексного скаляра. interp2 возвращает это постоянное значение для всех точек вне области X и Y.

Пример 5

Пример: 5+1i

Типы данных: single | double
Поддержка комплексного числа: Да

Выходные аргументы

свернуть все

Интерполированные значения, возвращенные как действительный или комплексный скаляр, вектор или матрица. Размер и форма Vq зависит от синтаксиса, который вы используете и, в некоторых случаях, размер и значение входных параметров.

СинтаксисыОсобые условияРазмер VqПример
interp2(X,Y,V,Xq,Yq)
interp2(V,Xq,Yq)
и изменения этих синтаксисов, которые включают method или extrapval		Xqyq скалярыСкалярsize(Vq) = [1 1] когда вы передаете Xq и Yq как скаляры.
То же самое как вышеXqyq вектора одного размера и ориентацияВектор того же размера и ориентации как Xq и YqЕсли size(Xq) = [100 1]
и size(Yq) = [100 1],
затем size(Vq) = [100 1].
То же самое как вышеXqyq векторы смешанной ориентацииМатрица, в которой количеством строк является length(Yq), и количеством столбцов является length(Xq)Если size(Xq) = [1 100]
и size(Yq) = [50 1],
затем size(Vq) = [50 100].
То же самое как вышеXqyq матрицы или массивы, одного размераМатрица или массив одного размера с Xq и YqЕсли size(Xq) = [50 25]
и size(Yq) = [50 25],
затем size(Vq) = [50 25].
interp2(V,k)
и изменения этого синтаксиса, которые включают method или extrapval		'none'

Матрица, в которой количество строк:
2^k * (size(V,1)-1)+1,

и количество столбцов:
2^k * (size(V,2)-1)+1

Если size(V) = [10 20]
и k = 2,
затем size(Vq) = [37 77].

Больше о

свернуть все

Строго Монотонный

Множество значений, которые всегда увеличиваются или уменьшаются без реверсирований. Например, последовательность, a = [2 4 6 8] является строго монотонным и увеличивается. Последовательность, b = [2 4 4 6 8] не является строго монотонным, потому что нет никакого изменения в значении между b(2) и b(3). Последовательность, c = [2 4 6 8 6] содержит реверсирование между c(4) и c(5), таким образом, это не является монотонным вообще.

Полная Сетка (в meshgrid Формате)

Для interp2, полная сетка является парой матриц, элементы которых представляют сетку точек по прямоугольной области. Одна матрица содержит x - координаты, и другая матрица содержит y - координаты. Значения в x - матрица являются строго монотонными и увеличиваются вдоль строк. Значения вдоль его столбцов являются постоянными. Значения в y - матрица являются строго монотонными и увеличиваются вдоль столбцов. Значения вдоль его строк являются постоянными. Используйте meshgrid функция, чтобы создать полную сетку, которую можно передать interp2.

Например, следующий код создает полную сетку для области, –1 ≤ x ≤ 3 и 1 ≤ y ≤ 4:

[X,Y] = meshgrid(-1:3,(1:4))
X =

    -1     0     1     2     3
    -1     0     1     2     3
    -1     0     1     2     3
    -1     0     1     2     3

Y =

     1     1     1     1     1
     2     2     2     2     2
     3     3     3     3     3
     4     4     4     4     4

Векторы сетки являются более компактным форматом, чтобы представлять сетку, чем полная сетка. Отношение между этими двумя форматами и матрицей демонстрационных значений V

Векторы сетки

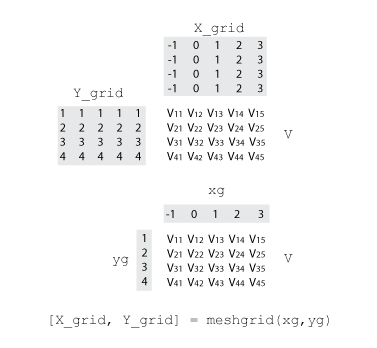
Для interp2, векторы сетки состоят из пары векторов, которые задают x - и y - координирует в сетке. Вектор-строка задает x - координаты, и вектор-столбец задает y - координаты.

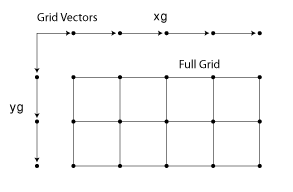
Например, следующий код создает векторы сетки, которые задают область, –1 ≤ x ≤ 3 и 1 ≤ y ≤ 4:

x = -1:3;
y = (1:4)';

Рассеянные точки

Для interp2, рассеянные точки состоят из пары массивов, которые задают набор точек, рассеянных на 2D пробеле. Один массив содержит x - координаты и другой содержат y - координаты.

Например, следующий код задает точки, (2,7), (5,3), (4,1), и (10,9):

x = [2 5; 4 10];
y = [7 3; 1 9];

Расширенные возможности

Смотрите также

| | | | | |

Представлено до R2006a

Документация MATLAB
Поддержка