Ravigneaux Gear
Планетарный механизм с двумя механизмами солнца и двумя наборами механизма планеты
- Библиотека:
Simscape / Автомобильная трансмиссия / Механизмы
Описание
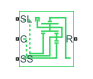
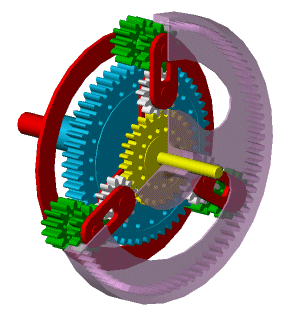
Блок Ravigneaux Gear представляет планетарную зубчатую передачу с двойными наборами механизма солнца и планеты. Два механизма солнца расположены в центре и разделяются в длину вдоль общей оси вращения. Меньший из этих механизмов затрагивает внутренний набор механизма планеты, который в свою очередь затрагивает набор механизма внешней планеты. Набор механизма внешней планеты, длина которого охватывает расстояние между двумя механизмами солнца, затрагивает и более крупный механизм солнца и кольцевой механизм.
Поставщик услуг содержит наборы механизма планеты на месте в различных радиусах. Поставщик услуг, который твердо связывает с карданным валом, может вращаться как модуль относительно солнца и звонить механизмы. Шарнирные соединения, каждый расположенный между механизмом планеты и поставщиком услуг, позволяют механизмам вращаться об их отдельных продольных осях.
Относительные скорости вращения солнца, планеты и кольцевых механизмов следуют из кинематических ограничений между ними. Для получения дополнительной информации смотрите уравнения.
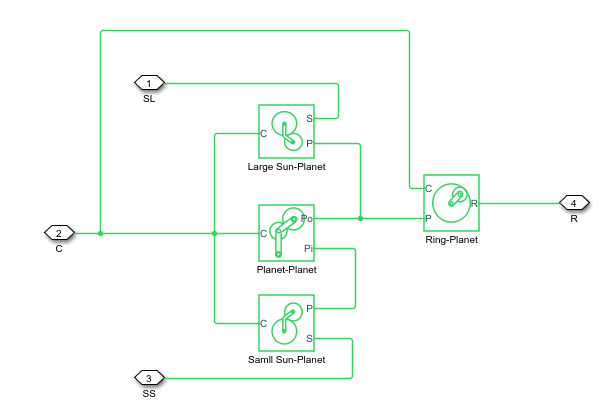
Блок моделирует механизм Ravigneaux как структурное компонентно-ориентированное на Sun-Planet, Planet-Planet и блоках Simscape™ Driveline™ Ring-Planet. Рисунок показывает блок-схему этого структурного компонента.
Чтобы увеличить точность модели механизма, можно задать свойства, такие как инерция механизма, запутывающие потери и вязкие потери. По умолчанию инерция механизма и вязкие потери приняты незначительные. Блок позволяет вам задать инерцию внутренних механизмов планеты только. Чтобы смоделировать инерцию поставщика услуг, большого солнца, небольшое солнце и кольцевые механизмы, соединяют Simscape блоки Inertia с портами C, SL, SS и R.
Тепловая модель
Можно смоделировать эффекты теплового потока и изменения температуры путем осушения дополнительного теплового порта. Чтобы осушить порт, в настройках Meshing Losses, устанавливают параметр Friction на Temperature-dependent efficiency.
Уравнения
Идеальные ограничения механизма и передаточные отношения
Механизм Ravigneaux налагает четыре кинематических и четыре геометрических ограничения на четыре связанных оси и два внутренних колеса (внутренние и внешние планеты):
Где:
rCi является радиусом внутреннего механизма поставщика услуг.
ωC является скоростью вращения механизмов поставщика услуг.
rSS является радиусом маленького механизма солнца.
ωSS является скоростью вращения маленького механизма солнца.
rPi является радиусом внутреннего механизма планеты.
ωPi является скоростью вращения внутреннего механизма планеты.
rCo является радиусом внешнего механизма поставщика услуг.
rSL является радиусом большого механизма солнца.
ωSL является скоростью вращения большого механизма солнца.
rPo является радиусом механизма внешней планеты.
ωPo является скоростью вращения механизма внешней планеты.
ωR является скоростью вращения кольцевого механизма.
Отношения звонка к солнцу:
Где:
gRSS является звонком-к-маленькому передаточное отношение солнца.
NR является количеством зубов в кольцевом механизме.
NSS является количеством зубов в маленьком механизме солнца.
gRSS является звонком-к-большому передаточное отношение солнца.
NSL является количеством зубов в большом механизме солнца.
В терминах этих передаточных отношений ключевые кинематические ограничения:
Эти шесть степеней свободы уменьшают до двух независимых степеней свободы. Пары механизма (1,2) = (LS, P), (SS, P), (P, R), и (P, P).
Предупреждение
Передаточное отношение gRSS должно строго быть больше передаточного отношения gRSL. Передаточное отношение gRSL должно строго быть больше того.
Передачи крутящего момента:
Где:
τSS является передачей крутящего момента для маленького механизма солнца.
τR является передачей крутящего момента для кольцевого механизма.
τloss(SS,R) является потерей передачи крутящего момента между маленьким механизмом солнца и кольцевым механизмом.
τSL является передачей крутящего момента для большого механизма солнца.
τloss(SL,R) является потерей передачи крутящего момента между большим механизмом солнца и кольцевым механизмом.
В идеальном случае нет никакой потери крутящего момента, которая является τloss = 0.
Неидеальные ограничения механизма и потери
В неидеальном случае, τloss ≠ 0. Для получения дополнительной информации смотрите Механизмы Модели с Потерями.
Ограничения и предположения
Механизмы приняты твердые.
Трение Кулона замедляет симуляцию. Для получения дополнительной информации смотрите, Настраивают Точность Модели.