КИХ-создание фильтра

КИХ по сравнению с БИХ-фильтрами

Цифровые фильтры с импульсной характеристикой конечной длительности (все-нуль или КИХ-фильтры) имеют и преимущества и недостатки по сравнению с фильтрами импульсной характеристики бесконечной длительности (IIR).

КИХ-фильтры имеют следующие первичные преимущества:

У них может быть точно линейная фаза.
Они всегда устойчивы.
Методы разработки обычно линейны.
Они могут быть поняты эффективно в оборудовании.
У переходных процессов запуска фильтра есть конечная длительность.

Первичный недостаток КИХ-фильтров - то, что они часто требуют, чтобы намного более высокий порядок фильтра, чем БИХ-фильтры достиг данного уровня производительности. Соответственно, задержка этих фильтров часто очень больше для равного БИХ-фильтра производительности.

КИХ-сводные данные фильтра

КИХ-фильтры

Метод создания фильтра	Описание	Функции filter
Работа с окнами	Примените окно к усеченному обратному преобразованию Фурье заданного фильтра "кирпичной стены"	`fir1`, `fir2`, `kaiserord`
Многополосный с полосами перехода	Equiripple или наименьшие квадраты приближаются по поддиапазонам частотного диапазона	`firls`, `firpm`, `firpmord`
Метод наименьших квадратов с ограничениями	Минимизируйте интегральную ошибку в квадрате по целому частотному диапазону, удовлетворяющему ограничениям максимальной погрешности	`fircls`, `fircls1`
Произвольный ответ	Произвольные ответы, включая нелинейную фазу и комплексные фильтры	`cfirpm`
Повышенный косинус	Ответ lowpass со сглаженным, синусоидальным переходом	`rcosdesign`

Линейные фильтры фазы

За исключением cfirpm, все КИХ-функции создания фильтра проектируют линейные фильтры фазы только. Коэффициенты фильтра или “касания”, таких фильтров выполняются или даже или нечетное отношение симметрии. В зависимости от этой симметрии, и на том, является ли порядок n фильтра четным или нечетный, линейный фильтр фазы (сохраненный в длине n +1 векторный b) имеет определенные свойственные ограничения на его частотную характеристику.

Линейный тип фильтра фазы	Порядок фильтра	Симметрия коэффициентов	Ответ H (f), f `=` 0	Ответ H (f), f `=` 1 (Найквист)
Тип I	Даже	даже: $b (k) = b (n + 2 - k), k = 1, ..., n + 1$	Никакое ограничение	Никакое ограничение
Тип II	Нечетный	даже: $b (k) = b (n + 2 - k), k = 1, ..., n + 1$	Никакое ограничение	H (1) `=` 0
Тип III	Даже	нечетный: $b (k) = - b (n + 2 - k), k = 1, ..., n + 1$	H (0) `=` 0	H (1) `=` 0
Введите IV	Нечетный	нечетный: $b (k) = - b (n + 2 - k), k = 1, ..., n + 1$	H (0) `=` 0	Никакое ограничение

Задержка фазы и групповая задержка КИХ-фильтров линейной фазы являются равными и постоянными по диапазону частот. Для порядка КИХ-фильтр линейной фазы n групповой задержкой является n/2, и отфильтрованный сигнал просто задержан n/2 временные шаги (и величина его преобразования Фурье масштабируется ответом величины фильтра). Это свойство сохраняет форму волны сигналов в полосе пропускания; то есть, нет никакого искажения фазы.

Функции fir1, fir2, firls, firpm, fircls, и fircls1 все КИХ-фильтры линейной фазы типа I и II проекта по умолчанию. rcosdesign проекты только фильтры типа I. Оба firls и firpm спроектируйте тип III и КИХ-фильтры линейной фазы IV, учитывая 'hilbert' или 'differentiator' флаг. cfirpm может спроектировать любой тип линейного фильтра фазы и нелинейных фильтров фазы также.

Примечание

Поскольку частотная характеристика фильтра типа II является нулем на частоте Найквиста (“высокая” частота), fir1 не проектирует тип II highpass и заграждающие фильтры. Для n с нечетным знаком в этих случаях, fir1 добавляет 1 к порядку и возвращает тип, который я фильтрую.

Метод работы с окнами

Рассмотрите идеал, или “кирпичную стену”, цифровой фильтр lowpass с частотой среза _ω0 rad/s. Этот фильтр имеет величину 1 на всех частотах с величиной меньше, чем _ω0 и величина 0 на частотах с величиной между _ω0 и π. Его последовательность импульсной характеристики h (n)

$h (n) = \frac{1}{2 π} \int_{- π}^{π} H (ω) e^{j ω n} d ω = \frac{1}{2 π} \int_{- ω_{0}}^{ω_{0}} e^{j ω n} d ω = \frac{\sin ω_{0} n}{π n}$

Этот фильтр не реализуем, поскольку его импульсная характеристика является бесконечной и непричинной. Чтобы создать импульсную характеристику конечной длительности, обрежьте его путем применения окна. Путем сохранения центрального раздела импульсной характеристики в этом усечении вы получаете КИХ-фильтр линейной фазы. Например, длина 51 фильтр с частотой среза lowpass ω ₀ из 0,4 π rad/s

b = 0.4*sinc(0.4*(-25:25));

Окно, примененное здесь, является простым прямоугольным окном. Теоремой Парсевэла это - длина 51 фильтр, который лучше всего аппроксимирует идеальный фильтр lowpass в интегрированном смысле наименьших квадратов. Следующая команда отображает частотную характеристику фильтра в FVTool:

fvtool(b,1)

Обратите внимание на то, что y - ось, показанная на рисунке ниже, находится в Величине, В квадрате. Можно установить это путем щелчка правой кнопкой по подписи по осям и выбора Magnitude Squared из меню.

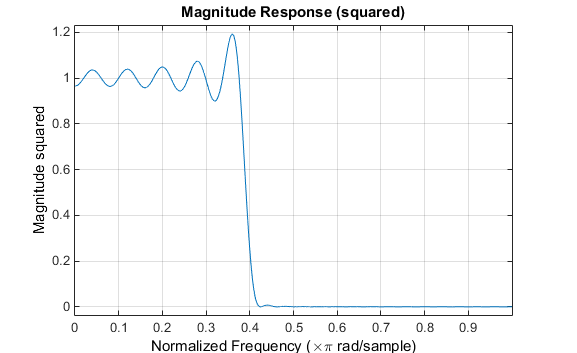
Вызов и пульсации происходит в ответе, особенно около ребра полосы. Этот “эффект Гиббса” не исчезает, когда длина фильтра увеличивается, но непрямоугольное окно уменьшает свою величину. Умножение окном в области времени вызывает свертку или сглаживающий в частотном диапазоне. Примените длину 51 Окно Хэмминга к фильтру и отобразите результат с помощью FVTool:

b = 0.4*sinc(0.4*(-25:25));
b = b.*hamming(51)';
fvtool(b,1)

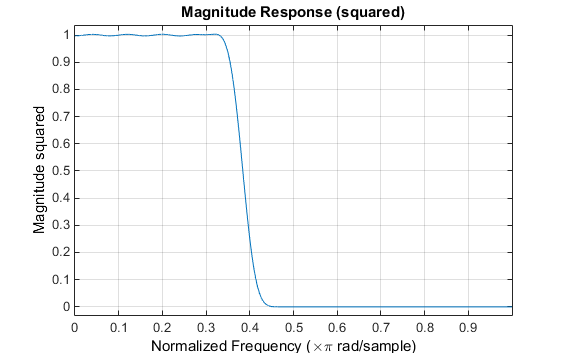
Используя Окно Хэмминга значительно уменьшает вызов. Это улучшение за счет ширины перехода (оконная версия занимает больше времени, чтобы сползать от полосы пропускания до полосы задерживания), и оптимальность (оконная версия не минимизирует интегрированную квадратичную невязку).

Функции fir1 и fir2 основаны на этом процессе работы с окнами. Учитывая порядка фильтра и описание идеального фильтра, эти функции возвращают оконное обратное преобразование Фурье того идеального фильтра. Оба используют Окно Хэмминга по умолчанию, но они принимают любую функцию окна. Смотрите Windows для обзора окон и их свойств.

Стандартное КИХ-Создание фильтра Полосы: fir1

fir1 реализует классический метод оконного линейного создания цифровых фильтров фазы FIR. Это напоминает БИХ-функции создания фильтра, в которых это формулируется, чтобы спроектировать, просачивается стандартные настройки полосы: lowpass, полоса пропускания, highpass, и bandstop.

Операторы

n = 50;
Wn = 0.4;
b = fir1(n,Wn);

создайте вектор-строку b содержа коэффициенты порядка n Hamming-оконный фильтр. Это - lowpass, КИХ-фильтр линейной фазы с частотой среза Wn. Wn номер между 0 и 1, где 1 соответствует частоте Найквиста, половина частоты дискретизации. (В отличие от других методов, здесь Wn соответствует точке на 6 дБ.) Для фильтра highpass, просто добавьте 'high' к списку параметров функции. Для полосового или заграждающего фильтра задайте Wn как двухэлементный вектор, содержащий частоты ребра полосы пропускания. Добавьте 'stop' для bandstop настройки.

b = fir1(n,Wn,window) использует окно, заданное в вектор-столбце window для проекта. Векторный window должен быть n+1 элементы долго. Если вы не задаете окно, fir1 применяет Окно Хэмминга.

Оценка порядка окна Кайзера. kaiserord функционируйте оценивает порядка фильтра, частоту среза, и бета параметр окна Кайзера должен был соответствовать данному набору технических требований. Учитывая вектор ребер диапазона частот и соответствующий вектор величин, а также максимальную допустимую пульсацию, kaiserord возвращает соответствующие входные параметры для fir1 функция.

Многополосное КИХ-Создание фильтра: fir2

fir2 функционируйте также проектирует оконные КИХ-фильтры, но с кусочной линейной частотной характеристикой произвольной формы. Это в отличие от fir1, то, которое только проектирует, просачивается стандартный lowpass, highpass, полоса пропускания и bandstop настройки.

Команды

n = 50;
f = [0 .4 .5 1];
m = [1  1  0 0];
b = fir2(n,f,m);

возвратите вектор-строку b содержа n+1 коэффициенты порядка n КИХ-фильтр, характеристики величины частоты которого совпадают с данными векторами f и mF вектор точек частоты в пределах от от 0 до 1, где 1 представляет частоту Найквиста. m вектор, содержащий заданный ответ величины в точках, заданных в f. (БИХ-дубликатом этой функции является yulewalk, который также проектирует фильтры на основе произвольных кусочных линейных ответов величины. Смотрите БИХ-Создание фильтра для деталей.)

Многополосное КИХ-создание фильтра с полосами перехода

firls и firpm функции обеспечивают более общие средние значения определения идеала заданный фильтр, чем fir1 и fir2 функции. Эти функции проектируют Гильбертовы трансформаторы, дифференциаторы и другие фильтры с нечетными симметричными коэффициентами (тип III и вводят IV линейная фаза). Они также позволяют, вы включать переход или “не заботитесь” об областях, в которых не минимизирована ошибка, и выполните зависимое взвешивание полосы минимизации.

firls функция является расширением fir1 и fir2 функции в этом это минимизирует интеграл квадрата ошибки между заданной частотной характеристикой и фактической частотной характеристикой.

firpm функционируйте реализует алгоритм Парков-McClellan, который использует алгоритм обмена Remez и Чебышевскую теорию приближения спроектировать фильтры с оптимальными подгонками между заданными и фактическими частотными характеристиками. Фильтры оптимальны в том смысле, что они минимизируют максимальную погрешность между заданной частотной характеристикой и фактической частотной характеристикой; они иногда называются минимаксными фильтрами. Фильтры, спроектированные таким образом, предоставляют equiripple поведение в своей частотной характеристике, и следовательно также известны equiripple фильтры. КИХ-алгоритм создания фильтра Парков-McClellan является, возможно, самой популярной и широко используемой КИХ-методологией создания фильтра.

Синтаксис для firls и firpm то же самое; единственной разницей являются их схемы минимизации. Следующий пример показывает, как фильтры спроектировали с firls и firpm отразите эти различные схемы.

Базовые конфигурации

Режим по умолчанию операции firls и firpm должен спроектировать тип I или тип II линейные фильтры фазы, в зависимости от того, является ли порядок, который вы хотите, четным или нечетный, соответственно. Пример lowpass с аппроксимированной амплитудой 1 от 0 до 0,4 Гц и аппроксимированной амплитудой 0 от 0,5 до 1,0 Гц

n = 20;                    % Filter order
f = [0 0.4 0.5 1];         % Frequency band edges
a = [1  1  0 0];           % Amplitudes
b = firpm(n,f,a);

От 0,4 до 0,5 Гц, firpm не выполняет ошибочной минимизации; это - полоса перехода, или “не заботятся” об области. Полоса перехода минимизирует ошибку больше в полосах, о которых вы действительно заботитесь о, за счет более медленного уровня перехода. Таким образом эти типы фильтров имеют свойственный компромисс, похожий на КИХ-проект работой с окнами.

Чтобы сравнить наименьшие квадраты с equiripple созданием фильтра, используйте firls создать подобный фильтр. Ввод

bb = firls(n,f,a);

и сравните их частотные характеристики с помощью FVTool:

fvtool(b,1,bb,1)

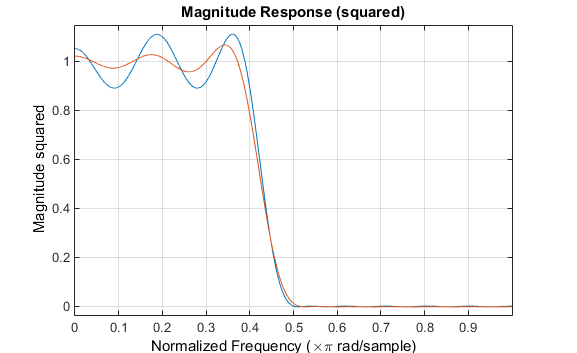
Фильтр спроектирован с firpm выставки equiripple поведение. Также обратите внимание что firls фильтр имеет лучший ответ по большей части полосы пропускания и полосы задерживания, но в ребрах полосы (f= 0.4 и f= 0.5 ), ответ еще дальше от идеала, чем firpm фильтр. Это показывает что firpm максимальная погрешность фильтра по полосе пропускания и полосе задерживания меньше и, на самом деле, это является самым маленьким для этой настройки ребра полосы и длины фильтра.

Думайте о диапазонах частот как о линиях на коротких интервалах частоты. firpm и firls используйте эту схему представлять любую кусочную линейную функцию частотной характеристики с любыми полосами перехода. firls и firpm спроектируйте lowpass, highpass, полосу пропускания и заграждающие фильтры; полосовой пример

f = [0 0.3  0.4  0.7  0.8  1];   % Band edges in pairs
a = [0  0    1    1    0   0];   % Bandpass filter amplitude

Технически, они f и a векторы задают пять полос:

Две полосы задерживания, от 0,0 до 0,3 и от 0,8 до 1,0
Полоса пропускания от 0,4 до 0,7
Две полосы перехода, от 0,3 до 0,4 и от 0,7 до 0,8

Пример highpass и заграждающие фильтры

f = [0 0.7  0.8  1];            % Band edges in pairs
a = [0  0    1   1];            % Highpass filter amplitude
f = [0 0.3  0.4  0.5  0.8  1];  % Band edges in pairs
a = [1  1    0    0    1   1];  % Bandstop filter amplitude

Пример многополосный полосовой фильтр

f = [0 0.1 0.15 0.25 0.3 0.4 0.45 0.55 0.6 0.7 0.75 0.85 0.9 1];
a = [1  1   0    0    1   1   0    0    1   1   0    0    1  1];

Другая возможность является фильтром, который имеет как область перехода линия, соединяющая полосу пропускания с полосой задерживания; это может помочь управлять “безудержным” ответом величины в широких областях перехода:

f = [0 0.4 0.42 0.48 0.5  1];
a = [1 1 0.8 0.2 0 0];   % Passband, linear transition, 
                         %  stopband

Вектор веса

Оба firls и firpm позвольте вам делать более или менее акцент на минимизацию ошибки в определенных диапазонах частот относительно других. Для этого задайте вектор веса после частоты и амплитудные векторы. Пример lowpass equiripple фильтр с в 10 раз меньшим количеством пульсации в полосе задерживания, чем полоса пропускания

n = 20;              % Filter order
f = [0 0.4 0.5 1];   % Frequency band edges
a = [1  1   0  0];   % Amplitudes
w = [1 10];          % Weight vector
b = firpm(n,f,a,w);

Легальный вектор веса всегда является половиной длины f и a векторы; должен быть точно один вес на полосу.

Антисимметричные Фильтры / Гильбертовы Трансформаторы

Когда названо запаздывающим 'h' или 'Hilbert' опция, firpm и firls спроектируйте КИХ-фильтры с нечетной симметрией, то есть, тип III (для даже порядка) или введите IV (для нечетного порядка) линейные фильтры фазы. Идеальный Гильбертов трансформатор имеет это свойство антисимметрии и амплитуду 1 через целый частотный диапазон. Попробуйте следующие аппроксимированные Гильбертовы трансформаторы и постройте их использующий FVTool:

b = firpm(21,[0.05 1],[1 1],'h');       % Highpass Hilbert
bb = firpm(20,[0.05 0.95],[1 1],'h');   % Bandpass Hilbert
fvtool(b,1,bb,1)

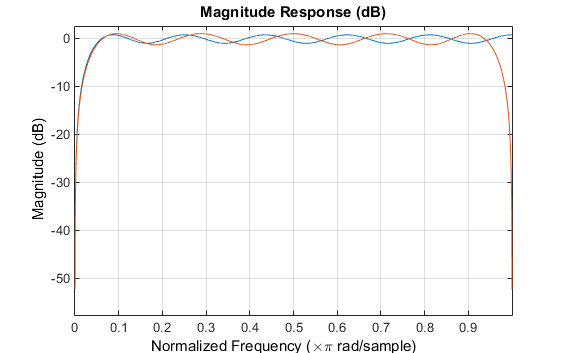
Можно найти задержанное преобразование Гильберта x сигнала путем передачи его через эти фильтры.

fs = 1000;            % Sampling frequency
t = (0:1/fs:2)';      % Two second time vector
x = sin(2*pi*300*t);  % 300 Hz sine wave example signal
xh = filter(bb,1,x);  % Hilbert transform of x

Аналитический сигнал, соответствующий x комплексный сигнал, который имеет x как его действительная часть и преобразование Гильберта x как его мнимая часть. Для этого КИХ-метода (альтернатива hilbert функция), необходимо задержать x наполовину порядок фильтра, чтобы создать аналитический сигнал:

xd = [zeros(10,1); x(1:length(x)-10)];	    % Delay 10 samples
xa = xd + j*xh;                            % Analytic signal

Этот метод не работает непосредственно на фильтры нечетного порядка, которые требуют задержки нецелого числа. В этом случае, hilbert функция, описанная в преобразовании Гильберта, оценивает аналитический сигнал. В качестве альтернативы используйте resample функция, чтобы задержать сигнал количеством нецелого числа выборок.

Дифференциаторы

Дифференцирование сигнала во временном интервале эквивалентно умножению преобразования Фурье сигнала мнимой функцией пандуса. Таким образом, чтобы дифференцировать сигнал, передайте его через фильтр, который имеет ответ H (ω) = j ω. Аппроксимируйте идеальный дифференциатор (задержкой) использование firpm или firls с 'd' или 'differentiator' опция:

b = firpm(21,[0 1],[0 pi],'d');

Для фильтра типа III полоса дифференцирования должна не дойти до частоты Найквиста, и амплитудный вектор должен отразить что изменение, чтобы гарантировать правильный наклон:

bb = firpm(20,[0 0.9],[0 0.9*pi],'d');

В 'd' режим, firpm взвешивает ошибку 1/ω в ненулевых амплитудных полосах, чтобы минимизировать максимальную относительную погрешность. firls взвешивает ошибку (1/ω) ² в ненулевых амплитудных полосах в 'd' режим.

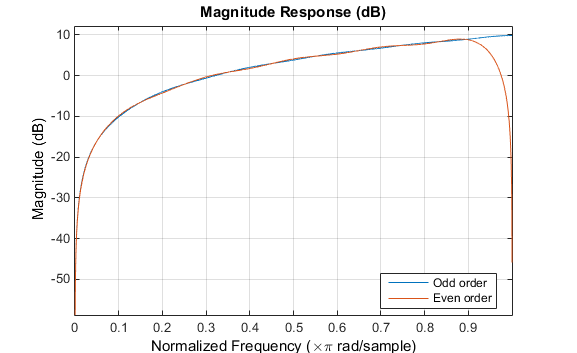
Следующие графики показывают ответы величины для дифференциаторов выше.

fvtool(b,1,bb,1)
legend('Odd order','Even order','Location','best')

КИХ-создание фильтра метода наименьших квадратов с ограничениями

КИХ-функции создания фильтра Метода наименьших квадратов с ограничениями (CLS) реализуют метод, который позволяет вам спроектировать КИХ-фильтры, явным образом не задавая полосы перехода для ответа величины. Способность не использовать спецификацию полос перехода полезна в нескольких ситуациях. Например, не может быть ясно, где твердо заданная полоса перехода должна появиться, если шумовая и информация сигнала появляется вместе в том же диапазоне частот. Точно так же это может быть целесообразно не использовать спецификацию полос перехода, если они, кажется, только управляют результатами Явлений Гиббса, которые появляются в ответе фильтра. См. Selesnick, Ленга и Берруса [2] для обсуждения этого метода.

Вместо того, чтобы задать полосы пропускания, полосы задерживания и области перехода, метод CLS принимает частоту среза (для highpass, lowpass, полосы пропускания или bandstop случаев), или полоса пропускания и ребра полосы задерживания (для многополосных случаев), для ответа, который вы задаете. Таким образом метод CLS задает области перехода неявно, а не явным образом.

Ключевая возможность метода CLS - то, что он позволяет вам задать верхние и более низкие пороги, которые содержат максимальную допустимую пульсацию в ответе величины. Учитывая это ограничение, метод применяет ошибочный метод минимизации наименьшего квадрата по частотному диапазону ответа фильтра, вместо по определенным полосам. Ошибочная минимизация включает любые области разрыва в идеале, ответе "кирпичной стены". Дополнительная выгода - то, что метод позволяет вам задать произвольно маленький peaks, следующий из Явления Гиббса.

Существует две функции тулбокса, которые реализуют этот метод проектирования.

Описание	Функция
Ограниченный наименьший квадрат многополосное КИХ-создание фильтра	`fircls`
Ограниченное создание фильтра наименьшего квадрата для lowpass и highpass линейных фильтров фазы	`fircls1`

Для получения дополнительной информации на синтаксисе вызова для этих функций, см. их ссылочные описания в Ссылке на функцию.

Основной Lowpass и создание фильтра CLS Highpass

Самые основные из CLS проектируют функции, fircls1, использование этот метод, чтобы спроектировать lowpass и highpass КИХ-фильтры. Как пример, считайте разработку фильтра с импульсной характеристикой порядка 61 и частотой среза 0,3 (нормированной). Далее, задайте верхние и нижние границы, которые ограничивают процесс проектирования как:

Максимальное отклонение полосы пропускания от 1 (неравномерность в полосе пропускания) 0,02.
Максимальное отклонение полосы задерживания от 0 (пульсация полосы задерживания) 0,008.

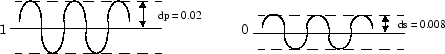
Приблизиться к этой проблеме проектирования с помощью fircls1, используйте следующие команды:

n = 61;
wo = 0.3;
dp = 0.02;	
ds = 0.008;
h = fircls1(n,wo,dp,ds);
fvtool(h,1)

Обратите внимание на то, что y - ось, показанная ниже, находится в Величине, В квадрате. Можно установить это путем щелчка правой кнопкой по подписи по осям и выбора Magnitude Squared из меню.

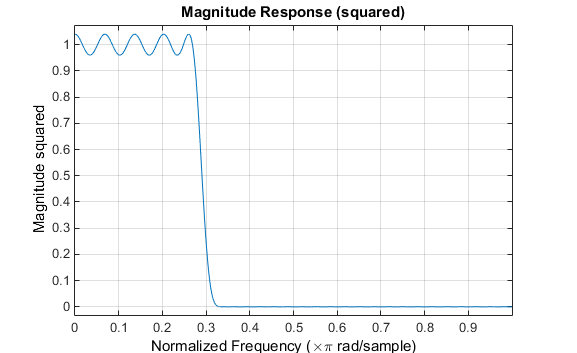
Многополосное создание фильтра CLS

fircls использует тот же метод, чтобы спроектировать КИХ-фильтры с заданным кусочным постоянным ответом величины. В этом случае можно задать вектор ребер полосы и соответствующий вектор амплитуд полосы. Кроме того, можно задать максимальную сумму пульсации для каждой полосы.

Например, примите, что технические требования для фильтра призывают:

От 0 до 0,3 (нормированный): амплитуда 0, верхняя граница 0.005, нижняя граница –0.005
От 0,3 до 0,5: амплитуда 0.5, верхняя граница 0.51, нижняя граница 0.49
От 0,5 до 0,7: амплитуда 0, верхняя граница 0.03, нижняя граница –0.03
От 0,7 до 0,9: амплитуда 1, верхняя граница 1.02, нижняя граница 0.98
От 0,9 до 1: амплитуда 0, верхняя граница 0.05, нижняя граница –0.05

Спроектируйте фильтр CLS с порядком 129 импульсной характеристики, который выполняет этим техническим требованиям:

n = 129;
f = [0 0.3 0.5 0.7 0.9 1];
a = [0 0.5 0 1 0];
up = [0.005 0.51 0.03 1.02 0.05];
lo = [-0.005 0.49 -0.03 0.98 -0.05];
h = fircls(n,f,a,up,lo);
fvtool(h,1)

Взвешенное создание фильтра CLS

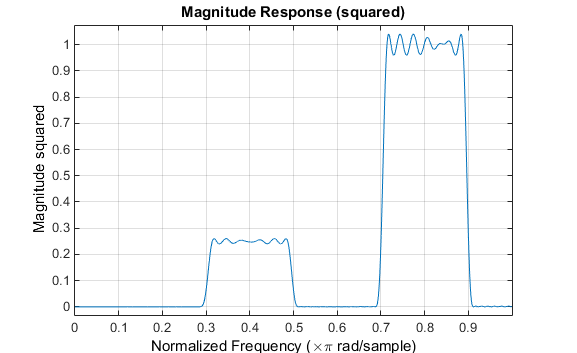
Взвешенное создание фильтра CLS позволяет вам спроектировать lowpass или highpass КИХ-фильтры с относительным взвешиванием ошибочной минимизации в каждой полосе. fircls1 функция позволяет вам задать полосу пропускания и ребра полосы задерживания для функции взвешивания наименьших квадратов, а также постоянный k это задает отношение полосы задерживания к взвешиванию полосы пропускания.

Например, рассмотрите технические требования, которые призывают к КИХ-фильтру с порядком импульсной характеристики 55 и частотой среза 0,3 (нормированный). Также примите максимальную допустимую неравномерность в полосе пропускания 0,02 и максимальную допустимую пульсацию полосы задерживания 0,004. Кроме того, добавьте требования взвешивания:

Ребро полосы пропускания для функции веса 0,28 (нормированный)
Ребро полосы задерживания для функции веса 0,32
Ошибочная минимизация веса в 10 раз больше в полосе задерживания, чем в полосе пропускания

Приблизиться к этому использованию fircls1Ввод

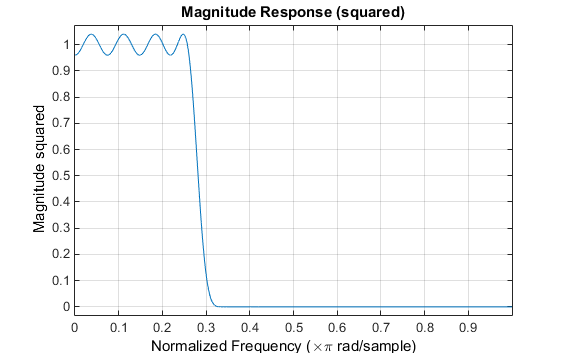
n = 55;
wo = 0.3;
dp = 0.02;
ds = 0.004;
wp = 0.28;
ws = 0.32;
k = 10;
h = fircls1(n,wo,dp,ds,wp,ws,k);
fvtool(h,1)

Создание фильтра произвольного ответа

cfirpm функция создания фильтра обеспечивает инструмент для разработки КИХ-фильтров с произвольными комплексными ответами. Это отличается от других функций создания фильтра в том, как частотная характеристика фильтра задана: это принимает имя функции, которая возвращает ответ фильтра, вычисленный по сетке частот. Эта возможность делает cfirpm очень универсальный и мощный метод для создания фильтра.

Этот метод проектирования может использоваться, чтобы произвести КИХ-фильтры нелинейной фазы, асимметричные фильтры частотной характеристики (с комплексными коэффициентами) или больше симметричных фильтров с пользовательскими частотными характеристиками.

Алгоритм проекта оптимизирует Чебышева (или минимакс) ошибка расширенный Remez-обменный алгоритм для первоначальной оценки. Если этому обменному методу не удается получить оптимальный фильтр, алгоритм переключается на алгоритм спуска подъема, который вступает во владение, чтобы закончить сходимость к оптимальному решению.

Многополосное создание фильтра

Рассмотрите многополосный фильтр со следующими специальными характеристиками частотного диапазона.

Полоса	Амплитуда	Взвешивание оптимизации
[–1 –0.5]	[5 1]	1
[–0.4 +0.3]	[2 2]	10
[+0.4 +0.8]	[2 1]	5

Линейная фаза многополосный фильтр может быть создана с использованием предопределенная функция частотной характеристики multiband, можно следующим образом:

b = cfirpm(38, [-1 -0.5 -0.4 0.3 0.4 0.8], ...
               {'multiband', [5 1 2 2 2 1]}, [1 10 5]);

Для конкретного случая многополосного фильтра мы можем использовать краткое обозначение создания фильтра, похожее на синтаксис для firpm:

b = cfirpm(38,[-1 -0.5 -0.4 0.3 0.4 0.8], ...
              [5 1 2 2 2 1], [1 10 5]);

Как с firpm, вектор ребер полосы передается cfirpm. Этот вектор задает диапазоны частот, по которым выполняется оптимизация; обратите внимание, что существует две полосы перехода, от –0.5 до –0.4 и от 0,3 до 0,4.

В любом случае частотная характеристика получена и построила линейную шкалу использования в FVTool:

fvtool(b,1)

Обратите внимание на то, что областью значений данных, показанных ниже, является (-pi,pi).

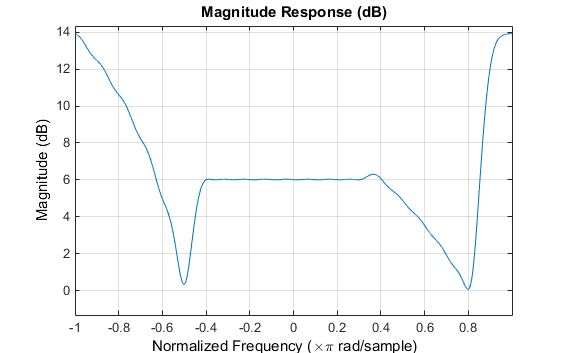
Ответ фильтра для этого многополосного фильтра является комплексным, который ожидается из-за асимметрии в частотном диапазоне. Импульсную характеристику, которую можно выбрать из панели инструментов FVTool, показывают ниже.

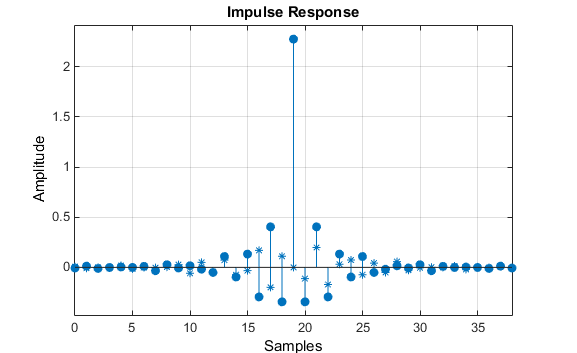
Создание фильтра с уменьшаемой задержкой

Рассмотрите проект фильтра lowpass с 62 касаниями с сокращением хэлф-Найквиста. Если мы задаем отрицательное значение смещения к lowpass функция создания фильтра, смещение групповой задержки для проекта значительно меньше, который получил для стандартного проекта линейной фазы. Это создание фильтра может быть вычислено можно следующим образом:

b = cfirpm(61,[0 0.5 0.55 1],{'lowpass',-16});

Получившийся ответ величины

fvtool(b,1)

y - ось находится в Величине, В квадрате, который можно установить путем щелчка правой кнопкой по подписи по осям и выбора Magnitude Squared из меню.

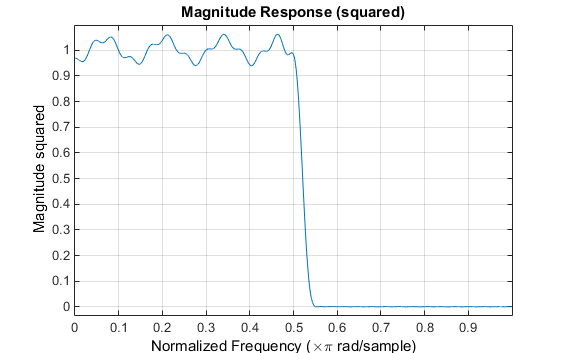
Групповая задержка фильтра показывает, что смещение уменьшалось от N/2 к N/2-16 (т.е. от 30.5 к 14.5). Теперь однако групповая задержка является более не плоской в области полосы пропускания. Чтобы создать этот график, нажмите кнопку Group Delay Response на панели инструментов.

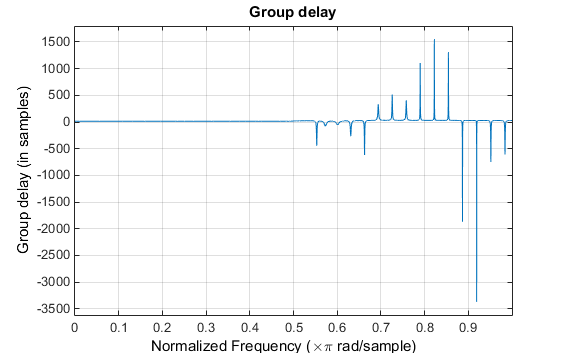
Если мы сравниваем этот фильтр нелинейной фазы с фильтром линейной фазы, который имеет точно 14,5 выборок групповой задержки, получившийся фильтр имеет порядок 2*14.5, или 29. Используя b = cfirpm(29,[0 0.5 0.55 1],'lowpass'), пульсация полосы пропускания и полосы задерживания намного больше для фильтра порядка 29. Эти сравнения могут помочь вам в решении, какой фильтр более подходит для определенного приложения.

Документация