Первичное преимущество БИХ-фильтров по КИХ-фильтрам состоит в том, что они обычно соответствуют данному набору технических требований с намного более низким порядком фильтра, чем соответствующий КИХ-фильтр. Несмотря на то, что БИХ-фильтры имеют нелинейную фазу, обработка данных в MATLAB обычно выполняется “оффлайн”, то есть, целая последовательность данных доступна до фильтрации. Это допускает непричинный, подход фильтрации нулевой фазы (через filtfilt функция), который устраняет нелинейное искажение фазы БИХ-фильтра.
Классические БИХ-фильтры, Баттерворт, Чебышевские Типы I и II, эллиптические, и функция Бесселя, все аппроксимируют идеальный фильтр “кирпичной стены” по-разному.
Этот тулбокс обеспечивает, функции, чтобы создать все эти типы классического БИХ просачивается и аналоговые и цифровые области (кроме функции Бесселя, для которой только аналоговый случай поддерживается), и в lowpass, highpass, полосе пропускания и bandstop настройках. Для большинства типов фильтра можно также найти самого низкого порядка фильтра, который соответствует данной спецификации фильтра в терминах полосы пропускания и затухания в полосе задерживания и ширины (ширин) перехода.
Прямое создание фильтра функционирует yulewalk находит фильтр с ответом величины, аппроксимирующим заданную функцию частотной характеристики. Это - один способ создать многополосный полосовой фильтр.
Можно также использовать параметрическое моделирование или функции системы идентификации, чтобы спроектировать БИХ-фильтры. Эти функции обсуждены в Параметрическом моделировании.
Обобщенный Баттерворт проектирует функциональный maxflat обсужден в разделе Generalized Butterworth Filter Design.
Следующая таблица обобщает различные методы фильтра в тулбоксе и приводит функции, доступные, чтобы реализовать эти методы.
Тулбокс фильтрует методы и доступные функции
| Отфильтруйте метод | Описание | Функции filter |
|---|---|---|
Аналоговое прототипирование | Используя полюса и нули классического lowpass прототип просачивается непрерывная область (Лапласа), получает цифровой фильтр посредством преобразования частоты и фильтрует дискретизацию. | Полные функции проекта: besself, butter, cheby1, cheby2, ellipФункции оценки порядка: buttord, cheb1ord, cheb2ord, ellipordАналог lowpass моделирует функции: besselap, buttap, cheb1ap, cheb2ap, ellipapФункции преобразования частоты: lp2bp, lp2bs, lp2hp, lp2lpФункции дискретизации фильтра: bilinear, impinvar |
Прямой проект | Спроектируйте цифровой фильтр непосредственно в дискретном временном интервале путем аппроксимации кусочного линейного ответа величины. | |
Обобщенный проект Баттерворта | Спроектируйте Фильтры Баттерворта lowpass с большим количеством нулей, чем полюса. | |
Параметрическое моделирование | Найдите цифровой фильтр, который аппроксимирует предписанное время или ответ частотного диапазона. (См. документацию System Identification Toolbox™ для обширного набора инструментов параметрического моделирования.) | Функции моделирования временного интервала: lpc, prony, stmcbФункции моделирования частотного диапазона: invfreqs, invfreqz |
Основной БИХ-метод создания цифровых фильтров, который обеспечивает этот тулбокс, основан на преобразовании классических аналоговых фильтров lowpass к их цифровым эквивалентам. Следующие разделы описывают, как спроектировать фильтры и обобщить характеристики поддерживаемых типов фильтра. Смотрите Специальные Темы в БИХ-Создании фильтра для подробных шагов на процессе создания фильтра.
Можно легко создать фильтр любого порядка с lowpass, highpass, полосой пропускания или bandstop настройкой с помощью функций создания фильтра.
Функции создания фильтра
Отфильтруйте тип | Функция проекта |
|---|---|
Функция Бесселя (только аналог) |
|
Баттерворт |
|
Чебышевский тип I |
|
Чебышевский тип II |
|
Эллиптический |
|
По умолчанию каждая из этих функций возвращает фильтр lowpass; необходимо задать только частоту среза, которую вы хотите, Wn, в нормированных единицах, таким образом, что частота Найквиста составляет 1 Гц). Для фильтра highpass добавьте 'high' к списку параметров функции. Для полосового или заграждающего фильтра задайте Wn как двухэлементный вектор, содержащий частоты ребра полосы пропускания. Добавьте 'stop' для bandstop настройки.
Вот некоторые цифровые фильтры в качестве примера:
[b,a] = butter(5,0.4); % Lowpass Butterworth [b,a] = cheby1(4,1,[0.4 0.7]); % Bandpass Chebyshev Type I [b,a] = cheby2(6,60,0.8,'high'); % Highpass Chebyshev Type II [b,a] = ellip(3,1,60,[0.4 0.7],'stop'); % Bandstop elliptic
Чтобы спроектировать аналоговый фильтр, возможно, для симуляции, используют запаздывающий 's' и задайте частоты среза в rad/s:
[b,a] = butter(5,0.4,'s'); % Analog Butterworth filter
Все функции создания фильтра возвращают фильтр в передаточной функции, нулях, полюсах и усилении или представлении модели линейной системы пространства состояний, в зависимости от того, сколько выходных аргументов присутствует. В общем случае необходимо избегать использования формы передаточной функции, потому что могут произойти числовые проблемы, вызванные ошибками округления. Вместо этого используйте форму нулей, полюсов и усиления, которую можно преобразовать в форму секции второго порядка (SOS) с помощью zp2sos и затем используйте форму SOS, чтобы анализировать или реализовать ваш фильтр.
Все классические БИХ фильтры lowpass плохо обусловлены для чрезвычайно низких частот среза. Поэтому вместо того, чтобы проектировать БИХ-фильтр lowpass с очень узкой полосой пропускания, может быть лучше спроектировать более широкую полосу пропускания и десятикратно уменьшить входной сигнал.
Этот тулбокс обеспечивает функции выбора порядка, которые вычисляют минимального порядка фильтра, который соответствует данному набору требований.
Отфильтруйте тип | Закажите функцию оценки |
|---|---|
Баттерворт |
|
Чебышевский тип I |
|
Чебышевский тип II |
|
Эллиптический |
|
Они полезны в сочетании с функциями создания фильтра. Предположим, что вы хотите полосовой фильтр с полосой пропускания от 1 000 до 2 000 Гц, полосы задерживания, запускающиеся на расстоянии в 500 Гц с обеих сторон, частота дискретизации на 10 кГц, самое большее 1 дБ неравномерности в полосе пропускания и по крайней мере 60 дБ затухания в полосе задерживания. Можно выполнить этим техническим требованиям при помощи butter функция можно следующим образом.
[n,Wn] = buttord([1000 2000]/5000,[500 2500]/5000,1,60) [b,a] = butter(n,Wn);
n =
12
Wn =
0.1951 0.4080Эллиптическим фильтром, который удовлетворяет те же требования, дают
[n,Wn] = ellipord([1000 2000]/5000,[500 2500]/5000,1,60) [b,a] = ellip(n,1,60,Wn);
n =
5
Wn =
0.2000 0.4000Эти функции также работают с другими стандартными настройками полосы, а также для аналоговых фильтров.
Тулбокс обеспечивает пять различных типов классических БИХ-фильтров, каждый оптимальный в некотором роде. Этот раздел показывает основную аналоговую прототипную форму для каждого и обобщает главные характеристики.
Фильтр Баттерворта предоставляет лучшее приближение Ряда Тейлора идеальному ответу фильтра lowpass на аналоговых частотах Ω = 0 и Ω = ∞; для любого порядка N ответ величины в квадрате имеет 2N – 1 нулевая производная в этих местоположениях (максимально плоский в Ω = 0 и Ω = ∞). Ответ является монотонным в целом, уменьшаясь гладко с Ω = 0 к Ω = ∞. в Ω = 1.
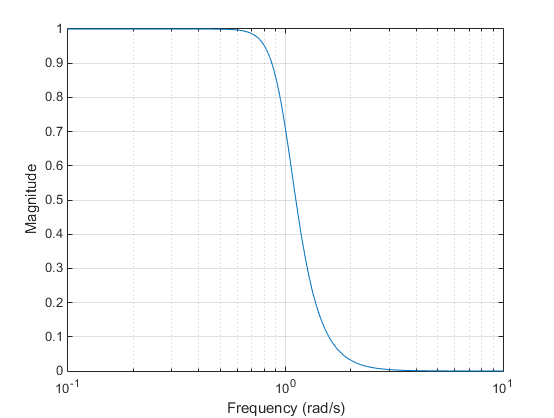
Фильтр Чебышевский Тип 1 минимизирует абсолютную разность между идеальной и фактической частотной характеристикой по целой полосе пропускания путем слияния равной пульсации Rp дБ в полосе пропускания. Ответ полосы задерживания является максимально плоским. Переход от полосы пропускания до полосы задерживания более быстр, чем для Фильтра Баттерворта. в Ω = 1.
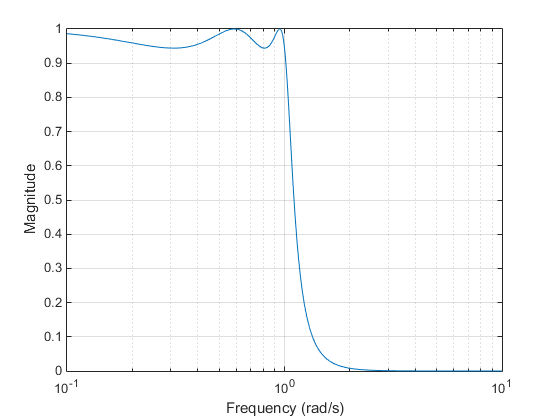
Чебышевский фильтр Типа II минимизирует абсолютную разность между идеальной и фактической частотной характеристикой по целой полосе задерживания путем слияния равной пульсации Rs дБ в полосе задерживания. Ответ полосы пропускания является максимально плоским.
Полоса задерживания не приближается к нулю так же быстро как тип , который я фильтрую (и не приближается к нулю вообще для четного порядка фильтра n). Отсутствие пульсации в полосе пропускания, однако, часто является важным преимуществом. в Ω = 1.
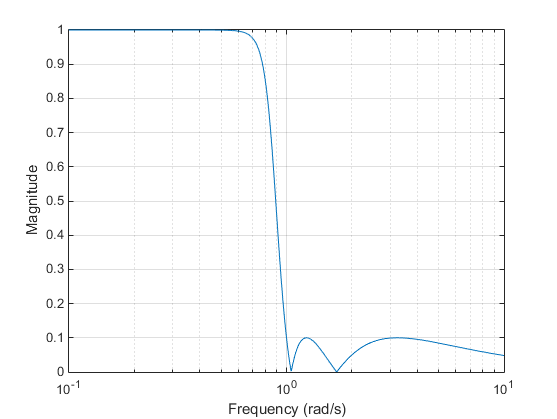
Эллиптические фильтры являются equiripple и в полосе пропускания и в полосе задерживания. Они обычно удовлетворяют требования фильтра с самым низкоуровневым из любого поддерживаемого типа фильтра. Учитывая порядка фильтра n, неравномерность в полосе пропускания Rp в децибелах и полосе задерживания слегка колеблются Rs в децибелах эллиптические фильтры минимизируют ширину перехода. в Ω = 1.
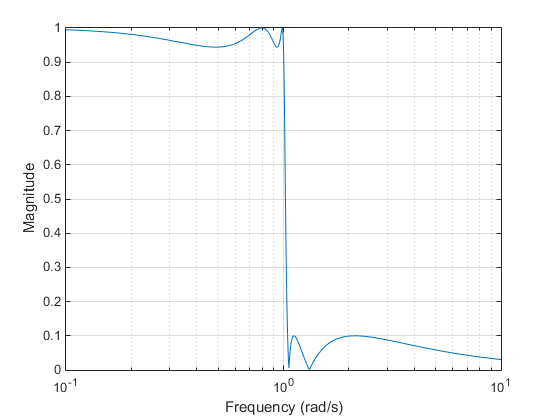
Аналоговая функция Бесселя фильтры lowpass имеют максимально плоскую групповую задержку на нулевой частоте и сохраняют почти постоянную групповую задержку через целую полосу пропускания. Фильтрованные сигналы поэтому обеспечивают свой waveshapes в частотном диапазоне полосы пропускания. Когда аналоговая функция Бесселя, фильтр lowpass преобразован в цифровой посредством отображения частоты, это больше, имеет это максимально плоское свойство. Signal Processing Toolbox™ поддерживает только аналоговый случай для полной функции проекта фильтра Бесселя.
Фильтры Бесселя обычно требуют более высокого порядка фильтра, чем другие фильтры для удовлетворительного затухания в полосе задерживания. в Ω = 1 и уменьшения, когда увеличивается порядок фильтра n.
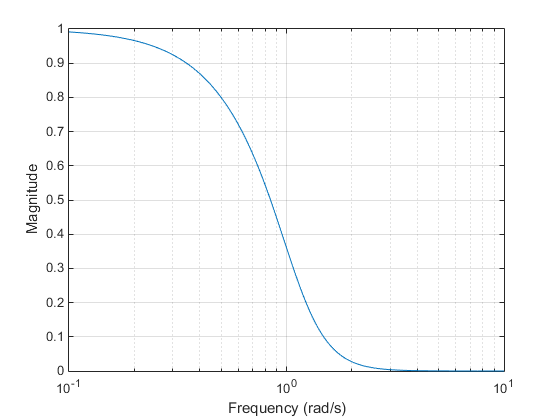
Фильтры lowpass, показанные выше, были созданы с аналоговыми прототипными функциями besselap, buttap, cheb1ap, cheb2ap, и ellipap. Эти функции находят нули, полюса и усиление nаналоговый фильтр th-порядка соответствующего типа с частотой среза 1 рад/с. Полные функции создания фильтра (besself, butter, cheby1, cheby2, и ellip) вызовите функции прототипирования как первый шаг в процессе проектирования. Смотрите Специальные Темы в БИХ-Создании фильтра для деталей.
Чтобы создать подобные графики, используйте n= 5 и, по мере необходимости, Rp= 0.5 и Rs= 20 . Например, чтобы создать эллиптический график фильтра:
[z,p,k] = ellipap(5,0.5,20); w = logspace(-1,1,1000); h = freqs(k*poly(z),poly(p),w); semilogx(w,abs(h)), grid xlabel('Frequency (rad/s)') ylabel('Magnitude')
Этот тулбокс использует термин прямые методы описать методы для БИХ-проекта, которые находят фильтр на основе технических требований в дискретной области. В отличие от аналогового метода прототипирования, прямые методы разработки не ограничиваются к стандартному lowpass, highpass, полосе пропускания или bandstop настройкам. Скорее эти функции проектируют фильтры с произвольным, возможно, многополосная, частотная характеристика. В этом разделе рассматриваются yulewalk функция, которая предназначается специально для создания фильтра; Параметрическое моделирование обсуждает другие методы, которые могут также быть рассмотрены прямыми, такие как метод Прони, Линейное предсказание, метод Steiglitz-McBride и обратный проект частоты.
yulewalk функционируйте проектирует рекурсивные БИХ-цифровые фильтры путем подбора кривой заданной частотной характеристике. yulewalkназовите отражает его метод для нахождения коэффициентов знаменателя фильтра: это находит, что обратный БПФ идеала задал ответ в квадрате величиной и решает модифицированные уравнения Уокера Рождества с помощью получившихся выборок автокорреляционной функции. Оператор
[b,a] = yulewalk(n,f,m)
возвращает векторы-строки b и a содержа n+1 числитель и коэффициенты знаменателя nБИХ th-порядка фильтруют, чьи характеристики величины частоты аппроксимируют данных в векторах f и mF вектор точек частоты в пределах от от 0 до 1, где 1 представляет частоту Найквиста. m вектор, содержащий заданный ответ величины в точках в fF и m может описать любой кусочный линейный ответ величины формы, включая многополосный ответ. КИХ-дубликатом этой функции является fir2, который также проектирует фильтр на основе произвольного кусочного линейного ответа величины. Смотрите КИХ-Создание фильтра для деталей.
Обратите внимание на то, что yulewalk не принимает информацию о фазе, и никакие операторы не сделаны об оптимальности получившегося фильтра.
Спроектируйте многополосный фильтр с yulewalk и постройте заданную и фактическую частотную характеристику:
m = [0 0 1 1 0 0 1 1 0 0]; f = [0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 1]; [b,a] = yulewalk(10,f,m); [h,w] = freqz(b,a,128) plot(f,m,w/pi,abs(h))
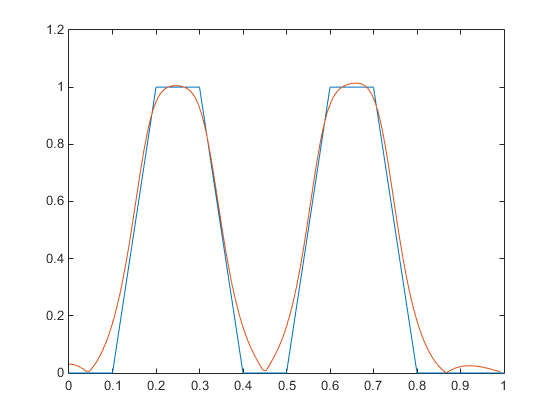
Функция тулбокса maxflat позволяет вам спроектировать обобщенные Фильтры Баттерворта, то есть, Фильтры Баттерворта с отличающимися количествами нулей и полюсов. Это желательно в некоторых реализациях, где полюса являются более дорогими в вычислительном отношении, чем нули. maxflat точно так же, как butter функция, за исключением того, что это можно задать два порядка (один для числителя и один для знаменателя) вместо всего один. Эти фильтры являются максимально плоскими. Это означает, что получившийся фильтр оптимален для любого числителя и порядков знаменателя с максимальным количеством производных в 0 и частота Найквиста ω = π оба набора к 0.
Например, когда два порядка являются тем же самым, maxflat совпадает с butter:
[b,a] = maxflat(3,3,0.25)
b =
0.0317 0.0951 0.0951 0.0317
a =
1.0000 -1.4590 0.9104 -0.1978[b,a] = butter(3,0.25)
b =
0.0317 0.0951 0.0951 0.0317
a =
1.0000 -1.4590 0.9104 -0.1978Однако maxflat более универсально, потому что это позволяет вам проектировать фильтр с большим количеством нулей, чем полюса:
[b,a] = maxflat(3,1,0.25)
b =
0.0950 0.2849 0.2849 0.0950
a =
1.0000 -0.2402Третий вход к maxflat частота на уровне половинной мощности, частота между 0 и 1 с ответом величины .
Можно также спроектировать линейные фильтры фазы, которые имеют максимально плоское свойство с помощью 'sym' опция:
maxflat(4,'sym',0.3)ans =
0.0331 0.2500 0.4337 0.2500 0.0331Для полных деталей maxflat алгоритм, смотрите Selesnick и Burrus [2].