LPV System

Симулируйте системы Линейного варьирования параметра (LPV)

Описание

Представляйте и симулируйте системы Линейного варьирования параметра (LPV) в Simulink^®. Блок также поддерживает генерацию кода.

linear parameter-varying (LPV), система является линейной моделью в пространстве состояний, движущие силы которой варьируются как функция определенных изменяющихся во времени параметров под названием scheduling parameters. В MATLAB^® модель LPV представлена в форме пространства состояний с помощью коэффициентов, которые являются зависимым параметра.

Математически, система LPV представлена как:

\begin{array}{l} d x (t) = A (p) x (t) + B (p) u (t) \\ y (t) = C (p) x (t) + D (p) u (t) \\ x (0) = x_{0} \end{array}

(1)

где

u(t) входные параметры
y(t) выходные параметры
x(t) состояния модели с начальным значением x0
$d x (t)$ производный вектор состояния $\dot{x}$ для систем непрерывного времени и вектора обновления состояния $x (t + Δ T)$ для систем дискретного времени. ΔT является шагом расчета.
A(p), B(p), C(p) и D(p) матрицы пространства состояний, параметрированные вектором параметра планирования p.
Параметры p = p(t) измеримые функции входных параметров и состояния модели. Они могут быть скаляром или вектором из нескольких параметров. Набор планирования параметров задает пробел планирования, по которому задана модель LPV.

Блок реализует основанное на сетке представление системы LPV. Вы выбираете сетку значений для параметров планирования. В каждом значении p = p*, вы задаете соответствующую линейную систему как пространство состояний (ss или idss (System Identification Toolbox)) объект модели. Вы используете сгенерированный массив моделей в пространстве состояний, чтобы сконфигурировать блок LPV System.

Блок принимает массив моделей в пространстве состояний с информацией о рабочей точке. Информация о переменных планирования извлечена из SamplingGrid свойство массива LTI. Переменные планирования задают сетку моделей LPV. Они - количества со скалярным знаком, которые могут быть функциями времени, входных параметров и состояний или констант. Они используются, чтобы выбрать локальную динамику на операционном пробеле. Программное обеспечение интерполирует значения этих переменных. Блок использует этот массив с методами интерполяции и экстраполяции данных для симуляции.

Системное представление LPV может быть расширено, чтобы позволить смещениям войти dx, x, u и y переменные. Эта форма известна как affine form модели LPV. Математически, следующее представляет систему LPV:

\begin{array}{l} d x (t) = A (p) x (t) + B (p) u (t) + (\bar{d x} (p) - A (p) \bar{x} (p) - B (p) \bar{u} (p)) \\ y (t) = C (p) x (t) + D (p) u (t) + (\bar{y} (p) - C (p) \bar{x} (p) - D (p) \bar{u} (p)) \\ x (0) = x_{0} \end{array}

(2)

$\bar{d x} (p), \bar{x} (p), \bar{u} (p), \bar{y} (p)$ смещения в значениях dx(t)xt , u(t) и y(t) в данном значении параметров p = p(t).

Чтобы получить такие представления массива линейной системы, линеаризуйте модель Simulink по пакету рабочих точек (см. Пакетную Линеаризацию (Simulink Control Design).) Смещения соответствуют рабочим точкам, в которых вы линеаризовали модель.

Можно получить смещения путем возврата дополнительной информации о линеаризации при вызывании функций такой как linearize (Simulink Control Design) или getIOTransfer (Simulink Control Design). Можно затем извлечь использование смещений getOffsetsForLPV (Simulink Control Design). Для примера см. Приближение LPV Модели Конвертера Повышения (Simulink Control Design).

Нижеследующие ограничения применяются к блоку LPV System:

Внутренние задержки не могут экстраполироваться, чтобы быть меньше их минимального значения в массиве модели в пространстве состояний.
При использовании неправильной сетки линейных моделей, чтобы задать систему LPV, только используется самая близкая соседняя схема интерполяции. Это может уменьшать точность результатов симуляции. Рекомендуется работать с обычными сетками. Чтобы узнать больше об обычных и неправильных сетках, смотрите Регулярный по сравнению с Неправильными Сетками.

Поддержка типов данных

Одни и двойные данные. Необходимо преобразовать любой другой тип данных для входных сигналов или свойств модели к этим типам данных.

Параметры

Диалоговое окно LPV System Block Parameter содержит пять вкладок для определения системных данных, алгоритма планирования и выходных портов. Следующая таблица обобщает параметры блоков.

Задача	Параметры
Задайте массив моделей в пространстве состояний и начальных состояний	Во вкладке LPV Model: State-space array Initial state
Задайте смещения рабочей точки	Во вкладке LPV Model: Input offset Output offset State offset
Задайте смещения в производной состояния или обновите переменную	Во вкладке LPV Model: State derivative/update offset
Задайте, какие матрицы модели фиксируются и их номинальная стоимость, чтобы заменить записи в данных модели. В некоторых ситуациях можно хотеть заменить зависимую параметром матрицу, такую как `A(p)` с фиксированным значением `A` для симуляции. Например, `A` может представлять среднее значение в области значений планирования.	Во вкладке Fixed Entries: Nominal Model Fixed Coefficient Indices
Задайте опции для интерполяции и экстраполяции	Во вкладке Scheduling: Interpolation method Extrapolation method Index search method Begin index search using previous index result
Задайте дополнительные выходные параметры для блока	Во вкладке Outputs: Output states Output state derivatives (continuous-time) or updates (discrete-time) Output interpolated state-space data Output interpolated offsets
Задайте настройки генерации кода	Во вкладке Code Generation: Block data type (discrete-time case only) Initial buffer size for delays Use fixed buffer size

Массив пространства состояний

Массив пространства состояний (ss или idss (System Identification Toolbox)) модели. Все модели в массиве должны использовать то же определение состояний. Используйте SamplingGrid свойство пространства состояний возражает, чтобы задать параметры планирования для модели. Смотрите ss или idss страница модели - ссылки для получения дополнительной информации о SamplingGrid свойство.

Когда блок находится в модели с синхронным государственным контролем (см. блок State Control (HDL Coder)), необходимо задать массив моделей дискретного времени.

Начальное состояние

Начальные условия, чтобы использовать с локальной моделью, чтобы запустить симуляцию, заданное одно из следующего:

0 (Значение по умолчанию)
Двойной вектор из длины равняется количеству состояний модели

Введите смещение

Смещения во входе u(t)В виде одного из следующего:

0 (Значение по умолчанию) — Использование, когда нет никаких входных смещений ( $\bar{u} (p) = 0 \forall p$ ).
Двойной вектор из длины, равной количеству входных параметров — Использование, когда введено возмещенное, является тем же самым через пробел планирования.
Двойной массив размера [nu 1 sysArraySize] — Используют, когда смещения присутствуют, и они варьируются через пробел планирования. Здесь, nu = количество входных параметров, sysArraySize = размер массивов массива пространства состояний. Использование size определить размер массивов.

Можно получить смещения во время линеаризации и преобразовать их в формат, поддержанный блоком LPV System. Для получения дополнительной информации смотрите, что Аппроксимирующее Нелинейное Поведение Использует Массив Систем LTI (Simulink Control Design) и getOffsetsForLPV (Simulink Control Design).

Выведите смещение

Смещения в выходе y(t)В виде одного из следующего:

0 (Значение по умолчанию) — Использование, когда нет никаких выходных смещений $\bar{y} (p) = 0 \forall p$ .
Двойной вектор из длины равняется количеству выходных параметров. Используйте, когда выведенные смещения будут тем же самым через пробел планирования.
Двойной массив размера [ny 1 sysArraySize]. Используйте, когда смещения присутствуют, и они варьируются через пробел планирования. Здесь, ny = количество выходных параметров, sysArraySize = размер массивов массива пространства состояний. Использование size определить размер массивов.

Смещение состояния

Смещения в состояниях x(t)В виде одного из следующего:

0 (Значение по умолчанию) — Использование, когда нет никаких смещений состояния $\bar{x} (p) = 0 \forall p$ .
Двойной вектор из длины равняется количеству состояний. Используйте, когда смещения состояния будут тем же самым через пробел планирования.
Двойной массив размера [nx 1 sysArraySize], где nx = количество состояний, sysArraySize = размер массивов массива пространства состояний. Используйте, когда смещения присутствуют, и они варьируются через пробел планирования. Здесь, nx = количество состояний, sysArraySize = размер массивов массива пространства состояний. Использование size определить размер массивов.

Производная/обновление состояния возмещена

Смещения в производной состояния или переменной dx(t) обновленияВ виде одного из следующего:

Если вы получили массив линейной системы линеаризацией под условиями равновесия, выберите опцию Assume equilibrium conditions. Эта опция соответствует смещению $\bar{d x} (p) = 0$ для системы непрерывного времени и $\bar{d x} (p) = \bar{x} (p)$ для системы дискретного времени. Эта опция выбрана по умолчанию.
Если линейная система содержит по крайней мере одну систему, которую вы получили при неравновесных условиях, очистите опцию Assume equilibrium conditions. Задайте одно из следующего в поле Offset value:
- Если dx возместите значения, то же самое через пробел планирования, задает как двойной вектор из длины, равной количеству состояний.
- Если dx смещения присутствуют, и они варьируются через пробел планирования, задают как двойной массив размера [nx 1 sysArraySize], где nx = количество состояний и sysArraySize = размер массивов массива пространства состояний.

Номинальная модель

Модель в пространстве состояний, которая вводит значения фиксированных коэффициентов в виде одного из следующего:

Use the first model in state-space array (Значение по умолчанию:) — первая модель в массиве пространства состояний используется, чтобы представлять модель LPV. В следующем примере массив пространства состояний задан объектом sys и фиксированные коэффициенты взяты из модели sys(:,:,1).
```
% Specify a 4-by-5 array of state-space models.
sys = rss(4,2,3,4,5);
a = 1:4; 
b = 10:10:50;
[av,bv] = ndgrid(a,b);
% Use "alpha" and "beta" variables as scheduling parameters.
sys.SamplingGrid = struct('alpha',av,'beta',bv);  
```
Фиксированные коэффициенты взяты из модели sysFixed = sys(:,:,1), который соответствует [alpha=1, beta=10]. Если (2,1) запись A матрица обеспечена, чтобы быть зафиксированной, ее значением, используемым во время симуляции, является sysFixed.A(2,1).
Custom value — Задайте различную модель в пространстве состояний для фиксированных записей. Задайте переменную для фиксированной модели в поле State space model. Фиксированная модель должна использовать то же основание состояния в качестве массива пространства состояний в модели LPV.

Фиксированные содействующие индексы

Задайте, какие коэффициенты матриц пространства состояний и векторов задержки фиксируются.

Задайте одно из следующего:

Скалярная булевская переменная (true или false), если все записи матрицы должны быть обработаны тот же путь.
Значением по умолчанию является false для матриц пространства состояний и векторов задержки, что означает, что они обработаны как свободные.

Логическая матрица размера, совместимого с размером соответствующей матрицы:

Матрица пространства состояний	Размер фиксированной матрицы записи
A matrix	`nx`- `nx`
B matrix	`nx`- `nu`
C matrix	`ny`- `nx`
D matrix	`ny`- `nu`
Input delay	`nu`- 1
Output delay	`ny`- 1
Internal delay	`ni`- 1

где, nu = количество входных параметров, ny = количество выходных параметров, nx = количество состояний, ni = длина внутреннего вектора задержки.

Числовые индексы, чтобы задать местоположение фиксированных записей. Смотрите sub2ind страница с описанием для получения дополнительной информации о том, как сгенерировать числовые индексы, соответствующие данному индексу (i,j) для элемента матрицы.

Метод интерполяции

Метод интерполяции. Задает, как данные пространства состояний должны быть вычислены для планирования значений параметров, которые расположены далеко от их местоположений сетки.

Задайте одну из следующих опций:

Flat — Выберите данные пространства состояний в самом близком узле решетки, но не более крупные, чем, текущая точка. Текущая точка является значением параметров планирования в текущее время.
Nearest — Выберите данные пространства состояний в самом близком узле решетки на пробеле планирования.
Linear — Получите данные пространства состояний линейной интерполяцией самых близких 2-х соседей на пробеле планирования, где d = количество планирования параметров.

Схемой интерполяции по умолчанию является Linear для обычных сеток планирования значений параметров. Для неправильных сеток, Nearest схема интерполяции всегда используется независимо от сделанного выбора. чтобы узнать больше об обычных и неправильных сетках, смотрите Регулярный по сравнению с Неправильными Сетками.

Linear метод обеспечивает самую высокую точность, но занимает больше времени, чтобы вычислить. Flat и Nearest методы хороши для моделей, которые имеют динамику переключения режимов.

ExtrapolationMethod

ExtrapolationMethod . Задает, как вычислить данные пространства состояний для планирования значений параметров, которые выходят за пределы области значений, в которой был обеспечен массив пространства состояний (как задано в SamplingGrid свойство.

Задайте одну из следующих опций:

Clip (Значение по умолчанию:) — Отключает экстраполяцию и возвращает данные, соответствующие последнему доступному узлу решетки планирования, который является самым близким к текущей точке.
Linear — Соответствует линии между первой или последней парой значений для каждого параметра планирования, в зависимости от того, меньше ли текущее значение первого или большего, чем последнее значение узла решетки, соответственно. Этот метод возвращает точку на той линии, соответствующей текущему значению. Линейная экстраполяция требует, чтобы схема интерполяции была линейна также.

Метод поиска по индексу

Местоположение текущих значений параметров планирования на пробеле планирования определяется алгоритмом перед поиском. Выберите Linear search или Binary search. Каждый метод поиска имеет преимущества скорости в различных ситуациях. Для получения дополнительной информации об этом параметре смотрите страницу с описанием блока Prelookup (Simulink).

Начните поиск по индексу с помощью предыдущего результата индекса

Установите этот флажок, когда это необходимо, блок, чтобы запустить его поиск с помощью индекса, найденного на предыдущем временном шаге. Для получения дополнительной информации об этом параметре смотрите страницу с описанием блока Prelookup (Simulink).

Состояния вывода

Добавьте x порт с блоком к значениям состояния вывода. Эта опция выбрана по умолчанию.

Производные состояния вывода (непрерывное время) или обновления (дискретное время)

Добавьте dx порт с блоком к значениям производной состояния вывода или обновлению значения. Эта опция выбрана по умолчанию.

Выведите интерполированные данные пространства состояний

Добавьте ss порт с блоком, чтобы вывести данные пространства состояний как структуру. Эта опция выбрана по умолчанию.

Поля сгенерированной структуры:

Матрицы пространства состояний ABCD.
Задержки InputDelay, OutputDelay, и InternalDelay. InternalDelay поле доступно только, когда модель имеет внутреннюю задержку.

Выведите интерполированные смещения

Добавьте offset порт с блоком к смещениям модели выхода LPV $(\bar{u} (p), \bar{y} (p), \bar{x} (p), \bar{d x} (p))$ .

Поля структуры:

InputOffset, OutputOffset, StateOffset, и StateDerivativeOffset в непрерывное время.
InputOffset, OutputOffset, StateOffset, и StateUpdateOffset в дискретное время.

Блокируйте тип данных (только случай дискретного времени)

Поддерживаемый тип данных. Используйте эту опцию только для моделей в пространстве состояний дискретного времени. Задайте double или single.

Размер начального буфера для задержек

Начальное выделение памяти для количества точек ввода, чтобы сохранить для моделей, которые содержат задержки. Если количество точек ввода превышает размер начального буфера, блок выделяет дополнительную память. Размер по умолчанию 1024.

Когда вы запускаете модель в Режиме Accelerator или создаете модель, убедитесь, что размер начального буфера является достаточно большим, чтобы обработать максимальную ожидаемую задержку модели.

Используйте зафиксированный buffer size

Задайте, использовать ли фиксированный buffer size, чтобы избавить задержанные входные и выходные данные от предыдущих временных шагов. Используйте эту опцию в течение непрерывного времени системы LPV, которые содержат задержки ввода или вывода. Если буфер полон, новые данные уже заменяют данные в буфере. Программное обеспечение использует линейную экстраполяцию, чтобы оценить выходные значения, которые не находятся в буфере.

Примеры

Сконфигурируйте параметр планирования Input port

Рассмотрите модель LPV с 4 состояниями, с 3 выходами, с 2 входами. Используйте вход u(2) и x(1) состояния как планирование параметров. Сконфигурируйте модель Simulink как показано в следующем рисунке.

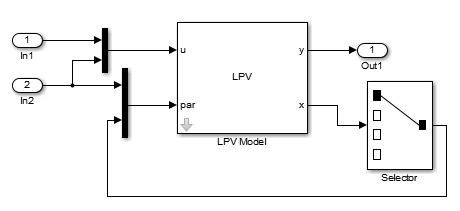
Симулируйте линейную варьирующуюся по параметру систему

Рассмотрите линейную систему массового пружинного демпфера, масса которой изменяется как функция внешней команды загрузки. Управляющее уравнение:

$m (u) \ddot{y} + c \dot{y} + k (y) y = F (t)$

где m(u) масса, зависящая от внешней команды uC коэффициент затухания, k жесткость пружины и F(t) вход принуждения. y(t) положение массы в установленный срок t. Для фиксированного значения u, система линейна и описывается как:

$\begin{array}{l} A = [\begin{matrix} 0 & 1 \\ - \frac{k}{m} & - \frac{c}{m} \end{matrix}], B = [\begin{matrix} 0 \\ \frac{1}{m} \end{matrix}], C = [\begin{matrix} 1 & 0 \end{matrix}] \\ \dot{x} = A x + B u, y = C x \end{array}$

где $x = [\begin{matrix} y \\ \dot{y} \end{matrix}]$ вектор состояния и m значение массы для данного значения u.

В этом примере вы хотите изучить поведение модели в области значений входных значений от 1 до 10 вольт. Для каждого значения u, измерьте массу и вычислите линейное представление системы. Предположим, масса связана с входом отношением: $m (u) = 10 u + 0.1 u^{2}$ . Для значений u в пределах от 1:10 приводит к следующему массиву линейных систем.

% Specify damping coefficient.
c = 5;   
% Specify stiffness.
k = 300; 
% Specify load command.
u = 1:10;
% Specify mass.
m = 10*u + 0.1*u.^2;
% Compute linear system at a given mass value.
for i = 1:length(u)
   A = [0 1; -k/m(i), -c/m(i)];
   B = [0; 1/m(i)];
   C = [1 0];
   sys(:,:,i) = ss(A,B,C,0); 
end

Переменная u вход планирования. Добавьте эту информацию в модель.

sys.SamplingGrid = struct('LoadCommand',u);

Сконфигурируйте блок LPV System:

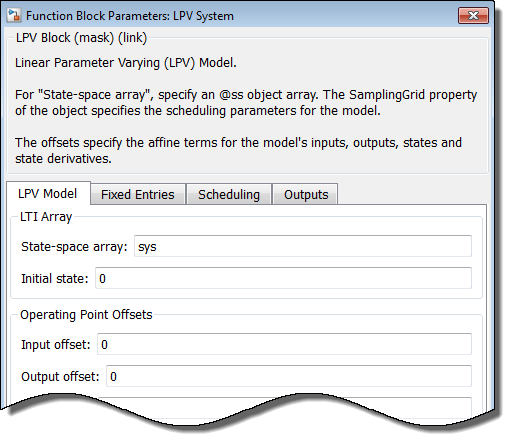
Введите sys в поле State-space array.
Соедините входной порт par к одномерному исходному сигналу, который генерирует значения команды загрузки. Если источник вводит значения между 1 и 10, интерполяция используется для расчета линейная модель в установленный срок экземпляр. В противном случае экстраполяция используется.

Порты

Имя порта	Тип порта (В/)	Описание
u	\in	Входной сигнал u (t) в уравнении 2, описанном ранее. В мультивходном случае этот порт принимает сигнал размерности входа.
паритет	\in	Обеспечивает сигналы для переменных, задающих пробел планирования (“производящий сетку” переменные). Переменные планирования могут быть функциями времени, входных параметров и состояний или констант. Необходимая зависимость может быть достигнута путем подготовки сигнала планирования, использующего вход часов (в течение времени), входной сигнал (`u`), и выходные сигналы (`x`, `dx/dtY`) из блока LPV, как требуется.
y		Выход модели
x		Значения состояний модели
xdot		Значения производных состояния. Производные состояния иногда используются, чтобы задать параметры планирования.
ss		Локальная модель в пространстве состояний на главных шагах времени симуляции
смещение		Смещения модели LPV

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.

Смотрите также

getOffsetsForLPV (Simulink Control Design)

Темы

Введенный в R2014b

Документация

LPV System

Описание

Поддержка типов данных

Параметры

Массив пространства состояний

Начальное состояние

Введите смещение

Выведите смещение

Смещение состояния

Производная/обновление состояния возмещена

Номинальная модель

Фиксированные содействующие индексы

Метод интерполяции

ExtrapolationMethod

Метод поиска по индексу

Начните поиск по индексу с помощью предыдущего результата индекса

Состояния вывода

Производные состояния вывода (непрерывное время) или обновления (дискретное время)

Выведите интерполированные данные пространства состояний

Выведите интерполированные смещения

Блокируйте тип данных (только случай дискретного времени)

Размер начального буфера для задержек

Используйте зафиксированный buffer size

Примеры

Сконфигурируйте параметр планирования Input port

Симулируйте линейную варьирующуюся по параметру систему

Порты

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.

Смотрите также

Темы

Документация Control System Toolbox

Поддержка

Документация

LPV System

Описание

Поддержка типов данных

Параметры

Массив пространства состояний

Начальное состояние

Введите смещение

Выведите смещение

Смещение состояния

Производная/обновление состояния возмещена

Номинальная модель

Фиксированные содействующие индексы

Метод интерполяции

ExtrapolationMethod

Метод поиска по индексу

Начните поиск по индексу с помощью предыдущего результата индекса

Состояния вывода

Производные состояния вывода (непрерывное время) или обновления (дискретное время)

Выведите интерполированные данные пространства состояний

Выведите интерполированные смещения

Блокируйте тип данных (только случай дискретного времени)

Размер начального буфера для задержек

Используйте зафиксированный buffer size

Примеры

Сконфигурируйте параметр планирования Input port

Симулируйте линейную варьирующуюся по параметру систему

Порты

Расширенные возможности

Генерация кода C/C++ Генерация кода C и C++ с помощью Simulink® Coder™.

Смотрите также

Темы

Документация Control System Toolbox

Поддержка

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.