Exponenta Banner

rlocus

График корневого годографа динамической системы

свернуть все на странице

Синтаксис

rlocus(sys)
rlocus(sys1,sys2,...)
[r,k] = rlocus(sys)
r = rlocus(sys,k)

Описание

пример

rlocus(sys) вычисляет и строит корневой годограф модели SISO sys. Корневой годограф возвращает траектории полюса с обратной связью, когда функция обратной связи получает k (принимающий отрицательную обратную связь). Корневые годографы используются, чтобы изучить эффекты изменяния усилений обратной связи на местоположениях полюса с обратной связью. В свою очередь эти местоположения предоставляют косвенную информацию о времени и частотных характеристиках.

Можно использовать rlocus построить схему корневого годографа любого из следующих циклов отрицательной обратной связи установкой sys как показано ниже:

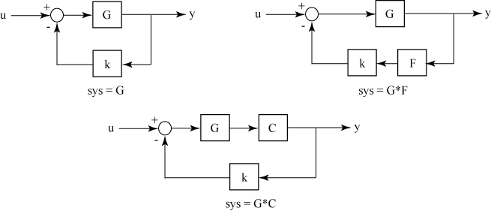
Например, если sys передаточная функция, представленная

sys(s)=n(s)d(s)

полюса с обратной связью являются корнями

d(s)+kn(s)=0

График корневого годографа изображает траектории полюсов с обратной связью когда усиление обратной связи k варьируется от 0 до бесконечности. rlocus адаптивно выбирает набор положительных усилений k произвести сглаженный график. Полюса на графике корневого годографа обозначаются x и нули обозначаются o.

пример

rlocus(sys1,sys2,...) строит корневые годографы нескольких моделей LTI sys1, sys2,... на одном графике. Можно задать цвет, стиль линии и маркер для каждой модели. Еще для большего количества опций настройки графика смотрите rlocusplot.

пример

[r,k] = rlocus(sys) возвращается вектор из обратной связи получает k и комплексные корневые местоположения r для этих усилений.

пример

r = rlocus(sys,k) использует заданный пользователями вектор из усилений обратной связи k выводить полюса с обратной связью r это задает график корневого годографа.

Примеры

свернуть все

Скрипт Open Live Script

Для этого примера. постройте корневой годограф следующей динамической системы SISO:

sys(s)=2s2+5s+1s2+2s+3.

sys = tf([2 5 1],[1 2 3]);
rlocus(sys)

Полюса системы обозначаются x, в то время как нули обозначаются o на графике корневого годографа. Можно использовать меню в рамках сгенерированного графика корневого годографа добавить линии сетки, увеличение или, и также вызвать Property Editor, чтобы настроить график.

Для большего количества опций настройки графика используйте rlocusplot.

Скрипт Open Live Script

В данном примере рассмотрите sisoModels.mat который содержит следующие три модели SISO:

  • sys1 - модель передаточной функции

  • sys2 - модель в пространстве состояний

  • sys3 - модель нулей, полюсов и усиления

Загрузите модели от mat файл. 

load('sisoModels.mat','sys1','sys2','sys3');

Создайте график корневого годографа с помощью rlocus и задайте цвет для каждой системы. Также добавьте легенду в график корневого годографа.

rlocus(sys1,'b',sys2,'k',sys3,'r')
hold on
legend('sys1','sys2','sys3')
hold off

Фигура содержит схемы корневого годографа для всех трех систем в том же графике. Для большего количества индивидуальной настройки графика смотрите rlocusplot.

Скрипт Open Live Script

В данном примере рассмотрите следующую модель передаточной функции SISO:

sys(s)=3s2+19s3+7s2+5s+6

Используйте вышеупомянутую модель передаточной функции с rlocus чтобы извлечь полюса с обратной связью и сопоставленную обратную связь получают значения.

sys = tf([3 1],[9 7 5 6]);
[r,k] = rlocus(sys)
r = 3×53 complex

  -0.9406 + 0.0000i  -0.8744 + 0.0000i  -0.8685 + 0.0000i  -0.8620 + 0.0000i  -0.8550 + 0.0000i  -0.8475 + 0.0000i  -0.8394 + 0.0000i  -0.8306 + 0.0000i  -0.8212 + 0.0000i  -0.8111 + 0.0000i  -0.8003 + 0.0000i  -0.7888 + 0.0000i  -0.7766 + 0.0000i  -0.7636 + 0.0000i  -0.7500 + 0.0000i  -0.7358 + 0.0000i  -0.7209 + 0.0000i  -0.7055 + 0.0000i  -0.6896 + 0.0000i  -0.6734 + 0.0000i  -0.6569 + 0.0000i  -0.6402 + 0.0000i  -0.6236 + 0.0000i  -0.6071 + 0.0000i  -0.5908 + 0.0000i  -0.5748 + 0.0000i  -0.5593 + 0.0000i  -0.5443 + 0.0000i  -0.5299 + 0.0000i  -0.5161 + 0.0000i  -0.5030 + 0.0000i  -0.4906 + 0.0000i  -0.4789 + 0.0000i  -0.4679 + 0.0000i  -0.4576 + 0.0000i  -0.4480 + 0.0000i  -0.4390 + 0.0000i  -0.4306 + 0.0000i  -0.4229 + 0.0000i  -0.4157 + 0.0000i  -0.4090 + 0.0000i  -0.4029 + 0.0000i  -0.3972 + 0.0000i  -0.3919 + 0.0000i  -0.3871 + 0.0000i  -0.3826 + 0.0000i  -0.3785 + 0.0000i  -0.3748 + 0.0000i  -0.3713 + 0.0000i  -0.3681 + 0.0000i
   0.0814 + 0.8379i   0.0483 + 0.9140i   0.0453 + 0.9212i   0.0421 + 0.9291i   0.0386 + 0.9377i   0.0349 + 0.9470i   0.0308 + 0.9573i   0.0264 + 0.9686i   0.0217 + 0.9809i   0.0167 + 0.9943i   0.0113 + 1.0090i   0.0055 + 1.0251i  -0.0006 + 1.0426i  -0.0071 + 1.0617i  -0.0139 + 1.0826i  -0.0210 + 1.1053i  -0.0284 + 1.1300i  -0.0362 + 1.1568i  -0.0441 + 1.1859i  -0.0522 + 1.2175i  -0.0605 + 1.2515i  -0.0688 + 1.2883i  -0.0771 + 1.3278i  -0.0853 + 1.3703i  -0.0935 + 1.4158i  -0.1015 + 1.4644i  -0.1092 + 1.5162i  -0.1167 + 1.5714i  -0.1239 + 1.6299i  -0.1308 + 1.6920i  -0.1374 + 1.7578i  -0.1436 + 1.8273i  -0.1494 + 1.9006i  -0.1549 + 1.9780i  -0.1601 + 2.0594i  -0.1649 + 2.1452i  -0.1694 + 2.2354i  -0.1736 + 2.3302i  -0.1775 + 2.4299i  -0.1810 + 2.5345i  -0.1844 + 2.6442i  -0.1875 + 2.7594i  -0.1903 + 2.8802i  -0.1929 + 3.0069i  -0.1953 + 3.1397i  -0.1976 + 3.2789i  -0.1996 + 3.4247i  -0.2015 + 3.5775i  -0.2032 + 3.7375i  -0.2048 + 3.9052i
   0.0814 - 0.8379i   0.0483 - 0.9140i   0.0453 - 0.9212i   0.0421 - 0.9291i   0.0386 - 0.9377i   0.0349 - 0.9470i   0.0308 - 0.9573i   0.0264 - 0.9686i   0.0217 - 0.9809i   0.0167 - 0.9943i   0.0113 - 1.0090i   0.0055 - 1.0251i  -0.0006 - 1.0426i  -0.0071 - 1.0617i  -0.0139 - 1.0826i  -0.0210 - 1.1053i  -0.0284 - 1.1300i  -0.0362 - 1.1568i  -0.0441 - 1.1859i  -0.0522 - 1.2175i  -0.0605 - 1.2515i  -0.0688 - 1.2883i  -0.0771 - 1.3278i  -0.0853 - 1.3703i  -0.0935 - 1.4158i  -0.1015 - 1.4644i  -0.1092 - 1.5162i  -0.1167 - 1.5714i  -0.1239 - 1.6299i  -0.1308 - 1.6920i  -0.1374 - 1.7578i  -0.1436 - 1.8273i  -0.1494 - 1.9006i  -0.1549 - 1.9780i  -0.1601 - 2.0594i  -0.1649 - 2.1452i  -0.1694 - 2.2354i  -0.1736 - 2.3302i  -0.1775 - 2.4299i  -0.1810 - 2.5345i  -0.1844 - 2.6442i  -0.1875 - 2.7594i  -0.1903 - 2.8802i  -0.1929 - 3.0069i  -0.1953 - 3.1397i  -0.1976 - 3.2789i  -0.1996 - 3.4247i  -0.2015 - 3.5775i  -0.2032 - 3.7375i  -0.2048 - 3.9052i


k = 1×53
104 ×

         0    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0002    0.0002    0.0002    0.0002    0.0002    0.0003    0.0003    0.0003    0.0003    0.0004    0.0004    0.0004    0.0005    0.0005    0.0006    0.0006    0.0007    0.0007    0.0008    0.0009    0.0010    0.0011    0.0012    0.0013    0.0014    0.0015    0.0017    0.0018    0.0020    0.0022    0.0024    0.0026    0.0028    0.0031    0.0034    0.0037    0.0041    0.0045

Начиная с sys содержит 3 полюса, размер результирующего массива полюсов r 3x53. Каждый столбец в r соответствует значению усиления от векторного k. В данном примере rlocus автоматически выбрал 53 значения k от нуля до бесконечности, чтобы получить сглаженную траекторию для трех полюсов с обратной связью. 

display(r(:,39))
  -0.4229 + 0.0000i
  -0.1775 + 2.4299i
  -0.1775 - 2.4299i

display(k(39))
   16.5907

Например, r(:,39) содержит вышеупомянутые полюса с обратной связью для значения усиления обратной связи 16,5907.

Скрипт Open Live Script

В данном примере рассмотрите следующую модель передаточной функции SISO:

sys(s)=0.5s2-14s4+3s2+2

Задайте модель передаточной функции и требуемый вектор из значений усиления обратной связи. В данном примере рассмотрите набор значений усиления, варьирующихся от 1 до 8 с шагом 0,5, и извлеките местоположения полюса с обратной связью с помощью rlocus.

sys = tf([0.5 -1],[4 0 3 0 2]);
k = (1:0.5:5);
r = rlocus(sys,k);
size(r)
ans = 1×2

     4     9

Начиная с sys содержит 4 полюса с обратной связью, размер результирующего массива закрытых полюсных местоположений r 4x9, где эти 9 столбцов соответствуют 9 определенным значениям усиления, заданным в k.

Можно также визуализировать траекторию полюсов с обратной связью для определенных значений усиления в k на графике корневого годографа. 

rlocus(sys,k)

Входные параметры

свернуть все

Динамическая система SISO в виде одного из следующего:

  • Числовые модели LTI непрерывного времени или дискретного времени, которые включают tf, zpk, или ss модели.

  • Обобщенные или неопределенные модели LTI такой как genss или uss Модели (Robust Control Toolbox). (Используя неопределенные модели требует программного обеспечения Robust Control Toolbox™.)

    rlocus принимает

    • текущие значения настраиваемых компонентов для настраиваемых блоков системы управления.

    • номинальные значения модели для неопределенных блоков системы управления.

  • Идентифицированные модели LTI, такой как idtf (System Identification Toolbox), idss (System Identification Toolbox), idproc (System Identification Toolbox), idpoly (System Identification Toolbox), и idgrey Модели (System Identification Toolbox). (Используя идентифицированные модели требует программного обеспечения System Identification Toolbox™.)

Значения усиления обратной связи, которые принадлежат местоположениям полюса в виде вектора. Усиления обратной связи задают траекторию полюсов, таким образом, влияющих на форму графика корневого годографа.

Выходные аргументы

свернуть все

Местоположения полюса с обратной связью sys соответствие каждому значению в k, возвращенный как n- m массив, где n количество полюсов с обратной связью sys и m = max(length(k)).

Значения усиления обратной связи, которые принадлежат местоположениям полюса, возвратились как вектор. Усиления обратной связи задают траекторию полюсов, таким образом, влияющих на форму графика корневого годографа. Когда k не задан пользователем, rlocus адаптивно выбирает набор положительных усилений k между нулем и бесконечностью, чтобы произвести сглаженный график.

Советы

  • Для интерактивного подхода к графическому выводу корневого годографа смотрите Control System Designer.

Смотрите также

| | | | | |

Темы

Представлено до R2006a

Документация Control System Toolbox

Поддержка