Сравните прогнозирующую эффективность после создания моделей Используя приложение Econometric Modeler

В этом примере показано, как выбрать задержки для модели ARIMA путем сравнения значений AIC предполагаемых моделей с помощью приложения Econometric Modeler. Пример также показывает, как сравнить прогнозирующую эффективность нескольких моделей, у которых случаются лучшие судороги в выборке в командной строке. Набор данных Data_Airline.mat содержит ежемесячные количества авиапассажиров.

Импортируйте данные в Econometric Modeler

В командной строке загрузите Data_Airline.mat набор данных.

load Data_Airline

Чтобы сравнить прогнозирующую эффективность позже, зарезервируйте прошлые два года данных как выборка затяжки.

fHorizon = 24;
HoldoutTable = DataTable((end - fHorizon + 1):end,:);
DataTable((end - fHorizon + 1):end,:) = [];

В командной строке откройте приложение Econometric Modeler.

econometricModeler

В качестве альтернативы откройте приложение из галереи Apps (см. Econometric Modeler).

Импортируйте DataTable в приложение:

На вкладке Econometric Modeler, в разделе Import, нажатии кнопки.
В диалоговом окне Import Data, в столбце Import?, устанавливают флажок для DataTable переменная.
Нажмите Import.

Переменная PSSG появляется в Data Browser, и его график временных рядов появляется в окне рисунка Time Series Plot(PSSG).

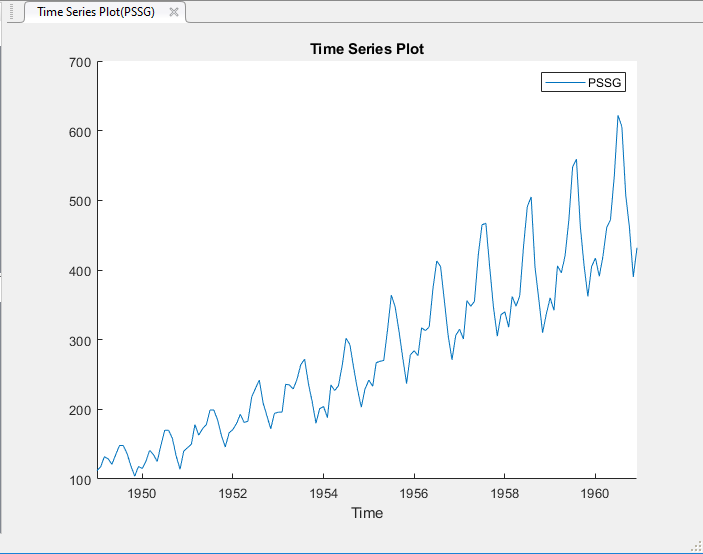
Ряд показывает сезонный тренд, последовательную корреляцию и возможный экспоненциальный рост. Для интерактивного анализа последовательной корреляции смотрите, Обнаруживают Последовательную Корреляцию Используя Приложение Econometric Modeler.

Удалите экспоненциальный тренд

Обратитесь к экспоненциальному тренду путем применяния логарифмического преобразования к PSSG.

В Data Browser выберите PSSG.
На вкладке Econometric Modeler, в разделе Transforms, нажимают Log.

Преобразованная переменная PSSGLog появляется в Data Browser, и его график временных рядов появляется в окне рисунка Time Series Plot(PSSGLog).

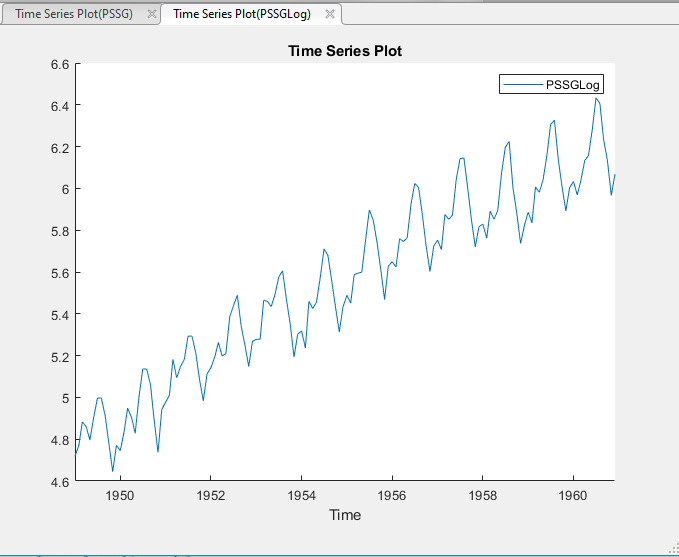
Экспоненциальный рост, кажется, удален из ряда.

Сравните подгонки в демонстрационной модели

Поле, Дженкинс и Рейнсель предлагают SARIMA (0,1,1) × (0,1,1) ₁₂ моделей без константы для PSSGLog [1] (для получения дополнительной информации смотрите Оценку Мультипликативная Модель ARIMA Используя Приложение Econometric Modeler). Однако рассмотрите все комбинации ежемесячных моделей SARIMA, которые включают до двух сезонных и несезонных задержек MA. А именно, выполните итерации следующих шагов для каждой из девяти моделей формы SARIMA (0,1, q) × (0,1, q ₁₂) ₁₂, где q ∈ {0,1,2} и q ₁₂ ∈ {0,1,2}.

Для первой итерации:
1. Позвольте q = q ₁₂ = 0.
2. С PSSGLog выбранный в Data Browser, кликните по вкладке Econometric Modeler. В разделе Models кликните по стреле, чтобы отобразить галерею моделей.
3. В галерее моделей, в разделе ARMA/ARIMA Models, нажимают SARIMA.
4. В диалоговом окне SARIMA Model Parameters, на вкладке Lag Order:
  - Раздел Nonseasonal
    Установите Degrees of Integration на 1.
    Установите Moving Average Order на 0.
    Снимите флажок Include Constant Term.
  - Раздел Seasonal
    Установите Period на 12 указать на ежемесячные данные.
    Установите Moving Average Order на 0.
    Установите флажок Include Seasonal Difference.
5. Нажмите Estimate.
Переименуйте новую переменную модели.
1. В Data Browser щелкните правой кнопкой по новой переменной модели.
2. В контекстном меню выберите Rename.
3. Введите SARIMA01qx01_q12. Например, когда q = _q12 = 0, переименуйте переменную в SARIMA010x010.
В сводных данных модели (SARIMA01qx01_q12) документ, в таблице Goodness of Fit, отмечает значение AIC. Например, для переменной SARIMA010x010 модели, AIC находится в этом рисунке.
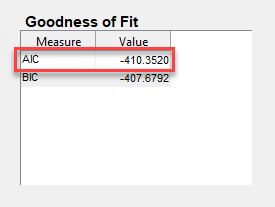
Для следующей итерации, выбрал значения q и q ₁₂. Например, q = 0 и q ₁₂ = 1 для второй итерации.
В Data Browser щелкните правой кнопкой по SARIMA01qx01_q12. В контекстном меню выберите Modify, чтобы открыть диалоговое окно SARIMA Model Parameters с текущими настройками для выбранной модели.
В диалоговом окне SARIMA Model Parameters:
1. В разделе Nonseasonal, набор Moving Average Order к q.
2. В разделе Seasonal, набор Moving Average Order к _q12.
3. Нажмите Estimate.

После того, как вы завершите шаги, раздел Models Data Browser содержит девять предполагаемых моделей под названием SARIMA010x010 через SARIMA012x012.

Получившиеся значения AIC находятся в этой таблице.

Модель	Имя переменной	AIC
SARIMA (0,1,0) × (0,1,0) ₁₂	`SARIMA010x010`	-410.3520
SARIMA (0,1,0) × (0,1,1) ₁₂	`SARIMA010x011`	-443.0009
SARIMA (0,1,0) × (0,1,2) ₁₂	`SARIMA010x012`	-441.0010
SARIMA (0,1,1) × (0,1,0) ₁₂	`SARIMA011x010`	-422.8680
SARIMA (0,1,1) × (0,1,1) ₁₂	`SARIMA011x011`	-452.0039
SARIMA (0,1,1) × (0,1,2) ₁₂	`SARIMA011x012`	-450.0605
SARIMA (0,1,2) × (0,1,0) ₁₂	`SARIMA012x010`	-420.9760
SARIMA (0,1,2) × (0,1,1) ₁₂	`SARIMA012x011`	-450.0087
SARIMA (0,1,2) × (0,1,2) ₁₂	`SARIMA012x012`	-448.0650

Эти три модели, дающие к самым низким трем значениям AIC, являются SARIMA (0,1,1) × (0,1,1) ₁₂, SARIMA (0,1,1) × (0,1,2) ₁₂ и SARIMA (0,1,2) × (0,1,1) ₁₂. Эти модели имеют лучшую экономную подгонку в выборке.

Экспорт лучшие модели к рабочей области

Экспортируйте модели с лучшими подгонками в выборке.

На вкладке Econometric Modeler, в разделе Export, нажатии кнопки.
В диалоговом окне Export Variables, в столбце Models, кликают по флажку Select для SARIMA011x011, SARIMA011x012, и SARIMA012x011. Снимите флажок для любых других выбранных моделей.
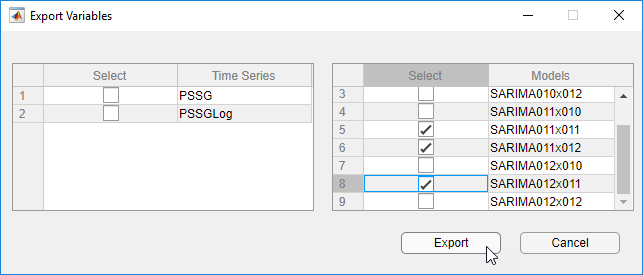
Нажмите Export.

arima объекты модели SARIMA011x011, SARIMA011x012, и SARIMA012x011 появитесь в MATLAB^® Workspace.

Оцените прогнозы

В командной строке оцените прогнозы "два года вперед" для каждой модели.

f5 = forecast(SARIMA_PSSGLog5,fHorizon);
f6 = forecast(SARIMA_PSSGLog6,fHorizon);
f8 = forecast(SARIMA_PSSGLog8,fHorizon);

f5, f6, и f8 24 1 векторы, содержащие прогнозы.

Сравните среднеквадратичные погрешности предсказания

Оцените среднеквадратичную погрешность предсказания (PMSE) для каждого из векторов прогноза.

logPSSGHO = log(HoldoutTable.Variables);
pmse5 = mean((logPSSGHO - f5).^2);
pmse6 = mean((logPSSGHO - f6).^2);
pmse8 = mean((logPSSGHO - f8).^2);

Идентифицируйте модель, дающую к самому низкому PMSE.

[~,bestIdx] = min([pmse5 pmse6 pmse8],[],2)

SARIMA (0,1,1) × (0,1,1) ₁₂ моделей выполняет лучший в выборке и из выборки.

Ссылки

[1] Поле, Джордж Э. П., Гвилим М. Дженкинс и Грегори К. Рейнсель. Анализ Временных Рядов: Прогнозирование и Управление. 3-й редактор Englewood Cliffs, NJ: Prentice Hall, 1994.

Документация