Exponenta Banner
exponenta event banner

graphallshortestpaths

Найдите все кратчайшие пути в графике

Синтаксис

[dist] = graphallshortestpaths(G)
[dist] = graphallshortestpaths(G, ...'Directed', DirectedValue, ...)
[dist] = graphallshortestpaths(G, ...'Weights', WeightsValue, ...)

Аргументы

G N на n разреженная матрица, которая представляет график. Ненулевые записи в матричном G представляйте веса ребер.
DirectedValueСвойство, которое указывает, направлен ли график или неориентированный. Введите false для неориентированного графа. Это приводит к верхнему треугольнику проигнорированной разреженной матрицы. Значением по умолчанию является true.
WeightsValueВектор-столбец, который задает пользовательские веса для ребер в матричном G. Это должно иметь одну запись для каждого ненулевого значения (ребро) в матричном G. Порядок пользовательских весов в векторе должен совпадать с порядком ненулевых значений в матричном G когда это пересечено по столбцам. Это свойство позволяет вам использовать веса с нулевым знаком. По умолчанию, graphallshortestpaths получает информацию веса от ненулевых записей в матричном G.

Описание

Совет

Дополнительные сведения о функциях теории графов см. в Функциях Теории графов.

[dist] = graphallshortestpaths(G) находит кратчайшие пути между каждой парой узлов в графике представленными матричным G, использование алгоритма Джонсона. Введите G N на n разреженная матрица, которая представляет график. Ненулевые записи в матричном G представляйте веса ребер.

Выведите dist N на n матрица где dists, t расстояние кратчайшего пути от исходного узла S предназначаться для узла T. Элементами в диагонали этой матрицы всегда является 0, указание на исходный узел и целевой узел является тем же самым. 0 не в диагонали указывает, что расстоянием между исходным узлом и целевым узлом является 0. Inf указывает, что нет никакого пути между исходным узлом и целевым узлом.

Алгоритм Джонсона имеет временную сложность O(N*log(N)+N*E), где N и E количество узлов и ребер соответственно.

[...] = graphallshortestpaths (GPropertyName ', PropertyValue, ...) вызовы graphallshortestpaths с дополнительными свойствами, которые используют имя свойства / пары значения свойства. Можно задать одно или несколько свойств в любом порядке. Каждый PropertyName должен быть заключен в одинарные кавычки и нечувствительный к регистру. Это имя свойства / пары значения свойства следующие:

[dist] = graphallshortestpaths(G, ...'Directed', DirectedValue, ...) указывает, направлен ли график или неориентированный. Установите DirectedValue к false для неориентированного графа. Это приводит к верхнему треугольнику проигнорированной разреженной матрицы. Значением по умолчанию является true.

[dist] = graphallshortestpaths(G, ...'Weights', WeightsValue, ...) позволяет вам задать пользовательские веса для ребер. WeightsValue вектор-столбец, имеющий одну запись для каждого ненулевого значения (ребро) в матричном G. Порядок пользовательских весов в векторе должен совпадать с порядком ненулевых значений в матричном G когда это пересечено по столбцам. Это свойство позволяет вам использовать веса с нулевым знаком. По умолчанию, graphallshortestpaths получает информацию веса от ненулевых записей в матричном G.

Примеры

Пример 31. Нахождение всех кратчайших путей в ориентированном графе

  1. Создайте и просмотрите ориентированного графа с 6 узлами и 11 ребрами.

    W = [.41 .99 .51 .32 .15 .45 .38 .32 .36 .29 .21];
DG = sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],W)

DG =

   (4,1)       0.4500
   (6,2)       0.4100
   (2,3)       0.5100
   (5,3)       0.3200
   (6,3)       0.2900
   (3,4)       0.1500
   (5,4)       0.3600
   (1,5)       0.2100
   (2,5)       0.3200
   (1,6)       0.9900
   (4,6)       0.3800

view(biograph(DG,[],'ShowWeights','on'))

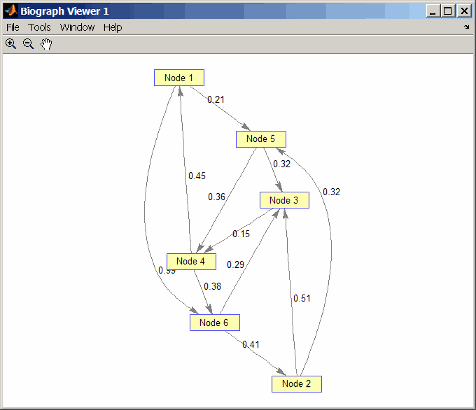
  2. Найдите все кратчайшие пути между каждой парой узлов в ориентированном графе.

    graphallshortestpaths(DG)

ans =

         0    1.3600    0.5300    0.5700    0.2100    0.9500
    1.1100         0    0.5100    0.6600    0.3200    1.0400
    0.6000    0.9400         0    0.1500    0.8100    0.5300
    0.4500    0.7900    0.6700         0    0.6600    0.3800
    0.8100    1.1500    0.3200    0.3600         0    0.7400
    0.8900    0.4100    0.2900    0.4400    0.7300         0

    Получившаяся матрица показывает, что кратчайший путь от узла 1 (первая строка) к узлу 6 (шестой столбец) 0.95. Вы видите это в графике путем трассировки пути от узла 1 к узлу 5 к узлу 4 к узлу 6 (0.21 + 0.36 + 0.38 = 0.95).

Пример 32. Нахождение всех кратчайших путей в неориентированном графе

  1. Создайте и просмотрите неориентированного графа с 6 узлами и 11 ребрами.

    UG = tril(DG + DG')

UG =

   (4,1)       0.4500
   (5,1)       0.2100
   (6,1)       0.9900
   (3,2)       0.5100
   (5,2)       0.3200
   (6,2)       0.4100
   (4,3)       0.1500
   (5,3)       0.3200
   (6,3)       0.2900
   (5,4)       0.3600
   (6,4)       0.3800

view(biograph(UG,[],'ShowArrows','off','ShowWeights','on'))

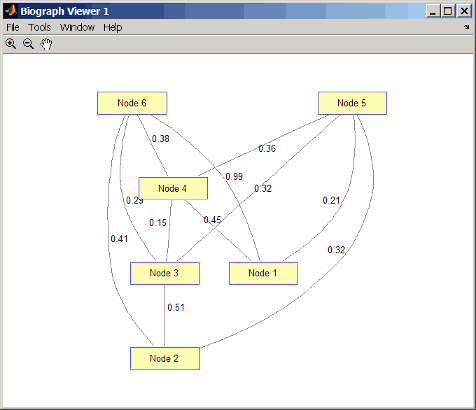
  2. Найдите все кратчайшие пути между каждой парой узлов в неориентированном графе.

    graphallshortestpaths(UG,'directed',false)

ans =

         0    0.5300    0.5300    0.4500    0.2100    0.8300
    0.5300         0    0.5100    0.6600    0.3200    0.7000
    0.5300    0.5100         0    0.1500    0.3200    0.5300
    0.4500    0.6600    0.1500         0    0.3600    0.3800
    0.2100    0.3200    0.3200    0.3600         0    0.7400
    0.8300    0.7000    0.5300    0.3800    0.7400         0

    Получившаяся матрица симметрична, потому что она представляет неориентированного графа. Это показывает, что кратчайший путь от узла 1 (первая строка) к узлу 6 (шестой столбец) 0.83. Вы видите это в графике путем трассировки пути от узла 1 к узлу 4 к узлу 6 (0.45 + 0. 38 = 0.83). Поскольку UG неориентированный граф, мы можем использовать ребро между узлом 1 и узлом 4, который мы не могли сделать в ориентированном графе DG.

Ссылки

[1] Джонсон, D.B. (1977). Эффективные алгоритмы для кратчайших путей в разреженных сетях. Журнал ACM 24 (1), 1-13.

[2] Siek, J.G., Ли, L-Q и Lumsdaine, A. (2002). Руководство пользователя библиотеки графика повышения и справочник, (верхний Сэддл-Ривер, образование НДЖ:ПИРСОНА).

Смотрите также

| | | | | | | | | |

Представленный в R2006b

Документация Bioinformatics Toolbox

Поддержка