graphconncomp

Найдите строго или слабо соединенные компоненты в графике

Синтаксис

[S, C] = graphconncomp(G) [S, C] = graphconncomp(G, ...'Directed', DirectedValue, ...) [S, C] = graphconncomp(G, ...'Weak', WeakValue, ...)

Аргументы

`G`	N на n разреженная матрица, которая представляет график. Ненулевые записи в матричном `G` укажите на присутствие ребра.
`DirectedValue`	Свойство, которое указывает, направлен ли график или неориентированный. Введите `false` для неориентированного графа. Это приводит к верхнему треугольнику проигнорированной разреженной матрицы. Значением по умолчанию является `true`. Основанный на DFS алгоритм вычисляет связанные компоненты. Временной сложностью является `O(N+E)`, где `N` и `E` количество узлов и ребер соответственно.
`WeakValue`	Свойство, которое указывает, найти ли слабо соединенные компоненты или строго соединенные компоненты. Слабо связанный компонент является максимальной группой узлов, которые взаимно достижимы путем нарушения направлений ребра. Установите `WeakValue` к `true` найти слабо соединенные компоненты. Значением по умолчанию является `false`, который находит строго соединенные компоненты. Состояние этого параметра не оказывает влияния на неориентированных графов, потому что слабо и строго связанные компоненты то же самое в неориентированных графах. Временной сложностью является `O(N+E)`, где `N` и `E` количество узлов и ребер соответственно.

Описание

Совет

Дополнительные сведения о функциях теории графов см. в Функциях Теории графов.

[S, C] = graphconncomp(G) находит строго связанные компоненты графика представленными матричным G использование алгоритма Тарьяна. Строго связанный компонент является максимальной группой узлов, которые взаимно достижимы, не нарушая направления ребра. Введите G N на n разреженная матрица, которая представляет график. Ненулевые записи в матричном G укажите на присутствие ребра.

Количество найденных компонентов возвращено в S, и C указание вектора, которому компоненту принадлежит каждый узел.

Алгоритм Тарьяна имеет временную сложность O(N+E), где N и E количество узлов и ребер соответственно.

SC] = graphconncomp (GPropertyName ', PropertyValue, ...) вызовы graphconncomp с дополнительными свойствами, которые используют имя свойства / пары значения свойства. Можно задать одно или несколько свойств в любом порядке. Каждый PropertyName должен быть заключен в одинарные кавычки и нечувствительный к регистру. Это имя свойства / пары значения свойства следующие:

[S, C] = graphconncomp(G, ...'Directed', DirectedValue, ...) указывает, направлен ли график или неориентированный. Установите directedValue к false для неориентированного графа. Это приводит к верхнему треугольнику проигнорированной разреженной матрицы. Значением по умолчанию является true. Основанный на DFS алгоритм вычисляет связанные компоненты. Временной сложностью является O(N+E), где N и E количество узлов и ребер соответственно.

[S, C] = graphconncomp(G, ...'Weak', WeakValue, ...) указывает, найти ли слабо соединенные компоненты или строго соединенные компоненты. Слабо связанный компонент является максимальной группой узлов, которые взаимно достижимы путем нарушения направлений ребра. Установите WeakValue к true найти слабо соединенные компоненты. Значением по умолчанию является false, который находит строго соединенные компоненты. Состояние этого параметра не оказывает влияния на неориентированных графов, потому что слабо и строго связанные компоненты то же самое в неориентированных графах. Временной сложностью является O(N+E), где N и E количество узлов и ребер соответственно.

Примечание

По определению один узел может быть строго связанным компонентом.

Примечание

Направленный граф без петель (DAG) не может иметь никаких строго связанных компонентов, больше, чем один.

Примеры

Создайте и просмотрите ориентированного графа с 10 узлами и 17 ребрами.

DG = sparse([1 1 1 2 2 3 3 4 5 6 7 7 8 9 9  9 9], ...
           [2 6 8 3 1 4 2 5 4 7 6 4 9 8 10 5 3],true,10,10)

DG =

   (2,1)        1
   (1,2)        1
   (3,2)        1
   (2,3)        1
   (9,3)        1
   (3,4)        1
   (5,4)        1
   (7,4)        1
   (4,5)        1
   (9,5)        1
   (1,6)        1
   (7,6)        1
   (6,7)        1
   (1,8)        1
   (9,8)        1
   (8,9)        1
   (9,10)       1

h = view(biograph(DG));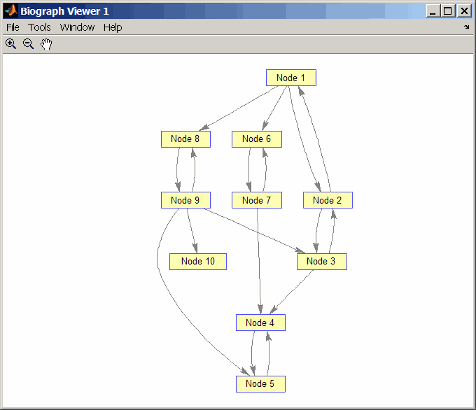

Найдите количество строго связанных компонентов в ориентированном графе и определите, которому компоненту принадлежит каждый из этих 10 узлов.
```
[S,C] = graphconncomp(DG)

S =

     4


C =

     4     4     4     1     1     2     2     4     4     3
```
Окрасьте узлы для каждого компонента с различным цветом.
```
colors = jet(S);
for i = 1:numel(h.nodes)
  h.Nodes(i).Color = colors(C(i),:);
end
```

Ссылки

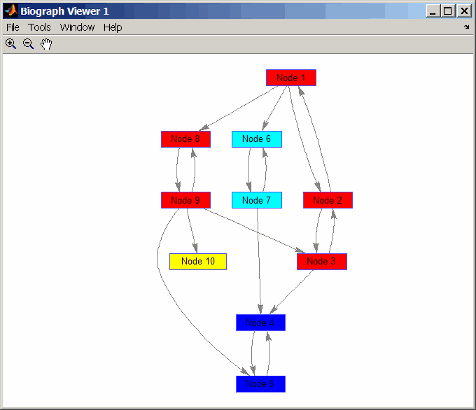
[1] Тарьян, R.E., (1972). Поиск в глубину и линейные алгоритмы графика. SIAM Journal при Вычислении 1 (2), 146–160.

[2] Sedgewick, R., (2002). Алгоритмы на C++, алгоритмы графика части 5 (Аддисон-Уэсли).

[3] Siek, J.G., Ли, L-Q и Lumsdaine, A. (2002). Руководство пользователя библиотеки графика повышения и справочник, (верхний Сэддл-Ривер, образование НДЖ:ПИРСОНА).

Документация

graphconncomp

Синтаксис

Аргументы

Описание

Примеры

Ссылки

Смотрите также

Документация Bioinformatics Toolbox

Поддержка