Синхронный двигатель с постоянными магнитами, заданный в терминах потокосцепления
Simscape / Электрический / Электромеханический / Постоянный магнит
Блок FEM-Parameterized PMSM реализует модель постоянного магнита синхронного двигателя (PMSM), заданного в терминах магнитного потокосцепления. Вы параметрируете блок путем введения таблицы данных моторного магнитного потока в зависимости от угла ротора и текущего. Это - способ, которым сторонние магнитные пакеты метода конечных элементов (FEM) обычно экспортируют информацию о потоке. Из-за табличной формы поток может варьироваться нелинейным способом и на углу ротора и на текущий. Можно поэтому использовать этот блок для модели PMSM с трапециевидным профилем коэффициента противо-ЭДС, иногда названным бесщеточным двигателем постоянного тока, а также регулярным PMSM.
Рисунок показывает эквивалентную схему для соединенного звездой PMSM. Угол ротора является нулем, когда поток постоянного магнита выравнивает с A-фазой магнитную ось.
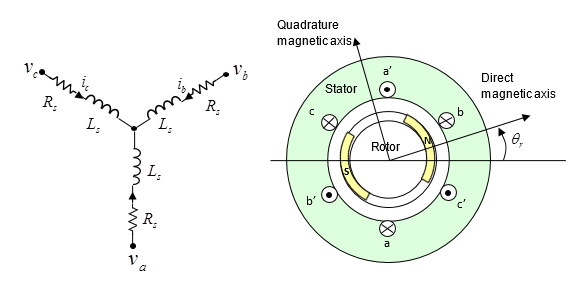
На практике поток, соединяющий каждую из этих трех обмоток, зависит от всех трех токов и угла ротора. Сведение в таблицу потока в зависимости от четырех независимых переменных может привести к неэффективности симуляции и значительным требованиям к памяти, чтобы управлять данными. Блок, поэтому, позволяет вам выбрать между следующими методами параметризации для потока и крутящего момента:
2-D partial derivative data — 2D поиск по таблице, с опциями, чтобы свести в таблицу в терминах текущего и угла ротора, или в терминах d- ось и q- токи оси. Право преимущественной покупки принимает постоянную взаимную индуктивность и поддерживает несинусоидальные профили коэффициента противо-ЭДС. Вторая опция принимает синусоидальный коэффициент противо-ЭДС и получает эффекты насыщения для внутренней части PMSMs (IPMSMs).
3-D partial derivative data — 3-D поиск по таблице, на основе постоянного тока, текущая квадратура, и угол ротора. Вы обеспечиваете данные о поиске потока для фазы a. Парк использования блока преобразовывает, чтобы сопоставить три статора извилистые токи с квадратурные токи и прямому. Этот метод уменьшает сложность данных, по сравнению с 4-D поиском по таблице, и поэтому приводит к улучшаемой производительности симуляции.
4-D partial derivative data — Поиск по таблице 4-D, на основе трех статоров извилистые токи и угол ротора. Вы обеспечиваете данные о поиске потока для фазы a. Эта модель имеет лучшую точность этих трех, но также и является самой дорогостоящей в терминах эффективности симуляции и требований к памяти.
3-D flux linkage data — 3-D поиск по таблице, на основе данных о потокосцеплении. Можно обеспечить данные о потокосцеплении во множестве форматов. Парк использования блока преобразовывает, чтобы сопоставить три статора извилистые токи с квадратурные токи и прямому. Этот метод уменьшает сложность данных, по сравнению с 4-D поиском по таблице, и поэтому приводит к улучшаемой производительности симуляции.
По умолчанию все варианты блока реализуют настройку раны Уая для обмоток статора. Однако возможно переключиться на настройку раны дельты, выбираемое использование параметра Winding type. Когда в настройке раны дельты, фаза a соединяется между портами a и b, фазой b между портами b и c и фазой c между портами c и a.
Чтобы получить доступ к этим методам параметризации, щелкните правой кнопкой по блоку по своей модели, выберите Simscape> Block choices, и затем выберите желаемый вариант блока, с или без тепловых портов. По умолчанию тепловые порты не осушены. Для получения дополнительной информации смотрите Тепловые Порты.
В этой 2D модели данных потока поток, соединяющий каждую обмотку, принят, чтобы зависеть нелинейно только от тока в той же самой обмотке плюс угол ротора. На практике это - разумное предположение для многих постоянный магнит синхронные двигатели; однако, это менее точно для коммутируемых двигателей нежелания. Учитывая это предположение, потоки в этих трех обмотках:
где потокосцепление для A-фазы, вьющейся в зависимости от угла ротора и текущей A-фазы. Θ r = 0 соответствует ротору d- ось, выравнивающаяся с A-фазой положительное направление магнитного потока. M s является статором статора взаимная индуктивность.
Для улучшаемой числовой производительности уравнения, реализованные в блоке на самом деле, работают с частными производными потокосцепления относительно тока, , и угол ротора, , вместо потока непосредственно. Если ваш пакет FEM не экспортирует эти частные производные, можно определить их использующий скрипт MATLAB®. Смотрите Соленоид, Параметрированный с моделью Данных в качестве примера FEM и ее поддержкой скрипт MATLAB для примера того, как сделать это.
Электрические уравнения для блока, заданного в терминах частных производных потока:
где
v a, v b, v c является напряжениями, применился к A, B, и обмоткам статора C.
i a, i b, i c является токами статора в каждой из этих трех обмоток.
R s является сопротивлением каждой из обмоток статора.
M s является статором статора взаимная индуктивность.
частные производные потокосцепления относительно статора, текущего в каждой из этих трех обмоток.
частная производная потокосцепления относительно угла ротора.
Блок может автоматически вычислить матрицу крутящего момента от информации о потоке, которую вы предоставляете. В качестве альтернативы можно установить параметр Calculate torque matrix? на No и непосредственно задайте крутящий момент в зависимости от угла ротора и текущего. Смотрите страницу с описанием блока FEM-Parameterized Rotary Actuator для получения дополнительной информации.
В этой 2D модели данных потока поток, соединяющий каждую обмотку, принят, чтобы зависеть нелинейно от всего статора, извилистые токи, плюс он принят, что потокосцепление постоянного магнита синусоидальное. Внутренний магнит PMSMs (или IPMSMs) обычно соответствует этому предположению хорошо. Уравнения:
где
i d и i q является d- ось и q- токи оси, соответственно.
ϕ d и ϕ q является d- ось и q- потокосцепления оси, соответственно.
ϕ m является потокосцеплением постоянного магнита.
L d и L q является d- ось и q- составляющие индукции, соответственно. Они приняты, чтобы зависеть от d- ось и q- токи оси.
N является количеством пар полюса.
T является электрическим крутящим моментом.
Работа с четырехмерными данными имеет и стоимость эффективности симуляции и стоимость памяти. Чтобы уменьшать табличную размерность до 3D, 3-D Парк использования модели данных преобразовывает, чтобы сопоставить эти три тока с квадратурные токи и прямому:
В общем случае Парк преобразовывает карты к прямому, квадратуре и токам нулевой последовательности. Однако текущая нулевая последовательность обычно мала под нормальными условиями работы. Поэтому модель пропускает зависимость условий потокосцепления на текущей нулевой последовательности, и определяет потокосцепление в терминах только прямого и квадратурные токи плюс угол ротора. Уравнение потока для 3-D модели данных:
Электрические уравнения для блока также определены в терминах частных производных потока, похожих на 4-D модель данных. Можно вычислить 3-D данные о частной производной потокосцепления из 4-D использования данных о потокосцеплении ee_calculateFluxPartialDerivatives.
Поток, соединяющий каждую из обмоток, является функцией тока в той обмотке, токов в других двух обмотках и угла ротора. Для полной точности модель данных потока 4-D принимает, что потокосцепление является функцией этих трех токов и угла ротора, поэтому выполняя четырехмерный поиск по таблице. Уравнение потока:
где
ϕ a, ϕ b, ϕ c является потокосцеплениями для A, B, и обмотками статора C.
i a, i b, i c является токами статора в каждой из этих трех обмоток.
Θ r является углом ротора. Θ r = 0 соответствует случаю, где поток постоянного магнита выравнивается с потоком обмотки статора A-фазы.
N является количеством пар полюса.
Данные о потокосцеплении приняты циклические с Θ r. Если, например, двигатель имеет шесть пар полюса, то областью значений для данных является 0 ≤ Θ r ≤ 60 °. Необходимо обеспечить данные и в 0 и 60 градусах, и потому что данные являются циклическими, частные производные потокосцепления должны быть тем же самым в этих двух конечных точках.
Уравнение крутящего момента:
4-D модель данных не имеет опции для блока, чтобы определить крутящий момент из потокосцепления. Из-за увеличенных числовых издержек в 4-D случае лучше предварительно вычислить крутящий момент только однажды, вместо того, чтобы вычислить его каждый раз, когда вы запускаете симуляцию.
Для улучшаемой числовой производительности уравнения, реализованные в блоке на самом деле, работают с частными производными потокосцепления относительно этих трех токов и угла ротора, а не потока непосредственно. Если ваш пакет FEM не экспортирует эти частные производные, можно определить их использование ee_calculateFluxPartialDerivatives.
Электрические уравнения для блока, заданного в терминах частных производных потока:
где
v a, v b, v c является напряжениями, применился к A, B, и обмоткам статора C.
i a, i b, i c является токами статора в каждой из этих трех обмоток.
R s является сопротивлением каждой из обмоток статора.
3-D опции данных о потокосцеплении позволяют вам работать с необработанными данными о потокосцеплении, экспортированными из вашего моторного Design Tool конечного элемента (FE). Это в отличие от 3-D опций данных о частной производной, для которых необходимо определить частные производные. Можно обеспечить данные о потокосцеплении во множестве форматов, чтобы поддержать различные соглашения инструмента FE:
Плоские данные о потокосцеплении DQ-осей или данные о потокосцеплении A-фазы — поддержка инструментов Some, работающая с потокосцеплением, разрешенным в прямой (D) и квадратура (Q) оси. Преимущество этого подхода состоит в том, что данные для углов ротора в области значений 0 до 360/N/3 степеней требуются (где N является количеством пар полюса). Другие инструменты работают непосредственно с A-, B-и потокосцеплениями C-фазы, и для этого можно импортировать только потокосцепление A-фазы, для которого угловая область значений ротора должна быть в области значений 0 до 360/N степеней. Неявное предположение об импорте только данные A-фазы - то, что данные о фазе B и C являются тем же самым кроме переключенной на нижний регистр фазы.
Плоские использующие декартовы или полярные текущие координаты — Декартово табулирование подразумевает, что потокосцепление сведено в таблицу в терминах текущей D-оси и текущей Q-оси (плюс угол ротора). В качестве альтернативы полярное табулирование включает потокосцепления сведения в таблицу в терминах текущей величины, текущего угла усовершенствования относительно Q-оси и угла ротора. Преимущество полярных координат состоит в том, что это более естественно отражает разрешенные операционные токи, таким образом, избегая неиспользованных табличных точек данных.
Эти соглашения приводят к четырем опциям параметризации Flux linkage data format:
D and Q axes flux linkages as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta)
D and Q axes flux linkages as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta)
A-phase flux linkage as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta)
A-phase flux linkage as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta)
Помимо выбора формата данных потокосцепления, используемого вашим инструментом FE, необходимо выбрать версию Парка, преобразовывают используемый инструментом. Эти четыре соглашения описаны ниже и соответствуют этим четырем опциям для Park’s convention for tabulated data выпадающее меню.
Примечание
При рассмотрении регистрируемых значений для токов D-и Q-оси имейте в виду, что для каждой из этих опций, формат преобразован, по мере необходимости, так, чтобы внутренне блок FEM-Parameterized PMSM последовательно использовал Опцию 1.
Это - соглашение Парка, используемое внутренне блоками моторного и машины Simscape™ Electrical™. Все другие опции преобразованы в этот формат.
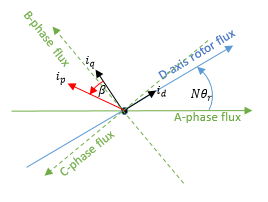
N: количество пар полюсов
θ r: угол ротора
i d, i q: D-ось и токи Q-оси
i p: Текущая величина =
β: Текущий угол усовершенствования =
Соответствующий Парк преобразовывает,
где i a, i b и i c является A-фаза, B-фаза и токи C-фазы, соответственно.
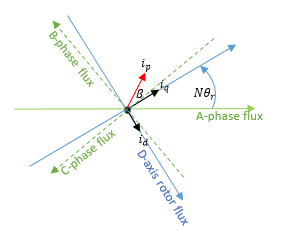
N: количество пар полюсов
θ r: угол ротора
i d, i q: D-ось и токи Q-оси
i p: Текущая величина =
β: Текущий угол усовершенствования =
Соответствующий Парк преобразовывает,
где i a, i b и i c является A-фаза, B-фаза и токи C-фазы, соответственно.
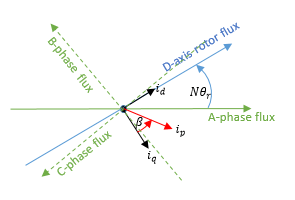
N: количество пар полюсов
θ r: угол ротора
i d, i q: D-ось и токи Q-оси
i p: Текущая величина =
β: Текущий угол усовершенствования =
Соответствующий Парк преобразовывает,
где i a, i b и i c является A-фаза, B-фаза и токи C-фазы, соответственно.
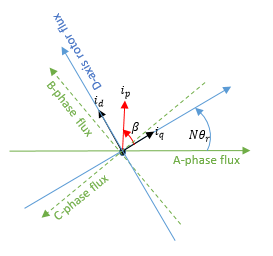
N: количество пар полюсов
θ r: угол ротора
i d, i q: D-ось и токи Q-оси
i p: Текущая величина =
β: Текущий угол усовершенствования =
Соответствующий Парк преобразовывает,
где i a, i b и i c является A-фаза, B-фаза и токи C-фазы, соответственно.
Потери в железе моделей блока FEM-Parameterized PMSM согласно методам параметризации вы выбираете для потока и крутящего момента.
Для 2-D partial derivative data, 3-D partial derivative data и опций 4-D partial derivative data, с или без тепловых портов, модель потери в железе основана на работе Меллора [1]. Потери в железе разделены на два условия, одно представление основного пути к намагничиванию и другое представление перекрестного зубного пути к совету, который становится активным во время ослабленной операции поля.
Термин, представляющий основной путь к намагничиванию, зависит от вызванного напряжения статора RMS, :
Это - доминирующий термин в течение операции без загрузок. k является коэффициентом противо-ЭДС, постоянной, связывающим вольты RMS на Гц. Это задано как , где f является электрической частотой. Первый срок на правой стороне является магнитной гистерезисной потерей, второй является потеря токов Фуко, и третьей является избыточная потеря. Эти три коэффициента, появляющиеся на числителях, выведены из значений, что вы предусматриваете гистерезис разомкнутой цепи, вихрь и избыточные потери.
Термин, представляющий перекрестный зубной путь к совету, становится важным, когда поле размагничивания создано и может быть определено из теста короткой схемы анализа конечных элементов. Это зависит от эдс RMS, сопоставленной с перекрестным зубным потоком совета, :
Три условия числителя выведены из значений, вы предусматриваете гистерезис короткой схемы, вихрь и избыточные потери.
Для 3-D flux linkage data с или без тепловых портов, можно также смоделировать потери в железе на основе уравнения Steinmetz. Метод Steinmetz масштабируется для различных частот вращения двигателя или электрических частот так, чтобы данные о потере в железе только требовались как функция моторных токов. Если вы устанавливаете параметр Iron losses modeling на Specify open and short circuit loss data (permanent magnet motors only), блок использует метод Steinmetz, но принимает постоянные коэффициенты и никакую зависимость от максимального тока и текущего усовершенствования фазы. С другой стороны, если вы устанавливаете параметр Flux linkage data format на любой D and Q axes flux linkages as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta) или A-phase flux linkage as a function of peak current magnitude (I), current advance angle (B), and rotor angle (theta) , затем блок свел в таблицу коэффициенты с Peak current magnitude vector, I и параметрами Current advance angle vector, B, так, чтобы потерями в железе дали:
где:
f является электрической частотой в Hz.
khr(Ip,β) является Rotor hysteresis loss coefficient, k_hr(I,B).
kJr(Ip,β) является Rotor eddy current loss coefficient, k_Jr(I,B).
ker(Ip,β) является Rotor excess current loss coefficient, k_er(I,B).
khs(Ip,β) является Stator hysteresis loss coefficient, k_hs(I,B).
kJs(Ip,β) является Stator eddy current loss coefficient, k_Js(I,B).
kes(Ip,β) является Stator excess current loss coefficient, k_es(I,B).
Точно так же, если вы устанавливаете параметр Flux linkage data format на любой D and Q axes flux linkages as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta) или A-phase flux linkage as a function of D-axis current (iD), Q-axis current (iQ), and rotor angle (theta), затем потерями в железе дают:
где:
khr(iD,iQ) является Rotor hysteresis loss coefficient, k_hr(iD,iQ).
kJr(iD,iQ) является Rotor eddy current loss coefficient, k_Jr(iD,iQ).
ker(iD,iQ) является Rotor excess current loss coefficient, k_er(iD,iQ).
khs(iD,iQ) является Stator hysteresis loss coefficient, k_hs(iD,iQ).
kJs(iD,iQ) является Stator eddy current loss coefficient, k_Js(iD,iQ).
kes(iD,iQ) является Stator excess current loss coefficient, k_es(iD,iQ).
Блок имеет четыре дополнительных тепловых порта, один для каждой из этих трех обмоток и один для ротора. Эти порты скрыты по умолчанию. Чтобы осушить тепловые порты, щелкните правой кнопкой по блоку по своей модели, выберите Simscape> Block choices, и затем выберите желаемый вариант блока с тепловыми портами: 2-D partial derivative data | Show thermal port, 3-D partial derivative data | Show thermal port, 4-D partial derivative data | Show thermal port или 3-D flux linkage data | Show thermal port. Это действие отображает тепловые порты на значке блока и отсоединяет параметры Thermal Port и Temperature Dependence. Эти параметры описаны далее на этой странице с описанием.
Используйте тепловые порты, чтобы симулировать эффекты медного сопротивления и потерь в железе, которые преобразовывают электроэнергию в теплоту. Для получения дополнительной информации об использовании тепловых портов в блоках привода смотрите Термальные эффекты Симуляции во Вращательных и Поступательных Приводах.
Этот блок имеет нижеследующие ограничения:
Для модели 2D данных статор статора взаимная индуктивность, заданная значением параметров Stator mutual inductance, Ms, является постоянной в процессе моделирования и не меняется в зависимости от угла ротора. Это означает, что блок подходит для моделирования большей части PMSM и бесщеточных двигателей постоянного тока, но не переключенных двигателей нежелания.
3-D и 4-D модели данных принимают симметрию, так, чтобы зависимость от потокосцепления от токов и угла ротора для обмоток B и C могла быть определена из этого для обмотки A.
Для 4-D модели данных рассмотрите требования к памяти при фиксации независимых значений параметров (три тока и углы ротора). Опция линейной интерполяции использует меньше памяти, но опция сплайн-интерполяции более точна для данного независимого интервала параметра.
Модель потерь в железе принимает синусоидальные токи.
[1] Меллор, P.H., Р. Робель и Д. Холидей. “В вычислительном отношении эффективная модель потери в железе для бесщеточных машин AC, которая обслуживает расчетный поток и поле, ослабила операцию”. IEEE Электрическая Конференция по Машинам и Дискам. Май 2009.
ee_calculateFluxPartialDerivatives | FEM-Parameterized Linear Actuator | FEM-Parameterized Rotary Actuator