factoran

Факторный анализ

свернуть все на странице

Синтаксис

lambda = factoran(X,m)

[lambda,psi] = factoran(X,m)

[lambda,psi,T] = factoran(X,m)

[lambda,psi,T,stats] = factoran(X,m)

[lambda,psi,T,stats,F] = factoran(X,m)

___ = factoran(X,m,Name,Value)

Описание

factoran вычисляет оценку наибольшего правдоподобия (MLE) матрицы факторных нагрузок Λ в модели факторного анализа

$x = μ + Λ f + e$

где x является вектором из наблюдаемых переменных, μ является постоянным вектором из средних значений, Λ является постоянный d- m матрица факторных нагрузок, f является вектором из независимых, стандартизированных общих множителей, и e является вектором из независимых специфических факторов. x, μ и e у каждого есть длина d. f имеет длину m.

В качестве альтернативы модель факторного анализа может быть задана как

$cov (x) = Λ Λ^{T} + Ψ$

где $Ψ = cov (e)$ d- d диагональная матрица определенных отклонений.

Для использования factoran и его отношение к pca, смотрите Выполняют Факторный анализ Классов Экзамена.

пример

lambda = factoran(X,m) возвращает матрицу факторных нагрузок lambda для матрицы данных X с m общие множители.

пример

[lambda,psi] = factoran(X,m) также возвращает оценки наибольшего правдоподобия определенных отклонений.

пример

[lambda,psi,T] = factoran(X,m) также возвращает m- m матрица вращения факторных нагрузок T.

пример

[lambda,psi,T,stats] = factoran(X,m) также возвращает структуру stats содержа информацию, относящуюся к нулевой гипотезе _H0, что количеством общих множителей является m.

пример

[lambda,psi,T,stats,F] = factoran(X,m) также возвращает предсказания общих множителей (факторные баллы).

пример

___ = factoran(X,m,Name,Value) изменяет подгонку модели и выходные параметры с помощью одного или нескольких аргументов пары "имя-значение", для любых выходных аргументов в предыдущих синтаксисах. Например, можно указать что X данные являются ковариационной матрицей.

Примеры

свернуть все

Факторный анализ искусственных данных

Скрипт Open Live Script

Создайте некоторые псевдослучайные необработанные данные.

rng default % For reproducibility
n = 100;
X1 = 5 + 3*rand(n,1); % Factor 1
X2 = 20 - 5*rand(n,1); % Factor 2

Создайте шесть векторов данных из необработанных данных и добавьте случайный шум.

Y1 = 2*X1 + 3*X2 + randn(n,1);
Y2 = 4*X1 + X2 + 2*randn(n,1);
Y3 = X1 - X2 + 3*randn(n,1);
Y4 = -2*X1 + 4*X2 + 4*randn(n,1);
Y5 = 3*(X1 + X2) + 5*randn(n,1);
Y6 = X1 - X2/2 + 6*randn(n,1);

Создайте матрицу данных из векторов данных.

X = [Y1,Y2,Y3,Y4,Y5,Y6];

Извлеките эти два фактора из матрицы зашумленных данных X использование factoran. Отобразите выводы.

m = 2;
[lambda,psi,T,stats,F] = factoran(X,m);
disp(lambda)

    0.8666    0.4828
    0.8688   -0.0998
   -0.0131   -0.5412
    0.2150    0.8458
    0.7040    0.2678
   -0.0806   -0.2883

disp(psi)

disp(T)

    0.8728    0.4880
    0.4880   -0.8728

disp(stats)

    loglike: -0.0531
        dfe: 4
      chisq: 5.0335
          p: 0.2839

disp(F(1:10,:))

    1.8845   -0.6568
   -0.1714   -0.8113
   -1.0534    2.0743
    1.0390   -1.1784
    0.4309    0.9907
   -1.1823    0.6570
   -0.2129    1.1898
   -0.0844   -0.7421
    0.5854   -1.1379
    0.8279   -1.9624

Просмотрите корреляционную матрицу данных.

corrX = corr(X)

corrX = 6×6

    1.0000    0.7047   -0.2710    0.5947    0.7391   -0.2126
    0.7047    1.0000    0.0203    0.1032    0.5876    0.0289
   -0.2710    0.0203    1.0000   -0.4793   -0.1495    0.1450
    0.5947    0.1032   -0.4793    1.0000    0.3752   -0.2134
    0.7391    0.5876   -0.1495    0.3752    1.0000   -0.2030
   -0.2126    0.0289    0.1450   -0.2134   -0.2030    1.0000

Сравните corrX к его соответствующим значениям, возвращенным factoran, lambda*lambda' + diag(psi).

C0 = lambda*lambda' + diag(psi)

C0 = 6×6

    1.0000    0.7047   -0.2726    0.5946    0.7394   -0.2091
    0.7047    1.0000    0.0426    0.1023    0.5849   -0.0413
   -0.2726    0.0426    1.0000   -0.4605   -0.1542    0.1571
    0.5946    0.1023   -0.4605    1.0000    0.3779   -0.2611
    0.7394    0.5849   -0.1542    0.3779    1.0000   -0.1340
   -0.2091   -0.0413    0.1571   -0.2611   -0.1340    1.0000

factoran получает lambda и psi это соответствует тесно корреляционной матрице исходных данных.

Просмотрите результаты, не используя вращение.

[lambda,psi,T,stats,F] = factoran(X,m,'Rotate','none');
disp(lambda)

    0.9920    0.0015
    0.7096    0.5111
   -0.2755    0.4659
    0.6004   -0.6333
    0.7452    0.1098
   -0.2111    0.2123

disp(psi)

disp(T)

     1     0
     0     1

disp(stats)

    loglike: -0.0531
        dfe: 4
      chisq: 5.0335
          p: 0.2839

disp(F(1:10,:))

    1.3243    1.4929
   -0.5456    0.6245
    0.0928   -2.3246
    0.3318    1.5356
    0.8596   -0.6544
   -0.7114   -1.1504
    0.3947   -1.1424
   -0.4358    0.6065
   -0.0444    1.2789
   -0.2350    2.1169

Вычислите факторы с помощью только ковариационную матрицу X.

X2 = cov(X);
[lambda2,psi2,T2,stats2] = factoran(X2,m,'Xtype','covariance','Nobs',n)

lambda2 = 6×2

    0.8666    0.4828
    0.8688   -0.0998
   -0.0131   -0.5412
    0.2150    0.8458
    0.7040    0.2678
   -0.0806   -0.2883

T2 = 2×2

    0.8728    0.4880
    0.4880   -0.8728

stats2 = struct with fields:
    loglike: -0.0531
        dfe: 4
      chisq: 5.0335
          p: 0.2839

Результаты эквивалентны с необработанными данными, кроме factoran не может вычислить факторную матрицу баллов F для данных о ковариации.

Оцените и постройте факторные нагрузки

Скрипт Open Live Script

Загрузите выборочные данные.

load carbig

Задайте переменную матрицу.

X = [Acceleration Displacement Horsepower MPG Weight]; 
X = X(all(~isnan(X),2),:);

Оцените факторные нагрузки с помощью минимального предсказания среднеквадратической ошибки для факторного анализа с двумя общими множителями.

[Lambda,Psi,T,stats,F] = factoran(X,2,'Scores','regression');
inv(T'*T);   % Estimated correlation matrix of F, == eye(2)
Lambda*Lambda' + diag(Psi); % Estimated correlation matrix
Lambda*inv(T);              % Unrotate the loadings
F*T';                       % Unrotate the factor scores

Создайте побочную сюжетную линию двух факторов.

biplot(Lambda,'LineWidth',2,'MarkerSize',20)

Figure contains an axes. The axes contains 11 objects of type line.

Оцените факторные нагрузки с помощью ковариации (или корреляция) матрица.

[Lambda,Psi,T] = factoran(cov(X),2,'Xtype','covariance')

Lambda = 5×2

   -0.2432   -0.8500
    0.8773    0.3871
    0.7618    0.5930
   -0.7978   -0.2786
    0.9692    0.2129

T = 2×2

    0.9476    0.3195
    0.3195   -0.9476

(Вы могли вместо этого использовать corrcoef(X) вместо cov(X) создать данные для factoran.) Несмотря на то, что оценки являются тем же самым, использование ковариационной матрицы, а не необработанных данных препятствует тому, чтобы вы запросили уровень значения или баллы.

Используйте промакс. вращение.

[Lambda,Psi,T,stats,F] = factoran(X,2,'Rotate','promax','power',4);
inv(T'*T)                            % Estimated correlation of F, no longer eye(2)

ans = 2×2

    1.0000   -0.6391
   -0.6391    1.0000

Lambda*inv(T'*T)*Lambda'+diag(Psi)   % Estimated correlation of X

ans = 5×5

    1.0000   -0.5424   -0.6893    0.4309   -0.4167
   -0.5424    1.0000    0.8979   -0.8078    0.9328
   -0.6893    0.8979    1.0000   -0.7730    0.8647
    0.4309   -0.8078   -0.7730    1.0000   -0.8326
   -0.4167    0.9328    0.8647   -0.8326    1.0000

Постройте невращаемые переменные с наклонными наложенными осями.

invT = inv(T);
Lambda0 = Lambda*invT;
figure()
line([-invT(1,1) invT(1,1) NaN -invT(2,1) invT(2,1)], ...
     [-invT(1,2) invT(1,2) NaN -invT(2,2) invT(2,2)], ...
     'Color','r','LineWidth',2)
grid on
hold on
biplot(Lambda0,'LineWidth',2,'MarkerSize',20)       
xlabel('Loadings for unrotated Factor 1')
ylabel('Loadings for unrotated Factor 2')

Figure contains an axes. The axes contains 11 objects of type line.

Постройте вращаемые переменные против наклонных осей.

figure()
biplot(Lambda,'LineWidth',2,'MarkerSize',20)

Figure contains an axes. The axes contains 11 objects of type line.

Входные параметры

свернуть все

`X` данные
матрица

Данные в виде n- d матрица, где каждая строка является наблюдением за d переменные.

Типы данных: double

`m` — Количество общих множителей
положительное целое число

Количество общих множителей в виде положительного целого числа.

Пример 3

Типы данных: double

Аргументы в виде пар имя-значение

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: lambda = factoran(X,m,'Start',10,'Scores','Thomson') задает, чтобы использовать начальную точку для определенных отклонений 10 и Томсоновский метод для предсказания факторных баллов.

`'Xtype'` — Тип входных данных
`'data'` (значение по умолчанию) | `'covariance'`

Тип входных данных XВ виде разделенной запятой пары, состоящей из 'Xtype' и одно из следующего:

'data' X необработанные данные.
'covariance' X положительная определенная ковариация или корреляционная матрица.

Пример: 'Xtype','covariance'

Типы данных: char | string

`'Scores'` — Метод для предсказания факторных баллов
`'wls'` или эквивалентный `'Bartlett'` (значение по умолчанию) | `'regression'` или эквивалентный `'Thomson'`

Метод для предсказания факторных баллов в виде разделенной запятой пары, состоящей из 'Scores' и одно из следующего:

'wls' или эквивалентный 'Bartlett' — Метод взвешенных наименьших квадратов оценивает обработку F как зафиксировано
'regression' или эквивалентный 'Thomson' — Минимальное предсказание среднеквадратической ошибки, которое эквивалентно гребенчатой регрессии

Пример: 'Scores','regression'

Типы данных: char | string

`'Start'` — Начальная точка для определенных отклонений `psi` в оптимизации наибольшего правдоподобия
`'Rsquared'` (значение по умолчанию) | `'random'` | положительное целое число | матрица с `d` 'Строки'

Начальная точка для определенных отклонений psi в оптимизации наибольшего правдоподобия в виде разделенной запятой пары, состоящей из 'Start' и одно из следующего:

'Rsquared' — Выбирает стартовый вектор в качестве масштабного коэффициента времена diag(inv(corrcoef(X))) (значение по умолчанию). Для примеров смотрите Jöreskog [2].
'random' — Выбирает d равномерно распределенные значения на интервале [0,1].
Положительное целое число — Выполняет возмущенное количество наибольшего правдоподобия, каждый инициализированный таким же образом как 'random'. factoran возвращает подгонку с самой высокой вероятностью.
Матрица с d строки — Выполняют одно наибольшее правдоподобие, подходящее для каждого столбца заданной матрицы. factoran инициализирует iоптимизация th со значениями от iстолбец th.

Пример: 'Start',5

Типы данных: double | char | string

`'Rotate'` — Метод раньше вращал факторные нагрузки и баллы
`'varimax'` (значение по умолчанию) | `'none'` | `'quartimax'` | `'equamax'` | `'parsimax'` | `'orthomax'` | `'promax'` | `'procrustes'` | `'pattern'` | указатель на функцию

Метод раньше вращал факторные нагрузки и баллы в виде разделенной запятой пары, состоящей из 'Rotate' и одно из значений в следующей таблице. Можно управлять вращением путем определения дополнительных аргументов пары "имя-значение" rotatefactors функция, как описано в таблице. Для получения дополнительной информации смотрите rotatefactors.

Значение	Описание
`'none'`	Не выполняет вращения
`'equamax'`	Особый случай `'orthomax'` вращение. Используйте `'normalize''RelTol'` , и `'maxit'` аргументы, чтобы управлять деталями вращения.
`'orthomax'`	Ортогональное вращение, которое максимизирует критерий на основе отклонения загрузок. Используйте `'coeff'`, `'normalize''RelTol'` , и `'maxit'` аргументы, чтобы управлять деталями вращения.
`'parsimax'`	Особый случай ортомакс. вращения. Используйте `'normalize''RelTol'` , и `'maxit'` аргументы, чтобы управлять деталями вращения.
`'pattern'`	Выполняет любого наклонное вращение (значение по умолчанию) или ортогональное вращение, чтобы лучше всего совпадать с заданной матрицей шаблона. Используйте `'type'` аргумент, чтобы выбрать тип вращения. Используйте `'target'` аргумент, чтобы задать матрицу шаблона.
`'procrustes'`	Выполняет любого наклонное вращение (значение по умолчанию) или ортогональное вращение, чтобы лучше всего совпадать с заданной целевой матрицей в смысле наименьших квадратов. Используйте `'type'` аргумент, чтобы выбрать тип вращения. Используйте `'target'` аргумент, чтобы задать целевую матрицу.
`'promax'`	Выполняет наклонное procrustes вращение к целевой матрице, определенной `factoran` в зависимости от ортомакс. решения. Используйте `'power'` аргумент, чтобы задать экспоненту для создания целевой матрицы. Поскольку `'promax'` использование `'orthomax'` внутренне, можно также задать аргументы, которые применяются `к 'orthomax'`.
`'quartimax'`	Особый случай `'orthomax'` вращение. Используйте `'normalize''RelTol'` , и `'maxit'` аргументы, чтобы управлять деталями вращения.
`'varimax'`	Особый случай `'orthomax'` вращение (значение по умолчанию). Используйте `'normalize''RelTol'` , и `'maxit'` аргументы, чтобы управлять деталями вращения.
указатель на функцию	Указатель на функцию к функции вращения формы [B,T] = myrotation(A,...) где `A` `d`- `m` матрица невращаемых факторных нагрузок, `B` `d`- `m` матрица вращаемых загрузок и `T` соответствующий `m`- `m` матрица вращения. Используйте `factoran` аргумент `'UserArgs'` передать дополнительные аргументы этой функции вращения. Смотрите Пользовательскую Функцию Вращения.

Пример: [lambda,psi,T] = factoran(X,m,'Rotate','promax','power',5,'maxit',100)

Типы данных: char | string | function_handle

`'Delta'` — Нижняя граница для `psi` во время оптимизации наибольшего правдоподобия
0.005 (значение по умолчанию) | скаляр между 0 и 1

Нижняя граница для psi аргумент во время оптимизации наибольшего правдоподобия в виде разделенной запятой пары, состоящей из 'Delta' и скалярное значение между 0 и 1 (0 <Delta < 1).

Пример: 0.02

Типы данных: double

`'OptimOpts'` — Опции для оптимизации наибольшего правдоподобия
`[]` (значение по умолчанию) | структура создается `statset`

Опции для оптимизации наибольшего правдоподобия в виде разделенной запятой пары, состоящей из 'OptimOpts' и структура создается statset. Можно ввести statset('factoran') для списка опций, которые также описаны в следующей таблице.

Имя поля (`statset` аргумент)	Значение	Значение {значение по умолчанию}
`'Display'`	Объем информации отображен алгоритмом	`{'off'}` — Отображения никакая информация `'final'` — Отображает окончательный вывод `'iter'` — Отображает итеративный вывод к командному окну для некоторых функций; в противном случае отображает окончательный вывод
`MaxFunEvals`	Максимальное количество оценок целевой функции позволено	Положительное целое число, `{400}`
`MaxIter`	Максимальное количество итераций позволено	Положительное целое число, `{100}`
`TolFun`	Допуск завершения к значению целевой функции. Решатель останавливается, когда последовательные значения функции меньше `TolFun` независимо.	Положительная скалярная величина, `{1e-8}`
`TolX`	Допуск завершения к параметрам. Решатель останавливается, когда последовательные значения параметров меньше `TolX` независимо.	Положительная скалярная величина, `{1e-8}`

Пример: statset('Display','iter')

Типы данных: struct

`'Nobs'` — Количество наблюдений раньше оценивало `X`
положительное целое число

Количество наблюдений раньше оценивало XВ виде разделенной запятой пары, состоящей из 'Nobs' и положительное целое число. Nobs применяется только когда Xtype 'covariance'. Определение 'Nobs' позволяет вам получить stats поля chisq структуры output и p.

Пример: 50

Типы данных: double

Выходные аргументы

свернуть все

`lambda` — Факторные нагрузки
матрица

Факторные нагрузки, возвращенные как d- m матрица. d количество столбцов матрицы данных X, и m второй входной параметр factoran.

(i,j)элемент th lambda коэффициент или загрузка, jфактор th для iпеременная th. По умолчанию, factoran вызывает функциональный rotatefactors вращать предполагаемые факторные нагрузки с помощью 'varimax' опция. Для получения информации о вращении смотрите Вращение Факторных нагрузок и Баллов.

`psi` — Определенные отклонения
вектор

Определенные дисперсии, возвращенные как d- 1 вектор. d количество столбцов матрицы данных X. Записи psi оценки наибольшего правдоподобия.

`T` — Вращение факторных нагрузок
матрица

Вращение факторных нагрузок, возвращенное как m- m матрица. m второй входной параметр factoran. Для получения информации о вращении смотрите Вращение Факторных нагрузок и Баллов.

`stats` — Информация об общих множителях
структура

Информация об общих множителях, возвращенных как структура. stats содержит информацию, относящуюся к нулевой гипотезе _H0, что количеством общих множителей является m.

stats содержит следующие поля.

Поле	Описание
`loglike`	Максимизируемое значение логарифмической правдоподобности
`dfe`	Ошибочные степени свободы = `((d-m)^2 - (d+m))/2`
`chisq`	Аппроксимируйте статистическую величину в квадрате хи для нулевой гипотезы
`p`	Уровень значения правильного хвоста для нулевой гипотезы

factoran не вычисляет chisq и p поля, если dfe положительно и все определенные оценки отклонения в psi положительны (см. Случай Хейвуда). Если X ковариационная матрица, и вы хотите factoran вычислить chisq и p поля, затем необходимо также задать 'Nobs' аргумент пары "имя-значение".

`F` — Факторные баллы
матрица

Факторные баллы, также названные предсказаниями общих множителей, возвратились как n- m матрица. n количество строк в матрице данных X, и m второй входной параметр factoran.

Примечание

Если X ковариационная матрица (Xtype = 'covariance'), factoran не может вычислить F.

factoran вращает F использование того же критерия что касается lambda. Для получения информации о вращении смотрите Вращение Факторных нагрузок и Баллов.

Больше о

свернуть все

Случай Хейвуда

Если элементы psi равны значению Delta параметр (то есть, они - по существу нуль), подгонка известна как случай Хейвуда, и интерпретация получившихся оценок проблематична. В частности, может быть несколько локальных максимумов вероятности, каждого с различными оценками загрузок и определенных отклонений. Случаи Хейвуда могут указать на сверхподбор кривой (m является слишком большим), но может также быть результат underfitting.

Вращение факторных нагрузок и баллов

Если вы явным образом не задаете вращения с помощью 'Rotate' аргумент пары "имя-значение", factoran вращает предполагаемые факторные нагрузки lambda и факторные баллы F. Выходная матрица T используется, чтобы вращать загрузки, то есть, lambda = lambda0*T, где lambda0 начальная буква (невращаемый) MLE загрузок. T ортогональная матрица для ортогональных вращений и единичная матрица ни для какого вращения. Инверсия T известен как первичную матрицу вращения оси, тогда как T самостоятельно связан со ссылочной матрицей вращения оси. Для ортогональных вращений эти два идентичны.

factoran вычисляет факторные баллы, которые вращались inv(T'), то есть, F = F0 * inv(T'), где F0 содержит невращаемые предсказания. Предполагаемая ковариация F inv(T'*T), который является единичной матрицей для ортогонального или никакого вращения. Вращение факторных нагрузок и баллов является попыткой создать структуру, которую легче интерпретировать в матрице загрузок после оценки наибольшего правдоподобия.

Пользовательская функция вращения

Синтаксис для передачи дополнительных аргументов к пользовательской функции вращения:

[Lambda,Psi,T] = ...
     factoran(X,2,'Rotate',@myrotation,'UserArgs',1,'two');

Ссылки

[1] Харман, Гарри Гораций. Современный факторный анализ. 3-й Эд. Чикаго: нажатие Чикагского университета, 1976.

[2] Jöreskog, K. G. “Некоторые Вклады в Факторный анализ Наибольшего правдоподобия”. Psychometrika 32, № 4 (декабрь 1967): 443–82. https://doi.org/10.1007/BF02289658

[3] Lawley, D. N. и А. Э. Максвелл. Факторный анализ как статистический метод. 2-й Эд. Нью-Йорк: American Elsevier Publishing Co., 1971.

Расширенные возможности

"Высокие" массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

pcacov и factoran не работайте непосредственно над длинными массивами. Вместо этого используйте C = gather(cov(X)) вычислить ковариационную матрицу длинного массива. Затем можно использовать pcacov или factoran работать над ковариационной матрицей в оперативной памяти. В качестве альтернативы можно использовать pca непосредственно на длинном массиве.

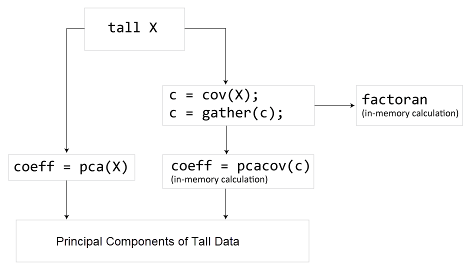
Для получения дополнительной информации смотрите Длинные массивы для Данных, которые не помещаются в память.

Темы

Представлено до R2006a

Документация

factoran

Синтаксис

Описание

Примеры

Факторный анализ искусственных данных

Оцените и постройте факторные нагрузки

Входные параметры

`X` данные
матрица

`m` — Количество общих множителей
положительное целое число

Аргументы в виде пар имя-значение

`'Xtype'` — Тип входных данных
`'data'` (значение по умолчанию) | `'covariance'`

`'Scores'` — Метод для предсказания факторных баллов
`'wls'` или эквивалентный `'Bartlett'` (значение по умолчанию) | `'regression'` или эквивалентный `'Thomson'`

`'Delta'` — Нижняя граница для `psi` во время оптимизации наибольшего правдоподобия
0.005 (значение по умолчанию) | скаляр между 0 и 1

`'OptimOpts'` — Опции для оптимизации наибольшего правдоподобия
`[]` (значение по умолчанию) | структура создается `statset`

`'Nobs'` — Количество наблюдений раньше оценивало `X`
положительное целое число

Выходные аргументы

`lambda` — Факторные нагрузки
матрица

`psi` — Определенные отклонения
вектор

`T` — Вращение факторных нагрузок
матрица

`stats` — Информация об общих множителях
структура

`F` — Факторные баллы
матрица

Больше о

Случай Хейвуда

Вращение факторных нагрузок и баллов

Пользовательская функция вращения

Ссылки

Расширенные возможности

"Высокие" массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Смотрите также

Темы

Документация Statistics and Machine Learning Toolbox

Поддержка

Документация

factoran

Синтаксис

Описание

Примеры

Факторный анализ искусственных данных

Оцените и постройте факторные нагрузки

Входные параметры

X данные матрица

m — Количество общих множителей положительное целое число

Аргументы в виде пар имя-значение

'Xtype' — Тип входных данных 'data' (значение по умолчанию) | 'covariance'

'Scores' — Метод для предсказания факторных баллов 'wls' или эквивалентный 'Bartlett' (значение по умолчанию) | 'regression' или эквивалентный 'Thomson'

'Rotate' — Метод раньше вращал факторные нагрузки и баллы 'varimax' (значение по умолчанию) | 'none' | 'quartimax' | 'equamax' | 'parsimax' | 'orthomax' | 'promax' | 'procrustes' | 'pattern' | указатель на функцию

'Delta' — Нижняя граница для psi во время оптимизации наибольшего правдоподобия0.005 (значение по умолчанию) | скаляр между 0 и 1

'OptimOpts' — Опции для оптимизации наибольшего правдоподобия [] (значение по умолчанию) | структура создается statset

'Nobs' — Количество наблюдений раньше оценивало X положительное целое число

Выходные аргументы

lambda — Факторные нагрузки матрица

psi — Определенные отклонения вектор

T — Вращение факторных нагрузок матрица

stats — Информация об общих множителях структура

F — Факторные баллы матрица

Больше о

Случай Хейвуда

Вращение факторных нагрузок и баллов

Пользовательская функция вращения

Ссылки

Расширенные возможности

"Высокие" массивы Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Смотрите также

Темы

Документация Statistics and Machine Learning Toolbox

Поддержка

`X` данные
матрица

`m` — Количество общих множителей
положительное целое число

`'Xtype'` — Тип входных данных
`'data'` (значение по умолчанию) | `'covariance'`

`'Scores'` — Метод для предсказания факторных баллов
`'wls'` или эквивалентный `'Bartlett'` (значение по умолчанию) | `'regression'` или эквивалентный `'Thomson'`

`'Delta'` — Нижняя граница для `psi` во время оптимизации наибольшего правдоподобия
0.005 (значение по умолчанию) | скаляр между 0 и 1

`'OptimOpts'` — Опции для оптимизации наибольшего правдоподобия
`[]` (значение по умолчанию) | структура создается `statset`

`'Nobs'` — Количество наблюдений раньше оценивало `X`
положительное целое число

`lambda` — Факторные нагрузки
матрица

`psi` — Определенные отклонения
вектор

`T` — Вращение факторных нагрузок
матрица

`stats` — Информация об общих множителях
структура

`F` — Факторные баллы
матрица

"Высокие" массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.