Этот раздел берет вас через функции 1D критически произведенного анализа вейвлета с помощью программного обеспечения Wavelet Toolbox™.
Тулбокс обеспечивает эти функции для 1D анализа сигнала. Для получения дополнительной информации смотрите страницы с описанием.
В этом разделе вы будете учиться как
Загрузите сигнал
Выполните одноуровневое разложение вейвлета сигнала
Создайте приближения и детали от коэффициентов
Отобразите приближение и деталь
Регенерируйте сигнал обратным вейвлетом, преобразовывают
Выполните многоуровневое разложение вейвлета сигнала
Извлеките приближение и детализируйте коэффициенты
Восстановите приближение уровня 3
Восстановите уровень 1, 2 и 3 детали
Отобразите результаты многоуровневого разложения
Восстановите исходный сигнал от разложения уровня 3
Удалите шум из сигнала
Совершенствуйте анализ
Сожмите сигнал
Покажите статистику и гистограммы сигнала
Поскольку можно выполнить исследования или из командной строки или из использования приложения Wavelet Analyzer, этот раздел имеет подразделы, покрывающие каждый метод.
Итоговый подраздел обсуждает, как обмениваться сигналом и информацией о коэффициенте между диском и графическими инструментами.
Этот пример включает реальный сигнал — электрическое потребление, измеренное в течение 3 дней. Этот сигнал особенно интересен из-за шума, введенного, когда дефект, разработанный в оборудовании контроля как измерения, делался. Анализ вейвлета эффективно удаляет шум.
Примечание
К denoise сигнал, wdenoise и Wavelet Signal Denoiser рекомендуется.
Загрузите сигнал и выберите фрагмент для анализа вейвлета.
load leleccum;
s = leleccum(1:3920);
l_s = length(s);Выполните одноуровневое разложение вейвлета сигнала.
Выполните одноуровневое разложение сигнала с помощью db1 вейвлет.
[cA1,cD1] = dwt(s,'db1');Это генерирует коэффициенты приближения уровня 1 (cA1) и деталь (cD1).
Создайте приближения и детали от коэффициентов.
Создать приближение уровня 1 и деталь (A1 и D1) от коэффициентов cA1 и cD1Ввод
A1 = upcoef('a',cA1,'db1',1,l_s); D1 = upcoef('d',cD1,'db1',1,l_s);
или
A1 = idwt(cA1,[],'db1',l_s); D1 = idwt([],cD1,'db1',l_s);
Отобразите приближение и деталь.
Чтобы отобразить результаты уровня одно разложение, ввести
subplot(1,2,1); plot(A1); title('Approximation A1') subplot(1,2,2); plot(D1); title('Detail D1')
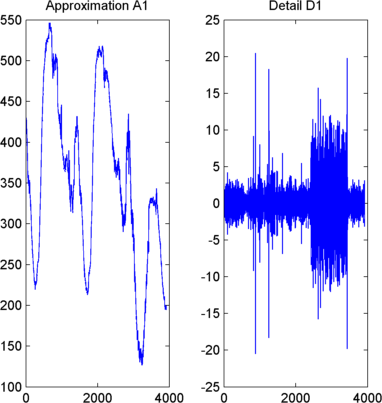
Регенерируйте сигнал при помощи Обратного Преобразования Вейвлета.
Чтобы найти обратное преобразование, войти
A0 = idwt(cA1,cD1,'db1',l_s);
err = max(abs(s-A0))Выполните многоуровневое разложение вейвлета сигнала.
Выполнять разложение уровня 3 сигнала (снова использование db1 вейвлет), ввести
[C,L] = wavedec(s,3,'db1');Коэффициенты всех компонентов дважды косвенного разложения (то есть, дважды косвенного приближения и первых трех уровней детализации) возвращены конкатенированные в один вектор, C. Вектор L дает длины каждого компонента.
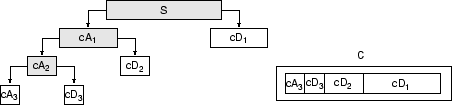
Извлеките приближение и детализируйте коэффициенты.
Извлекать коэффициенты приближения уровня 3 из CВвод
cA3 = appcoef(C,L,'db1',3);
Извлекать уровни 3, 2 и 1 коэффициент детали от CВвод
cD3 = detcoef(C,L,3); cD2 = detcoef(C,L,2); cD1 = detcoef(C,L,1);
или
[cD1,cD2,cD3] = detcoef(C,L,[1,2,3]);
Восстановите приближение Уровня 3 и Уровень 1, 2 и 3 детали.
Восстановить приближение уровня 3 от CВвод
A3 = wrcoef('a',C,L,'db1',3);
Восстановить детали на уровнях 1, 2, и 3, от CВвод
D1 = wrcoef('d',C,L,'db1',1);
D2 = wrcoef('d',C,L,'db1',2);
D3 = wrcoef('d',C,L,'db1',3);
Отобразите результаты многоуровневого разложения.
Чтобы отобразить результаты разложения уровня 3, ввести
subplot(2,2,1); plot(A3);
title('Approximation A3')
subplot(2,2,2); plot(D1);
title('Detail D1')
subplot(2,2,3); plot(D2);
title('Detail D2')
subplot(2,2,4); plot(D3);
title('Detail D3')
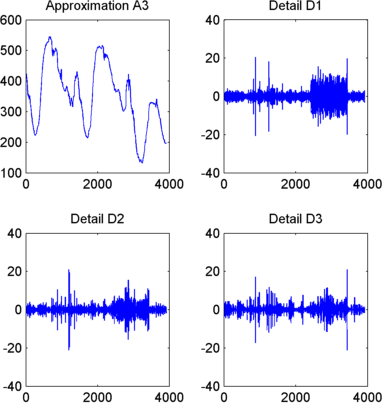
Восстановите исходный сигнал от разложения Уровня 3.
Чтобы восстановить исходный сигнал от структуры разложения вейвлета, ввести
A0 = waverec(C,L,'db1'); err = max(abs(s-A0))
Грубое шумоподавление сигнала.
Используя вейвлеты, чтобы удалить шум из сигнала требует идентификации, какой компонент или компоненты содержат шум и затем восстановление сигнала без тех компонентов.
В этом примере мы отмечаем, что последовательные приближения становятся все меньше и меньше шумными, когда все больше высокочастотной информации отфильтровано из сигнала.
Приближение уровня 3, A3, является довольно чистым как сравнение между ним и исходным сигналом.
Чтобы сравнить приближение с исходным сигналом, ввести
subplot(2,1,1);plot(s);title('Original'); axis off
subplot(2,1,2);plot(A3);title('Level 3 Approximation');
axis off
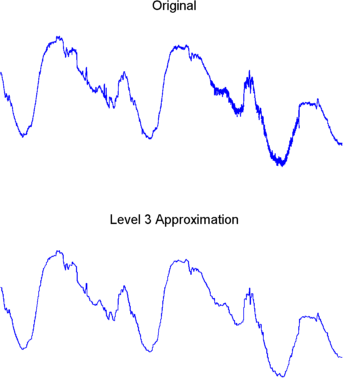
Конечно, в отбрасывании всей высокочастотной информации, мы также потеряли многие самые резкие функции исходного сигнала.
Оптимальное шумоподавление требует, чтобы более тонкий подход вызвал пороговую обработку. Это включает отбрасывание только фрагмента деталей, который превышает определенный предел.
Удалите шум пороговой обработкой.
Давайте посмотрим снова на детали нашего анализа уровня 3.
Отобразить детали D1, D2, и D3Ввод
subplot(3,1,1); plot(D1); title('Detail Level 1'); axis off
subplot(3,1,2); plot(D2); title('Detail Level 2'); axis off
subplot(3,1,3); plot(D3); title('Detail Level 3'); axis off
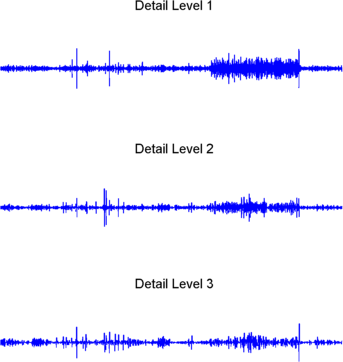
Большая часть шума происходит в последней части сигнала, где детали показывают свое самое большое действие. Что, если мы ограничили силу деталей путем ограничения их максимальных значений? Это оказало бы влияние урезания шума при оставлении деталей незатронутыми через большую часть их длительности. Но существует лучший путь.
Обратите внимание на то, что cD1, cD2, и cD3 только векторы MATLAB®, таким образом, мы могли непосредственно управлять каждым вектором, устанавливая каждый элемент на некоторую часть пикового или среднего значения векторов. Затем мы могли восстановить новые сигналы детали D1, D2, и D3 от пороговых коэффициентов.
К denoise сигнал используйте ddencmp команда, чтобы вычислить параметры по умолчанию и wdencmp команда, чтобы выполнить фактическое шумоподавление, ввести
[thr,sorh,keepapp] = ddencmp('den','wv',s);
clean = wdencmp('gbl',C,L,'db1',3,thr,sorh,keepapp);
Обратите внимание на то, что wdencmp использует результаты разложения (C и L) то, что мы уже вычислили. Мы также указываем, что использовали db1 вейвлет, чтобы выполнить исходный анализ, и мы задаем глобальную опцию пороговой обработки 'gbl'. Смотрите ddencmp и wdencmp на страницах с описанием для получения дополнительной информации об использовании этих команд.
Чтобы отобразить и оригинал и сигналы denoised, ввести
subplot(2,1,1); plot(s(2000:3920)); title('Original')
subplot(2,1,2); plot(clean(2000:3920)); title('denoised')
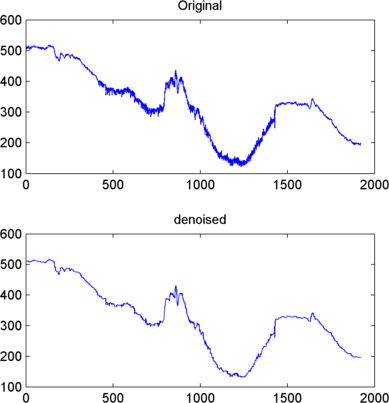
Мы построили здесь только шумную последнюю часть сигнала. Заметьте, как мы удалили шум, не ставя под угрозу резкую деталь исходного сигнала. Это - сила анализа вейвлета.
В то время как использование функций командной строки, чтобы удалить шум из сигнала может быть громоздким, приложение Wavelet Analyzer программного обеспечения включает простую в использовании функцию шумоподавления, которая включает автоматическую пороговую обработку.
Больше информации о процессе шумоподавления может быть найдено в следующих разделах:
Шумоподавление вейвлета и непараметрическая функциональная оценка руководство пользователя Wavelet Toolbox
1D отклонение вейвлета адаптивная пороговая обработка в руководстве пользователя Wavelet Toolbox
В этом разделе мы исследуем тот же электрический сигнал потребления как в предыдущем разделе, но мы используем приложение Wavelet Analyzer, чтобы анализировать и denoise сигнал.
Примечание
Используя приложение Wavelet Analyzer к denoise больше не рекомендуется сигнал. Используйте Wavelet Signal Denoiser вместо этого.
Запустите 1D аналитический инструмент вейвлета.
От подсказки MATLAB ввести waveletAnalyzer.
Wavelet Analyzer появляется.
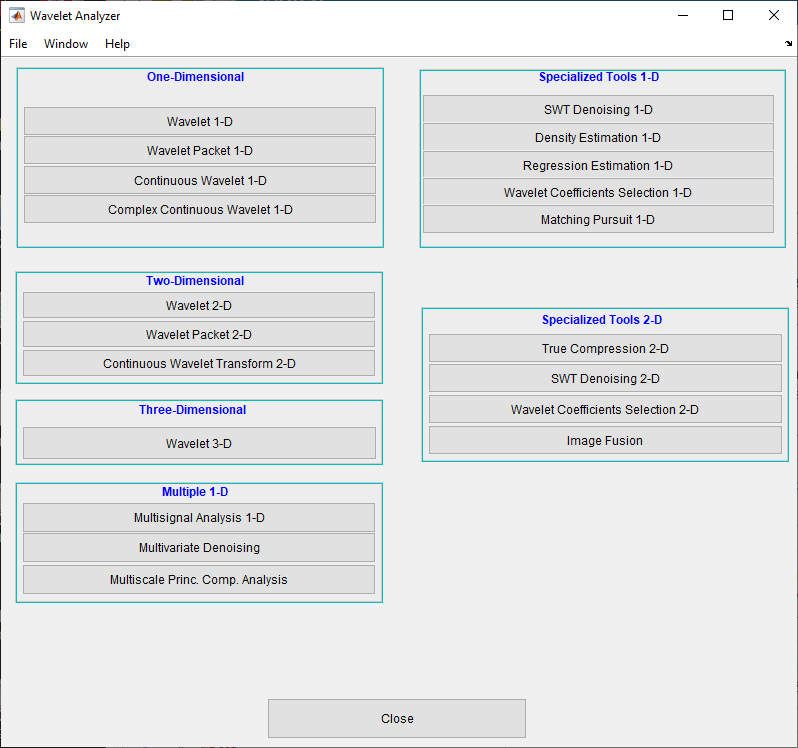
Кликните по пункту меню Wavelet 1-D.
Дискретный аналитический инструмент вейвлета для 1D данных сигнала появляется.
Загрузите сигнал.
В командной строке MATLAB ввести
load leleccum;
leleccum переменная. Нажмите ОК, чтобы импортировать электрический сигнал потребления.Выполните одноуровневое разложение вейвлета.
Чтобы запустить наш анализ, давайте выполним одноуровневое разложение с помощью db1 вейвлет, так же, как мы сделали использование функций командной строки в 1D Анализе Используя Командную строку.
В верхнем правом фрагменте инструмента Wavelet 1-D выберите db1 вейвлет и одноуровневое разложение.
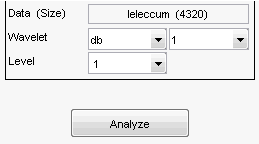
Нажмите кнопку Analyze.
После паузы для расчета инструмент отображает разложение.
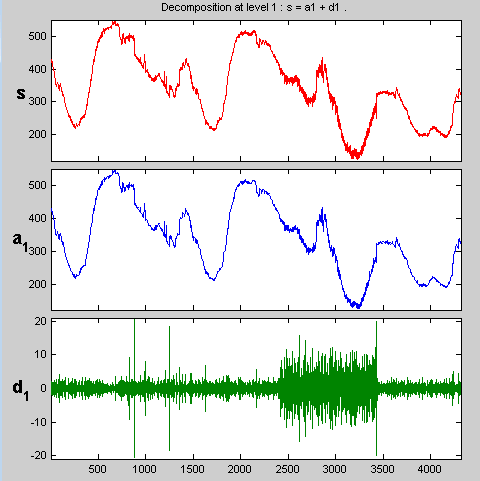
Увеличьте масштаб соответствующей детали.
Одно преимущество использования приложения Wavelet Analyzer состоит в том, что можно увеличить масштаб легко на любой части сигнала и исследовать его более подробно.
Перетащите поле круглой резинки (удержанием левой кнопки мыши) по фрагменту сигнала, который вы хотите увеличить. Здесь, мы выбрали шумную часть исходного сигнала.
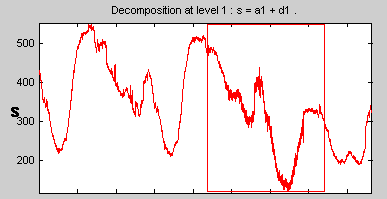
Нажмите кнопку X + (расположенный внизу экрана), чтобы масштабировать горизонтально.
![]()
Инструмент Wavelet 1-D масштабирует все отображенные сигналы.
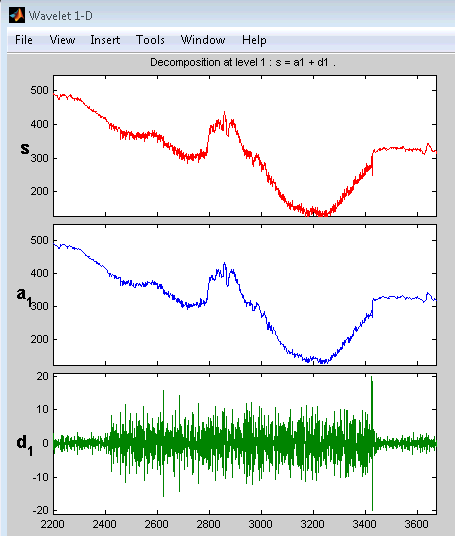
Другие средства управления изменением масштаба делают более или менее, к чему вы ожидали бы их. Кнопка X-, например, уменьшает масштаб горизонтально. Функция истории отслеживает все ваши представления сигнала. Возвратитесь к предыдущему уровню изменения масштаба путем нажатия кнопки стрелки влево.
Выполните многоуровневое разложение.
Снова, мы будем использовать графические инструменты, чтобы эмулировать то, что мы сделали в предыдущем разделе с помощью функций командной строки. Выполнять разложение уровня 3 сигнала с помощью db1 вейвлет:
Выберите 3 из меню Level в верхнем правом углу, и затем нажмите кнопку Analyze снова.

После того, как разложение выполняется, вы будете видеть, что новый анализ появляется в инструменте Wavelet 1-D.
Выбор других взглядов на разложение
Меню Режима отображения (среднее право) позволяет вам выбрать другие взгляды на разложение вейвлета.

Режим отображения по умолчанию называется “Полным Режимом Разложения”. Другие альтернативы включают:
“Отдельный Режим”, который показывает детали и приближения в отдельных столбцах.
“Наложите Режим”, который показывает детали об одном графике, наложенном в различных цветах. Приближения построены так же.
“Древовидный Режим”, который показывает дерево разложения, исходный сигнал и один дополнительный компонент по вашему выбору. Нажмите на дерево разложения, чтобы выбрать компонент сигнала, который требуется просмотреть.
“Покажите и Режим Прокрутки”, который отображает три окна. Первые показы исходный сигнал, наложенный на приближение, вы выбираете. Второе окно показывает деталь, которую вы выбираете. Третье окно показывает коэффициенты вейвлета.
“Покажите, и Режим Прокрутки (Кубический фут в секунду Основы)” очень похож на, “Показывают и Режим Прокрутки” за исключением того, что это отображается, в третьем окне, коэффициенты вейвлета как диаграммы стебель-листья вместо цветных блоков.
Можно изменить режим отображения по умолчанию на базисе на сеанс. Выберите желаемый режим из подменю View> Default Display Mode.
Примечание
Окна Compression и Denoising, открытые от инструмента Wavelet 1-D, наследуют текущий содействующий атрибут визуализации (основы или окрашенные блоки).
В зависимости от которого режима отображения вы выбираете, у вас может быть доступ к дополнительным параметрам отображения через кнопку More Display Options.
Эти опции включают способность подавить отображение различных компонентов и выбрать, отобразить ли исходный сигнал наряду с деталями и приближениями.
Удалите шум из сигнала.
Функции приложения Wavelet Analyzer опция шумоподавления с предопределенной стратегией пороговой обработки. Это делает очень легким удалить шум из сигнала.
Примечание
Опция шумоподавления больше не рекомендуется. Используйте Wavelet Signal Denoiser вместо этого.
Поднимите инструмент шумоподавления: нажмите denoise кнопку, расположенную в среднем праве на окно, под кнопкой Analyze.
Окно Wavelet 1-D Denoising появляется.
В то время как много опций доступны для подстройки алгоритма шумоподавления, мы примем значения по умолчанию мягкой фиксированной пороговой обработки формы и немасштабированного белого шума. Unscaled white noise опция соответствует установке мультипликативного порогового входного параметра SCAL из wden к 'one'. Выбор Scaled white noise соответствует 'sln', и Non-white noise соответствует 'mln'. Для получения дополнительной информации смотрите wden.
Продолжите путем нажатия denoise кнопки.
Сигнал denoised кажется наложенным на оригинале. Инструмент также строит коэффициенты вейвлета обоих сигналов. Исходные коэффициенты детали появляются на левой стороне отображения. Для того, чтобы ко времени выравнивают уровни разложения через все шкалы, коэффициенты вейвлета реплицированы в каждую шкалу с учетом недостающих моментов времени. Поэтому, когда шкала становится более грубой, коэффициенты принимают подобный лестнице внешний вид.
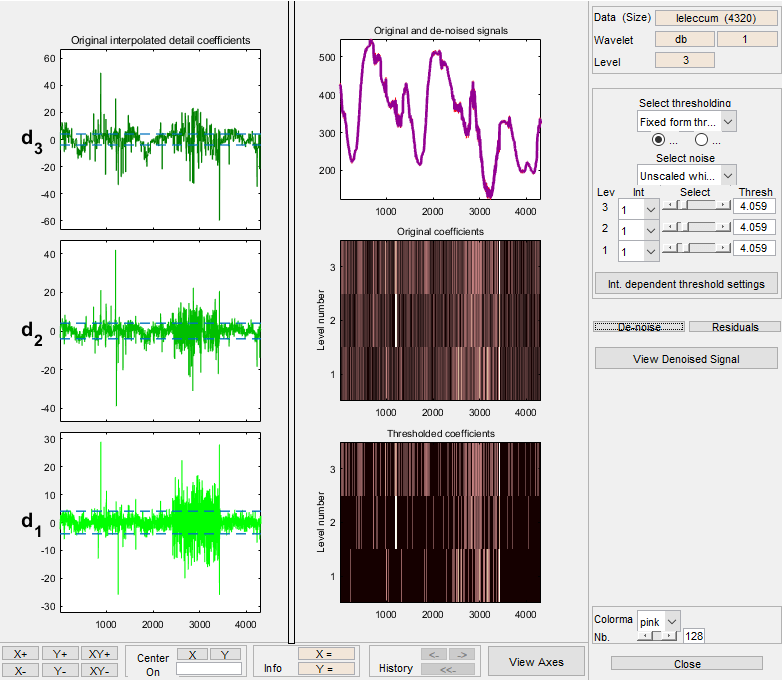
Увеличьте масштаб графика оригинала и сигналов denoised для более внимательного рассмотрения.
Перетащите поле круглой резинки вокруг подходящей области, и затем нажмите кнопку XY +.
denoise окно увеличивает ваше представление. По умолчанию исходный сигнал отображают красным и сигналом denoised желтого цвета.
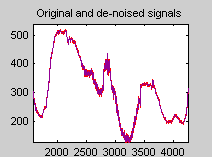
Отклоните окно Wavelet 1-D Denoising: нажмите кнопку Close.
Вы не можете иметь denoise и окон Compression, открытых одновременно, поэтому закрыть окно Wavelet 1-D Denoising, чтобы продолжиться. Когда диалоговое окно Update Synthesized Signal появляется, нажмите No. If, вы нажимаете кнопку Да, Синтезируемый Сигнал затем доступен в главном окне Wavelet 1-D.
Совершенствуйте анализ.
Графические инструменты дают возможность совершенствовать анализ любое время, вы хотите. До сих пор мы посмотрели на анализ уровня 3 с помощью db1. Давайте совершенствуем наш анализ электрического сигнала потребления использование db3 вейвлет на уровне 5.
Выберите 5 из меню Level в верхнем правом углу и выберите db3 в меню Wavelet. Нажмите кнопку Analyze.
Сожмите сигнал.
Инструменты графического интерфейса показывают опцию сжатия с автоматической или ручной пороговой обработкой.

Поднимите окно Compression: нажмите кнопку Compress, расположенную в среднем праве на окно, под кнопкой Analyze.
Окно Compression появляется.
В то время как у вас всегда есть опция выбора пороговой обработкой уровня, здесь мы используем в своих интересах глобальную функцию пороговой обработки быстрого и легкого сжатия.
Примечание
Если вы хотите экспериментировать с ручной пороговой обработкой, выбрать опцией пороговой обработки Уровня в меню, расположенном в правом верхнем из окна Wavelet 1-D Compression. Ползунки, расположенные ниже этого меню затем, управляют зависимыми уровнем порогами, обозначенными желтыми пунктирными линиями, запускающимися горизонтально через графики слева от окна. Желтые пунктирные линии могут также быть перетащены непосредственно с помощью левой кнопки мыши.
Нажмите кнопку Compress, расположенную в центральном праве.
После паузы для расчета электрический сигнал потребления вновь отображен в красном со сжатой версией, наложенной в желтом. Ниже, мы увеличили масштаб, чтобы получить более внимательное рассмотрение в шумной части сигнала.
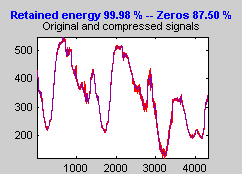
Вы видите, что процесс сжатия удалил большую часть шума, но сохранил 99,99% энергии сигнала.
От инструмента Wavelet 1-D Compression нажмите кнопку Residuals. Окно More on Residuals for Wavelet 1-D Compression появляется.
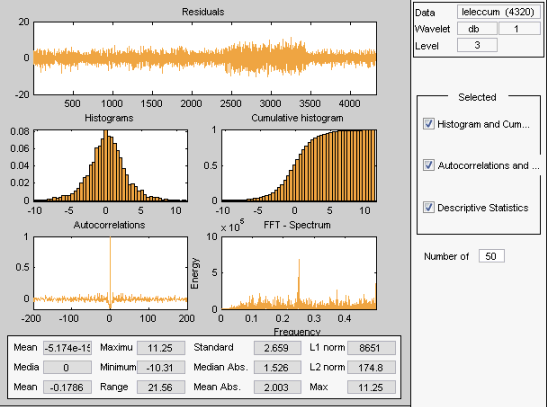
Отображенные статистические данные включают меры тенденции (среднее значение, режим, медиана) и дисперсия (область значений, стандартное отклонение). Кроме того, инструмент предоставляет схемы плотности распределения (гистограммы и совокупные гистограммы), а также схемы timeseries: автокорреляционная функция и спектр. Та же функция существует для инструмента Wavelet 1-D Denoising.
Отклоните окно Wavelet 1-D Compression: нажмите кнопку Close. Когда диалоговое окно Update Synthesized Signal появится, нажмите No.
Покажите статистику.
Можно просмотреть множество статистических данных о сигнале и его компонентах.
От инструмента Wavelet 1-D нажмите кнопку Statistics.

Окно Wavelet 1-D Statistics кажется отображающимся статистикой по умолчанию по исходному сигналу.
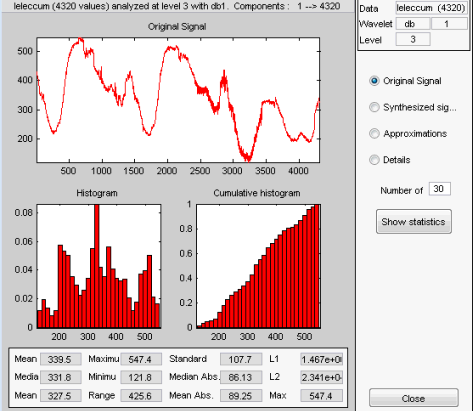
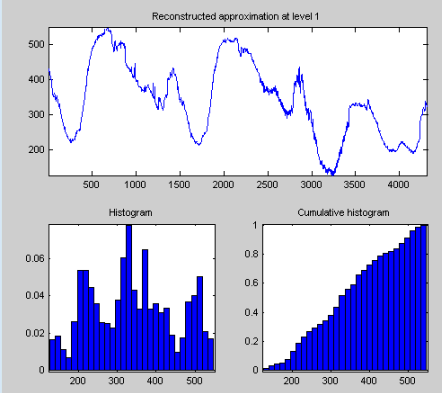
Выберите синтезируемый компонент сигнала или сигнала, статистику которого вы хотите исследовать. Нажмите кнопку подходящего варианта, и затем нажмите кнопку Show Statistics. Здесь, мы приняли решение исследовать синтезируемый сигнал с помощью 100 интервалов вместо 30, который является значением по умолчанию:
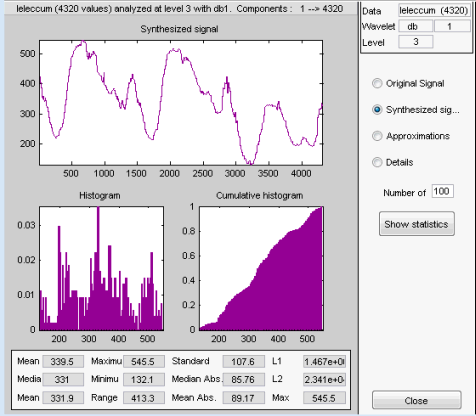
Отображенные статистические данные включают меры тенденции (среднее значение, режим, медиана) и дисперсия (область значений, стандартное отклонение).
Кроме того, инструмент предоставляет схемы плотности распределения (гистограммы и совокупные гистограммы). Можно построить эти гистограммы отдельно с помощью кнопки Histograms из окна Wavelets 1-D.
Кликните по переключателю Approximation. Меню появляется, из которого вы выбираете уровень приближения, которое вы хотите исследовать.
Выберите Level 1 и снова нажмите кнопку Show Statistics. Статистические данные появляются для приближения уровня 1.
Вейвлет 1D инструмент графического интерфейса позволяет вам импортировать информацию из и экспортировать информацию в диск и рабочее пространство MATLAB.
Можно сохранить синтезируемые сигналы, коэффициенты и разложения от инструмента Wavelet 1-D до диска, где информацией можно управлять и позже повторно импортировать в графический инструмент.
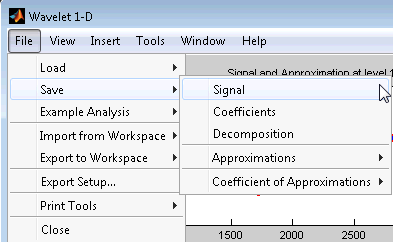
Сохранение Синтезируемых Сигналов. Можно обработать сигнал в инструменте Wavelet 1-D и затем сохранить обработанный сигнал в MAT-файл (с дополнительным mat или другой).
Например, загрузите анализ в качестве примера: Файл> Анализ В качестве примера> Базовые сигналы> с db3 на уровне 5 → Сумма синусов, и выполняет операцию сжатия или шумоподавления на исходном сигнале. Когда вы закрываете окно Denoising или Compression, обновляете синтезируемый сигнал путем нажимания кнопку Да в диалоговом окне.
Затем от инструмента Wavelet 1-D выберите пункт меню File> Save> Signal.
Диалоговое окно кажется позволяющим вам, чтобы выбрать папку и имя файла для MAT-файла. В данном примере выберите имя synthsig.
Чтобы загрузить сигнал в вашу рабочую область, просто введите
load synthsig;
Когда синтезируемый сигнал получен с помощью любого метода задания порога кроме глобального, сохраненная структура
whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
synthsig | 1x1000 | 8000 | double массив |
thrParams | 1x5 | 580 | cell array |
wname | 1x3 | 6 | char array |
Синтезируемый сигнал дан переменной synthsig. Кроме того, параметры процесса шумоподавления или сжатия даны именем вейвлета (wname) и зависимые пороги уровня содержатся в thrParams переменная, которая является массивом ячеек длины 5 (то же самое как уровень разложения).
Для i от 1 до 5, thrParams{i} содержит нижние и верхние границы интервала пороговой обработки и порогового значения (поскольку зависимые пороги интервала позволены, смотрите 1D Адаптивную Пороговую обработку Коэффициентов Вейвлета).
Например, для уровня 1,
thrParams{1}
ans =
1.0e+03 *
0.0010 1.0000 0.0014
Когда синтезируемый сигнал получен с помощью глобального метода задания порога, сохраненная структура
| Имя | Размер | Байты | Класс |
|---|---|---|---|
synthsig | 1x1000 | 8000 | double array |
valTHR | 1x1 | 8 | double array |
wname | 1x3 | 6 | char array |
где переменная valTHR содержит глобальный порог:
valTHR
valTHR =
1.2922
Сохранение Дискретных Коэффициентов Преобразования Вейвлета. Инструмент Wavelet 1-D позволяет вам сохранить коэффициенты дискретного вейвлета преобразовывает (DWT) к диску. Тулбокс создает MAT-файл в текущей папке с именем, которое вы выбираете.
Чтобы избавить коэффициенты DWT от существующего анализа, используйте пункт меню File> Save> Coefficients.
Диалоговое окно появляется, который позволяет вам задать папку и имя файла для хранения коэффициентов.
Рассмотрите анализ в качестве примера:
Файл> Анализ В качестве примера> Базовые сигналы> с db1 на уровне 5 → Канторова кривая.
После сохранения коэффициентов вейвлета к файлу cantor.mat, загрузите переменные в рабочей области:
load cantor whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
coefs | 1x2190 | 17520 | double array |
longs | 1x7 | 56 | double array |
thrParams | 0x0 | 0 | double array |
wname | 1x3 | 6 | char array |
Переменный coefs содержит дискретные коэффициенты вейвлета. Более точно, в вышеупомянутом примере coefs 1 2190 вектор из конкатенированных коэффициентов и longs вектор, дающий длины каждого компонента coefs.
Переменный wname содержит имя вейвлета и thrParams пусто, поскольку синтезируемый сигнал не существует.
Сохранение Разложений. Инструмент Wavelet 1-D позволяет вам сохранить целый набор данных от дискретного анализа вейвлета до диска. Тулбокс создает MAT-файл в текущей папке с именем, которое вы выбираете, сопровождаемый дополнительным wa1 (1D анализ вейвлета).
Откройте инструмент Wavelet 1-D и загрузите анализ в качестве примера:
Файл> Анализ В качестве примера> Базовые сигналы> с db3 на уровне 5 → Сумма синусов
Чтобы сохранить данные от этого анализа, используйте пункт меню File> Save> Decomposition.
Диалоговое окно появляется, который позволяет вам задать папку и имя файла для того, чтобы хранить данные о разложении. Введите имя wdecex1d.
После сохранения данных о разложении к файлу wdecex1d.wa1, загрузите переменные в свою рабочую область:
load wdecex1d.wa1 -mat whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
coefs | 1x1023 | 8184 | double array |
data_name | 1x6 | 12 | char array |
longs | 1x7 | 56 | double array |
thrParams | 0x0 | 0 | double array |
wave_name | 1x3 | 6 | char array |
Примечание
Сохраните опции, также доступны при выполнении шумоподавления или сжатия в инструменте Wavelet 1-D. В окне Wavelet 1-D Denoising можно сохранить сигнал denoised и разложение. То же самое сохраняется для окна Wavelet 1-D Compression. Таким образом, можно сохранить много различных испытаний из окон Denoising и Compression, не возвращаясь к основному окну Wavelet 1-D во время процесса подстройки.
Примечание
При сохранении синтезируемого сигнала, разложения или коэффициентов к MAT-файлу, mat расширение файла не необходимо. Можно сохранить приближения индивидуально для каждого уровня или сохранить их целиком.
Инструмент Wavelet 1-D позволяет вам экспортировать свой 1D анализ вейвлета в рабочее пространство MATLAB во многих форматах.
Например, загрузите анализ в качестве примера для freqbrk сигнал.
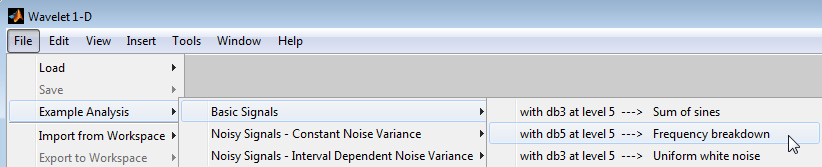
После вейвлета 1D аналитические загрузки выберите File —> Export to Workspace.
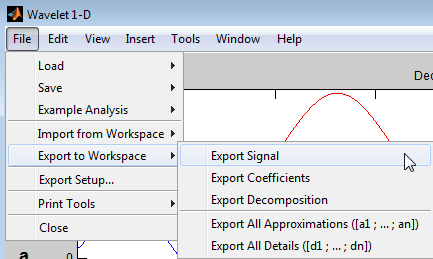
У вас есть опция к
Export Signal — Эта опция экспортирует синтезируемый сигнальный вектор.
Export Coefficients — Эта опция экспортирует вектор из вейвлета и масштабных коэффициентов, бухгалтерский вектор и вейвлет анализа в массиве структур. Вейвлет и масштабный коэффициент и бухгалтерские векторы идентичны выходу wavedec.
Export Decomposition — Эта опция идентична Export Coefficients за исключением того, что это также содержит имя анализируемого сигнала.
Export All Approximations — Эта опция экспортирует L-by-N матрицу, где L является значением Level, и N является длиной входного сигнала. Каждая строка матрицы является проекцией на пробел приближения на соответствующем уровне. Например, первая строка матрицы является проекцией на пробел приближения на уровне 1.
Export All Details — Эта опция экспортирует L-by-N матрицу, где L является значением Level, и N является длиной входного сигнала. Каждая строка матрицы является проекцией на деталь (вейвлет) пробел на соответствующем уровне. Например, первая строка матрицы является проекцией на пробел детали на уровне 1.
Можно загрузить сигналы, коэффициенты или разложения в приложение Wavelet Analyzer. Информация, которую вы загружаете, возможно, ранее экспортировалась из приложения и затем управлялась в рабочей области, или это, возможно, была информация, которую вы сгенерировали первоначально из командной строки.
Или в случае, необходимо наблюдать строгие форматы файлов и структуры данных, используемые инструментом Wavelet 1-D, или иначе в ошибки закончатся, когда вы попытаетесь загрузить информацию.
Загрузка Сигналов. Чтобы загрузить сигнал, вы создали в своем рабочем пространстве MATLAB в инструмент Wavelet 1-D, сохраните сигнал в MAT-файле (с дополнительным mat или другой).
Например, предположите, что вы спроектировали сигнал под названием warma и хочу анализировать его в инструменте Wavelet 1-D.
save warma warma
Переменная рабочей области warma должна быть вектором.
sizwarma = size(warma)
sizwarma =
1 1000
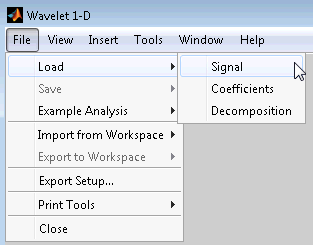
Чтобы загрузить этот сигнал в инструмент Wavelet 1-D, используйте пункт меню File> Load> Signal.
Диалоговое окно появляется, который позволяет вам выбрать соответствующий MAT-файл, чтобы загрузиться.
Примечание
Первая 1D переменная, с которой сталкиваются в файле, рассматривается сигналом. Переменные смотрятся в алфавитном порядке.
Загрузка Дискретных Коэффициентов Преобразования Вейвлета. Чтобы загрузить дискретный вейвлет преобразовывают коэффициенты в инструмент Wavelet 1-D, необходимо сначала сохранить соответствующие данные в MAT-файле, который должен содержать, по крайней мере, эти две переменные coefs и longs.
Переменный coefs должен быть вектор из коэффициентов DWT (конкатенированный для различных уровней), и переменная longs вектор, задающий длину каждого компонента coefs, а также длина исходного сигнала.
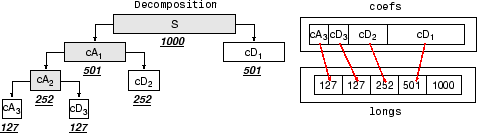
После построения или редактирования соответствующих данных в вашей рабочей области, ввести
save myfile coefs longs
Используйте пункт меню File> Load> Coefficients от инструмента Wavelet 1-D, чтобы загрузить данные в графический инструмент.
Диалоговое окно появляется, позволяя вам выбрать папку и файл, в котором находятся ваши данные.
Загрузка Разложений. Чтобы загрузить дискретный вейвлет преобразовывают данные о разложении в Вейвлет 1D графический интерфейс, необходимо сначала сохранить соответствующие данные в MAT-файле (с дополнительным wa1 или другой).
MAT-файл содержит следующие переменные.
| Переменная | Состояние | Описание |
|---|---|---|
coefs | Необходимый | Вектор из конкатенированных коэффициентов DWT |
longs | Необходимый | Продолжительности определения вектора компонентов |
wave_name | Необходимый | Имя определения вектора символов вейвлета используется для разложения (например, |
data_name | Дополнительный | Имя определения вектора символов разложения |
После построения или редактирования соответствующих данных в вашей рабочей области, ввести
save myfile coefs longs wave_name
Используйте пункт меню File> Load> Decomposition от инструмента Wavelet 1-D, чтобы загрузить данные о разложении в графический инструмент.
Диалоговое окно появляется, позволяя вам выбрать папку и файл, в котором находятся ваши данные.
Примечание
При загрузке сигнала, разложения или коэффициентов из MAT-файла, расширение этого файла свободно. mat расширение не необходимо.
Wavelet Signal Denoiser | wdenoise