Выполнить топологический вид направленного ациклического графа
order = graphtopoorder(G)
G | N-по-N разреженная матрица, которая представляет направленный ациклический граф. Ненулевые записи в матрице G указывают на наличие ребра. |
Совет
Вводные сведения о функциях теории графов см. в разделе Функции теории графов.
order = graphtopoorder(G)u и узел назначения v, если и только если u появляется перед v в векторе order. G - разреженная матрица N-на-N, представляющая направленный ациклический граф (DAG). Ненулевые записи в матрице G указывают на наличие ребра.
Создайте и просмотрите направленный ациклический граф (DAG) с шестью узлами и восемью ребрами.
DG = sparse([6 6 6 2 2 3 5 1],[2 5 1 3 4 5 1 4],true,6,6) DG = (5,1) 1 (6,1) 1 (6,2) 1 (2,3) 1 (1,4) 1 (2,4) 1 (3,5) 1 (6,5) 1 view(biograph(DG))
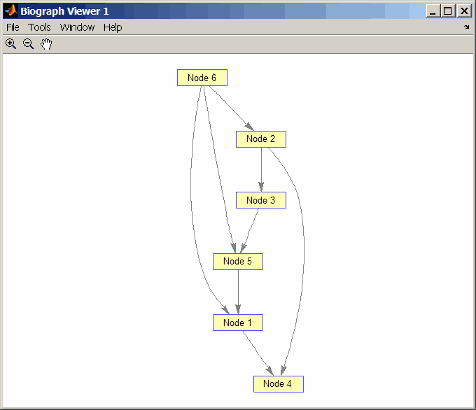
Найдите топологический порядок группы обеспечения доступности баз данных.
order = graphtopoorder(DG)
order =
6 2 3 5 1 4
Переставьте узлы таким образом, чтобы они появлялись упорядоченными в отображении графика.
DG = DG(order,order) DG = (1,2) 1 (2,3) 1 (1,4) 1 (3,4) 1 (1,5) 1 (4,5) 1 (2,6) 1 (5,6) 1 view(biograph(DG))
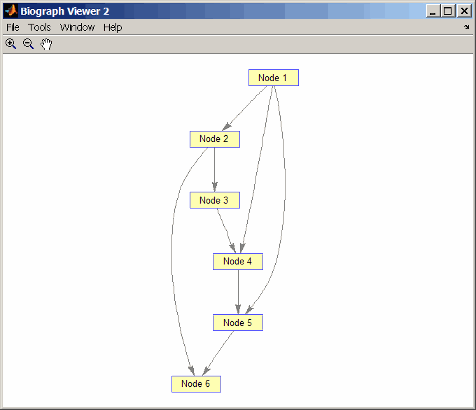
[1] Сиек, Дж. Г., Ли, L-Q, и Люмсдейн, А. (2002). Руководство пользователя и справочное руководство библиотеки Boost Graph (Upper Saddle River, NJ: Pearson Education).
graphallshortestpaths | graphconncomp | graphisdag | graphisomorphism | graphisspantree | graphmaxflow | graphminspantree | graphpred2path | graphshortestpath | graphtraverse | topoorder