Декодирование кода Рида-Соломона для восстановления двоичных векторных данных
Панель инструментов связи/Обнаружение и исправление ошибок/Блок
Блок RS-декодера двоичного выхода восстанавливает вектор двоичного сообщения из вектора двоичного кодового слова Рида-Соломона. Для правильного декодирования значения параметров в этом блоке должны совпадать со значениями параметров в соответствующем блоке RS-кодера двоичного ввода.
Символами для кода являются двоичные последовательности длиной М, соответствующие элементам поля Галуа GF (2M). Первый бит в каждом символе является самым значительным битом .
На этом рисунке показана длина слова ввода-вывода декодера для длины кодового слова N = 7 и длины слова сообщения K = 2. Поскольку N = 2M-1, когда N = 7, длина символа M = 3.
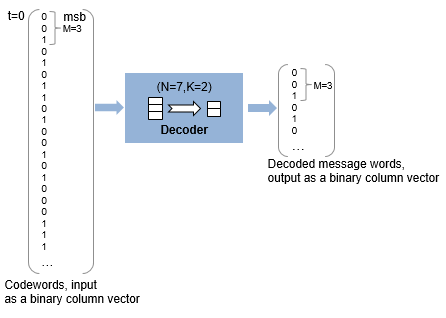
Каждое входное кодовое слово является двоичным вектором длиной 21, который представляет 7 трёхбитовых целых чисел. Каждое соответствующее выходное слово сообщения является двоичным вектором длиной 6, который представляет 2 трёхбитовых целых числа. Дополнительные сведения см. в разделе Длина входного и выходного сигнала в блоках RS.
Этот значок показывает все порты, включая дополнительные: ![]()
In - Кодовое слово Рида - СоломонаКодовое слово Рида - Соломона в битах, указанное как (NC × (N - K + S - P) × M) -by-1 двоичный вектор-столбец. NC - количество кодовых слов, N - длина кодового слова N (символы), K - длина сообщения K (символы), S - длина укороченного сообщения S (символы), P - количество проколов на кодовое слово, и M - количество битов на символ.
Дополнительные сведения см. в разделе Длина входного и выходного сигнала в блоках RS.
Типы данных: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean | ufix(1)
Era - Вектор стиранияВектор стирания в символах, заданный как (NC × (N - K + S - P)) -by-1 двоичный вектор-столбец. NC - количество кодовых слов, N - длина кодового слова N (символы), K - длина сообщения K (символы), S - длина укороченного сообщения S (символы), P - количество проколов на кодовое слово, и M - количество битов на символ.
Значения стирания 1 соответствуют стертым битам в одной позиции в кодовом слове. Значения 0 соответствуют битам, которые не стерты. Дополнительные сведения см. в разделе Прокалывание и стирание.
Чтобы включить этот порт, выберите Enable erasures input port.
Типы данных: double | Boolean
Out - Декодированное сообщениеДекодированное сообщение в битах, возвращаемое как одно из следующих:
При отсутствии укорочения сообщения двоичный вектор столбца (NC × K × M) -by-1.
При укорочении сообщения двоичный вектор столбца (NC × S × M) -by-1.
NC - количество слов сообщения, K - длина сообщения K (символы), M - количество битов на символ, S - длина укороченного сообщения S (символы).
Примечание
Количество декодированных слов сообщения равно количеству кодовых слов.
Дополнительные сведения см. в разделе Длина входного и выходного сигнала в блоках RS.
Типы данных: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean | ufix(1)
Err - Ошибки декодированияОшибки декодирования символов, возвращаемые как целочисленный вектор с элементами ЧПУ, где ЧПУ - количество кодовых слов. Этот порт указывает количество символьных ошибок, обнаруженных во время декодирования каждого кодового слова. Отрицательное целое число указывает, что блок обнаружил больше ошибок, чем мог бы исправить с помощью указанной схемы кодирования.
Примечание
Код Рида-Соломона (N, K) может исправлять до floor((N-K)/2) символьные ошибки (не битовые ошибки) в каждом кодовом слове. Когда принятое кодовое слово содержит более (N-K )/2 символьных ошибок, происходит сбой декодирования .
Чтобы включить этот порт, выберите Output number of corrected symbol errors.
Типы данных: double
Дополнительные сведения см. в разделе Поддерживаемые типы данных.
Codeword length N (symbols) - Длина кодового слова7 (по умолчанию) | целое числоДлина кодового слова в символах, заданная как целое число.
Дополнительные сведения см. в разделе Ограничения длины N M и кодового слова и длины входного и выходного сигнала в блоках RS.
Message length K (symbols) - Длина слова сообщения3 (по умолчанию) | целое числоДлина слова сообщения в символах, заданная как целое число в диапазоне [1, N-2], где N - длина кодового слова.
Shortened message length S (symbols) - Сокращенная длина слова сообщения3 (по умолчанию) | целое числоУкороченная длина слова сообщения в символах, заданная как целое число, так что S ≤ K. Когда укороченная длина сообщения S (символы) < длина сообщения K (символы), код Рида-Соломона укорачивается.
Значения N и K по-прежнему задаются для полноразмерного (N, K) кода, но декодирование сокращается до кода (N-K + S, S).
Чтобы включить этот параметр, выберите Указать укороченную длину сообщения.
Generator polynomial - Полином генератораrsgenpoly(7, 3, [], [], 'double') (дефолт) | многочленный вектор характера | вектор строки двоичных знаков | набор из двух предметов вектор ряда ГалуаГенераторный многочлен со значениями от 0 до 2M-1 в порядке убывания мощности, заданными как одно из следующих:
Вектор многочлена. Дополнительные сведения см. в разделе Символьное представление многочленов.
Целочисленный вектор строки, представляющий коэффициенты генераторного многочлена в порядке степени убывания.
Целочисленный вектор строки Галуа, представляющий коэффициенты генераторного многочлена в порядке степени убывания.
Каждый коэффициент является элементом поля Галуа, определяемым примитивным многочленом. Дополнительные сведения см. в разделе Задание полинома генератора.
Пример: [1 3 1 2 3], что эквивалентно rsgenpoly(7,3)
Чтобы включить этот параметр, выберите Задать полином генератора (Specify generator polynomial).
Primitive polynomial - примитивный многочлен'X^3 + X + 1' (по умолчанию) | вектор многочлена | двоичный вектор строкиПримитивный многочлен в порядке степени убывания. Этот многочлен имеет порядок M и определяет конечное поле Галуа GF (2M), соответствующее целым числам, которые образуют слова сообщения и кодовые слова. Укажите примитивный многочлен как один из следующих:
Вектор многочлена. Дополнительные сведения см. в разделе Символьное представление многочленов.
Двоичный вектор строки, представляющий коэффициенты полинома генератора.
Дополнительные сведения см. в разделе Ограничения длины M и кодового слова N.
Пример: 'X^3 + X + 1', который является примитивным многочленом, используемым для (7,3) кода, de2bi(primpoly(3,'nodisplay'),'left-msb')
Чтобы включить этот параметр, выберите Задать примитивный полином.
Puncture vector - Вектор прокола[ones(2,1); zeros(2,1)] (по умолчанию) | двоичный вектор столбцаВектор прокола, заданный как вектор двоичного столбца (N-K) -by-1. Индексы элементов с1s представляют индексы символов данных, которые проходят через блок без изменений. Индексы элементов с 0s представляют индексы символов данных, которые проколоты или удалены из потока данных. Дополнительные сведения см. в разделе Прокалывание и стирание.
Чтобы включить этот параметр, выберите Пунктированный код.
Enable erasures input port - Включить входной порт стиранияПри установке этого флажка включается порт стирания Era. Дополнительные сведения см. в разделе Прокалывание и стирание.
Output number of corrected symbol errors - Включить порт для вывода количества исправленных ошибок символовУстановка этого флажка включает дополнительный выходной порт Err, который указывает количество ошибок символов, исправленных блоком во входном кодовом слове.
Output data type - Тип вывода блокаSame as input (по умолчанию) | boolean | doubleТип вывода блока, указанный как Same as input, boolean, или double.
Код Рида-Соломона имеет длину слова сообщения, K, или длину укороченного слова сообщения, S. Длина кодового слова равна N - K + S - P, где N - полная длина кодового слова, а P - количество проколов на кодовое слово. Когда нет укорочения сообщения, выражение длины кодового слова уменьшается до N - P, поскольку K = S. Если декодер обрабатывает несколько кодовых слов в кадре, то один и тот же шаблон прокола сохраняется для всех кодовых слов.
В этой таблице представлены выражения длины входного и выходного сигналов для кодера Рида-Соломона и декодера.
Обозначение y = NC × x обозначает, что y является целым числом, кратным x.
| Длина входного, выходного и выходного векторов | ||
|---|---|---|
| Кодер блоков RS | Сокращение сообщений не используется | Используется сокращение сообщений |
|
Кодер RS с двоичным входом |
Длина входа (биты): NC × K × M Длина выходного сигнала (биты): NC × (N-P) × M |
Длина входа (биты): NC × S × M Длина выходного сигнала (биты): NC × (N-K + S-P) × M |
|
Декодер RS с двоичным выходом |
Длина входа (биты): NC × (N-P) × M Длина стирания (символы): NC × (N-P) Длина выходного сигнала (биты): NC × K × M |
Длина входа (биты): NC × (N-K + S-P) × M Длина стирания (символы): NC × (N-K + S-P) Длина выходного сигнала (биты): NC × S × M |
N - длина кодового слова.
K - длина слова сообщения.
S - укороченная длина слова сообщения.
NC - количество кодовых слов (и слов сообщения).
P - число проколов на кодовое слово и равно числу нулей в векторе прокола.
M - степень примитивного многочлена. Каждая группа из М битов представляет целое число между 0 и 2M–1 которая принадлежит конечному полю Галуа GF(2M).
Дополнительные сведения о представлении данных для кодов Рида-Соломона см. в разделе Целочисленный формат (только для Рида-Соломона).
Также см. Ограничения на длину M и кодового слова N.
Если не выбран параметр Указать примитивный многочлен, допустимые значения длины кодового слова N составляют от 7 до 65535. В этом случае блок использует примитивный многочлен степени по умолчанию M = ceil(log2(N+1)). Можно отобразить полином примитива по умолчанию, выполнив команду primpoly(ceil(log2(N+1))).
Если выбран параметр Задать примитивный многочлен (Specify primitive polynomial), допустимые значения степени примитивного многочлена M составляют от 3 до 16. Допустимые значения для N в этом случае составляют от 7 до 2M-1. Выбор параметра «Указать примитивный многочлен» позволяет задать примитивный многочлен, определяющий конечное поле GF (2M), которое соответствует значениям, образующим слова сообщения и кодовые слова.
Выберите Задать полином генератора (Specify generator polynomial), чтобы включить параметр Полином генератора (Generator polynomial) для задания полинома генератора кода Рида-Соломона. Введите целочисленный вектор строки со значениями элементов от 0 до 2M-1. Вектор представляет многочлен в порядке убывания степеней, коэффициенты которого являются элементами GF (2M), представленными в целочисленном формате. Дополнительные сведения о целочисленном и двоичном форматах см. в разделе Целочисленный формат (только для Рида-Соломона). Генераторный многочлен должен быть равен многочлену с такой факторизованной формой:
g (x) = (x + αb) (x + αb + 1) (x + αb + 2)... (x + αb + N-K-1)
α - примитивный элемент поля Галуа, над которым определено входное сообщение, а b - целое число.
Если не выбран параметр Задать полином генератора (Specify generator polynomial), блок использует для кодирования Рида-Соломона полином генератора по умолчанию, соответствующий b = 1. Можно отобразить полином генератора по умолчанию, выполнив командуrsgenpoly.
Если используется примитивный многочлен по умолчанию (не выбран параметр «Указать примитивный многочлен»), используется полином генератора по умолчанию rsgenpoly(N,K), где N = 2M-1.
Если не используется примитивный многочлен по умолчанию (выбран параметр Указать примитивный многочлен) и указывается примитивный многочлен как poly, генераторный многочлен rsgenpoly(N,K,poly).
Примечание
Степень полинома генератора равна N − K, где N - длина кодового слова, а K - длина слова сообщения.
1s и 0s имеют совершенно противоположные значения для векторов прокола и стирания.
В векторе прокола,
1 означает, что символ данных проходит через блок без изменений.
0 означает, что символ данных должен быть проколот или удален из потока данных.
В векторе стирания
1 означает, что символ данных должен быть заменен символом стирания.
0 означает, что символ данных проходит через блок без изменений.
Эти условные обозначения применимы как к кодеру, так и к декодеру. Дополнительные сведения см. в разделах Укорочение, прокалывание и стирание.
| Порт | Поддерживаемые типы данных |
|---|---|
| В |
|
| Из |
|
| Эра |
|
| Допустить ошибку |
|
Этот блок использует алгоритм декодирования Берлекампа-Мэсси. Сведения об этом алгоритме см. в разделе Алгоритмы декодирования только ошибок BCH и RS.
[1] Уикер, Стивен Б. Системы управления ошибками для цифровой связи и хранения. Река Верхнее Седло, Нью-Джерси: Прентис Холл, 1995.
[2] Берлекамп, Элвин Р. Алгебраическая теория кодирования. Нью-Йорк: Макгроу-Хилл, 1968.
[3] Кларк, Джордж К. младший и J. Затвор Каин. Кодирование с исправлением ошибок для цифровой связи. Нью-Йорк: Пленум Пресс, 1981.
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.