Улучшение частоты ошибок с помощью перемежения блоков в MATLAB
Улучшение частоты ошибок с помощью перемежения блоков в Simulink
Блочный перемежитель принимает набор символов и перегруппирует их, не повторяя и не пропуская ни один из символов в наборе. Количество символов в каждом наборе фиксировано для данного перемежителя. Работа перемежителя над набором символов не зависит от его работы над всеми другими наборами символов.
Перемежитель переставляет символы в соответствии с отображением. Соответствующий обращенный перемежитель использует обратное отображение для восстановления исходной последовательности символов. Перемежение и обратное перемежение могут быть полезны для уменьшения ошибок, вызванных пакетными ошибками в системе связи.
Каждая функция перемежителя имеет соответствующую функцию обращенного перемежителя. При типичном использовании пар перемежитель/обращенный перемежитель входы обращенного перемежителя совпадают с входами перемежителя, за исключением переупорядочиваемых данных.
Блочный перемежитель принимает набор символов и перегруппирует их, не повторяя и не пропуская ни один из символов в наборе. Количество символов в каждом наборе фиксировано для данного перемежителя.
Набор перемежителей блоков в этой панели инструментов включает в себя общий перемежитель блоков, а также несколько специальных случаев. Каждая специальная функция перемежителя использует тот же вычислительный код, который использует общая блочная функция перемежителя, но обеспечивает синтаксис, который более подходит для специального случая. Функции перемежителя описаны ниже.
| Тип перемежителя | Функция перемежителя | Описание |
|---|---|---|
| Общий блочный перемежитель | intrlv | Использует таблицу перестановок, явно заданную в качестве входного аргумента. |
| Алгебраический перемежитель | algintrlv | Выводит таблицу перестановок алгебраически, используя метод Такешиты-Костелло или Уэлча-Костаса. Эти способы описаны в [4]. |
| Перемежитель спирального сканирования | helscanintrlv | Заполняет матрицу строками данных, а затем отправляет содержимое матрицы на выход по спирали. |
| Матричный перемежитель | matintrlv | Заполняет матрицу элементами данных по строкам, а затем отправляет содержимое матрицы в выходной столбец по столбцам. |
| Случайный перемежитель | randintrlv | Случайный выбор таблицы перестановок с использованием вводимого начального состояния. |
Типы перемежителей блоков. Набор блочных перемежителей в этой библиотеке включает в себя общую пару перемежитель/обращенный перемежитель, а также несколько специальных случаев. Каждый блок специального случая использует тот же вычислительный код, что и его более общий аналог, но обеспечивает интерфейс, который более подходит для специального случая.
Блок перемежителя матриц выполняет перемежение блоков, заполняя матрицу входными символами по строкам и затем посылая содержимое матрицы в столбец выходного порта по столбцам. Например, если перемежитель использует матрицу 2 на 3 для выполнения своих внутренних вычислений, то для входа [1 2 3 4 5 6], блок выдает выходной сигнал [1 4 2 5 3 6].
Блок Random Interleaver выбирает таблицу перестановок случайным образом, используя параметр Initial seed, предоставленный в маске блока. Используя то же начальное значение Initial в соответствующем блоке Random Deinterleaver, можно восстановить исходный порядок перестановочных символов.
Блок Алгебраического перемежителя использует таблицу перестановок, которая является алгебраически производной. Поддерживает перемежители Такешита-Костелло и перемежители Уэлча-Костаса. Эти перемежители описаны в [4].
Следующий пример иллюстрирует, как перемежитель улучшает частоту ошибок в системе связи, канал которой создает пакет ошибок. Случайный перемежитель переупорядочивает биты многочисленных кодовых слов, прежде чем каждое из двух соседних кодовых слов будет повреждено тремя ошибками.
Три ошибки превышают возможности исправления ошибок кода Хэмминга. Однако пример показывает, что когда код Хэмминга объединяется с перемежителем, эта система способна восстановить исходное сообщение, несмотря на 6-битовый пакет ошибок. Улучшение производительности происходит потому, что перемежение эффективно расширяет ошибки среди различных кодовых слов, так что количество ошибок на кодовое слово находится в пределах возможности исправления ошибок кода.
st1 = 27221; st2 = 4831; % States for random number generator n = 7; k = 4; % Parameters for Hamming code msg = randi([0 1],k*500,1); % Data to encode code = encode(msg,n,k,'hamming/binary'); % Encoded data % Create a burst error that will corrupt two adjacent codewords. errors = zeros(size(code)); errors(n-2:n+3) = [1 1 1 1 1 1]; % With Interleaving %------------------ inter = randintrlv(code,st2); % Interleave. inter_err = bitxor(inter,errors); % Include burst error. deinter = randdeintrlv(inter_err,st2); % Deinterleave. decoded = decode(deinter,n,k,'hamming/binary'); % Decode. disp('Number of errors and error rate, with interleaving:'); [number_with,rate_with] = biterr(msg,decoded) % Error statistics % Without Interleaving %--------------------- code_err = bitxor(code,errors); % Include burst error. decoded = decode(code_err,n,k,'hamming/binary'); % Decode. disp('Number of errors and error rate, without interleaving:'); [number_without,rate_without] = biterr(msg,decoded) % Error statistics
Выходные данные примера приведены ниже.
Number of errors and error rate, with interleaving:
number_with =
0
rate_with =
0
Number of errors and error rate, without interleaving:
number_without =
4
rate_without =
0.0020
В следующем примере показано, как использовать перемежитель для улучшения частоты ошибок, когда канал создает пачки ошибок.
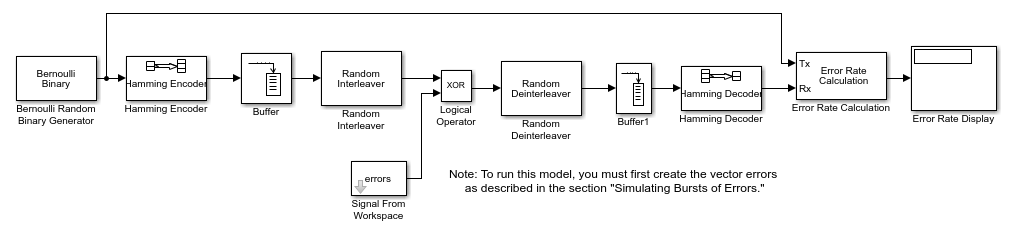
Перед запуском модели необходимо создать двоичный вектор, имитирующий пакеты ошибок, как описано в разделе Улучшение частоты ошибок с помощью перемежения блоков в Simulink. Блок «Сигнал из рабочей области» импортирует этот вектор из рабочей области MATLAB в модель, где блок «Логический оператор» выполняет исключающее ИЛИ вектора с сигналом.
Для открытия завершенной модели введите doc_interleaver в командной строке MATLAB ®. Для построения модели соберите и настройте следующие блоки:
Двоичный генератор Бернулли, в библиотеке случайных источников данных библиотеки Comm Sources
Установите флажок рядом с пунктом Выходные данные на основе кадров (Frame-based outputs).
Установить выборки для каждого кадра в значение 4.
Hamming Encoder, в блочной вспомогательной библиотеке библиотеки обнаружения и исправления ошибок. Использовать параметры по умолчанию
Буфер в поддиапазоне буферов библиотеки управления сигналами в системе DSP Toolbox™
Установить размер выходного буфера (на канал) в 84.
Случайный перемежитель (Random Interleaver) в блочной вспомогательной библиотеке библиотеки перемежения (Interleaving library in Communications) Toolbox™
Задать количество элементов для 84.
Логический оператор (Simulink) в библиотеке математических операций Simulink
Установить для оператора значение XOR.
Сигнал из рабочей области в библиотеке источников продукта DSP System Toolbox
Установить сигнал на errors.
Установить время выборки на 4/7.
Установить выборки для каждого кадра в значение 84.
Случайный обращенный перемежитель (Random Deinterleaver) в поддиапазоне блоков библиотеки перемежения в Communications Toolbox
Задать количество элементов для 84.
Буфер, в поддиапазоне Buffers библиотеки управления сигналами в панели системных инструментов DSP
Установить размер выходного буфера (на канал) в 7.
Декодер Хэмминга (Hamming Decoder) в блочной вспомогательной библиотеке библиотеки обнаружения и исправления ошибок. Используйте параметры по умолчанию.
Расчет частоты ошибок в библиотеке Comm Sinks
Установить для параметра Задержка получения значение (4/7)*84.
Установка задержки вычислений в значение 100.
Установить выходные данные в Port.
Отображение (Simulink) в библиотеке Simulink Sinks. Используйте параметры по умолчанию.
На вкладке Моделирование (Simulation) в разделе Моделирование (Simulate) задайте для параметра Время остановки (Stop time) значение length(errors). Раздел «Моделирование» отображается на нескольких вкладках.
Создание вектора ошибок. Перед запуском модели используйте следующий код для создания двоичного вектора в рабочей области MATLAB. Модель использует этот вектор для моделирования пакетов ошибок. Вектор содержит блоки по три с, представляющие пачки ошибок, через случайные интервалы. Расстояние между двумя последовательными блоками в 1 с является случайным целым числом между 1 и 80.
errors=zeros(1,10^4); n=1; while n<10^4-80; n=n+floor(79*rand(1))+3; errors(n:n+2)=[1 1 1]; end
Определение отношения числа 1 с к общему количеству символов в векторе errors войти
sum(errors)/length(errors)
Ваш ответ должен быть приблизительно 3/43, или .0698, так как после каждой последовательности из трех 1s ожидаемое расстояние до следующей последовательности из 1s равно 40. Следовательно, вы ожидаете увидеть три 1 в 43 терминах последовательности. Если бы в модели не было коррекции ошибок, частота битовых ошибок составляла бы приблизительно 0,0698.
При выполнении моделирования с моделью частота ошибок составляет приблизительно 0,019, что показывает улучшение за счет исправления ошибок и перемежения. Эффект перемежения можно увидеть, удалив блоки Random Interleaver и Random Deinterleaver из модели, соединив линии и выполнив другое моделирование. Частота битовых ошибок выше без перемежения, поскольку код Хэмминга может исправить только одну ошибку в каждом кодовом слове.
Сверточный перемежитель состоит из набора регистров сдвига, каждый из которых имеет фиксированную задержку. В типичном сверточном перемежителе задержки являются неотрицательными целыми кратными фиксированному целому числу (хотя общий мультиплексный перемежитель допускает неограниченные значения задержки). Каждый новый символ из входного вектора подается в следующий сдвиговый регистр, и самый старый символ в этом регистре становится частью выходного вектора. Сверточный перемежитель имеет память; то есть его работа зависит не только от текущих символов, но и от предыдущих символов.
Схема ниже изображает структуру общего сверточного перемежителя, показывая набор регистров сдвига и их значения задержки D (1), D (2),..., D (N). K-й сдвиговый регистр содержит D (k) символов, где k = 1,2,...,N. Функции сверточного перемежения в этой панели инструментов имеют входные аргументы, которые указывают количество сдвиговых регистров и задержку для каждого сдвигового регистра.
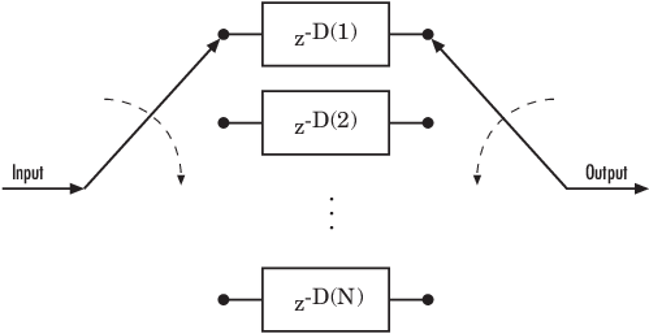
Communications Toolbox реализует функции сверточного перемежения с использованием блоков Simulink ®, системных объектов и функций MATLAB.
Набор сверточных перемежителей в этом произведении включает в себя общую пару перемежитель/обращенный перемежитель, а также несколько специальных случаев. Каждая функция специального случая использует тот же вычислительный код, что и ее более общий аналог, но обеспечивает синтаксис, который более подходит для специального случая. Особые случаи описаны ниже.
| Тип перемежителя | Функция перемежения | Описание |
|---|---|---|
| Общий мультиплексированный перемежитель | muxintrlv | Разрешает неограниченные значения задержки для набора регистров сдвига. |
| Сверточный перемежитель | convintrlv | Значения задержки для набора регистров сдвига являются неотрицательными целыми числами, кратными заданному фиксированному целому числу. |
| Спиральный перемежитель | helintrlv | Заполняет массив входными символами по спирали и очищает массив от строк. |
helscanintrlv функции и helintrlv обе функции используют спиральный массив для внутренних вычислений. Однако эти две функции имеют некоторые важные различия:
helintrlv использует массив с неограниченной строкой, размещает входные символы в массиве вдоль столбцов, выводит некоторые символы, которые не являются входными, и оставляет некоторые входные символы в массиве, не помещая их в выходные данные.
helscanintrlv использует матрицу фиксированного размера, упорядочивает входные символы в массиве по строкам и выводит все входные символы без использования значений по умолчанию или значений из предыдущего вызова.
Типы сверточных перемежителей. Набор сверточных перемежителей в этой библиотеке включает в себя общую пару перемежитель/обращенный перемежитель, а также несколько специальных случаев. Каждый блок специального случая использует тот же вычислительный код, что и его более общий аналог, но обеспечивает интерфейс, который более подходит для специального случая.
Наиболее общим блоком в этой библиотеке является блок общего мультиплексного перемежителя, который допускает произвольные значения задержки для набора регистров сдвига. Чтобы реализовать предыдущую схему с использованием этого блока, используйте параметр задержки перемежителя [D (1 ); D (2 );...; D (N)].
Более конкретно, блок сверточного перемежителя, в котором значение задержки для k-го сдвигового регистра (k-1) умножено на параметр шага длины регистра блока. Количество сдвиговых регистров в этом блоке является значением параметра Rows of shift regisers.
Наконец, блок спирального перемежителя поддерживает специальный случай сверточного перемежения, который заполняет массив символами спиральным образом и опустошает ряд массива за строкой. Чтобы настроить этот перемежитель, используйте параметр Number of columns спирального массива, чтобы задать ширину массива, и используйте параметры Group size и Helical array step size, чтобы определить, как символы размещаются в массиве. Дополнительные сведения и пример см. на справочной странице блока «Спиральный перемежитель».
После прохождения последовательности символов через сверточный перемежитель и соответствующий сверточный обращенный перемежитель восстановленная последовательность отстает от исходной последовательности. Задержка, измеренная символами, между исходной и восстановленной последовательностями указана в таблице ниже. Имена переменных во втором столбце (delay, nrows, slope, col, ngrp, и stp) см. входные данные, указанные на справочной странице каждой функции.
Задержки пар перемежителя/обращенного перемежителя
| Пара перемежителя/обращенного перемежителя | Задержка между исходной и восстановленной последовательностями |
|---|---|
muxintrlv, muxdeintrlv | length(delay)*max(delay) |
convintrlv, convdeintrlv | nrows*(nrows-1)*slope |
helintrlv, heldeintrlv | col*ngrp*ceil(stp*(col-1)/ngrp) |
Задержки сверточных перемежителей. После прохождения последовательности символов через сверточный перемежитель и соответствующий сверточный обращенный перемежитель восстановленная последовательность отстает от исходной последовательности. Задержка, измеренная символами, между исходной и восстановленной последовательностями составляет
Число регистров сдвига × Максимальная задержка среди всех регистров сдвига
для наиболее общего мультиплексированного перемежителя. Если модель несет дополнительную задержку между выходом перемежителя и входом обращенного перемежителя, восстановленная последовательность отстает от исходной последовательности на сумму дополнительной задержки и величину в предыдущей формуле.
Примечание
Для правильной синхронизации задержка в модели между выходом перемежителя и входом обращенного перемежителя должна быть целочисленной кратной числу сдвиговых регистров. При необходимости можно использовать блок задержки панели инструментов DSP для настройки задержек вручную.
Сверточный блок перемежителя
В частном случае, реализуемом сверточным перемежителем/сверточным обращенным перемежителем, число регистров сдвига является параметром Rows регистров сдвига, в то время как максимальная задержка среди всех регистров сдвига равна
B × (N-1)
где B - параметр шага длины регистра, а N - параметр строк регистров сдвига.
Блок спирального перемежителя
В частном случае, реализуемом парой спирального перемежителя/спирального обращенного перемежителя, задержка между восстановленной последовательностью и исходной последовательностью равна
) N ⌉
где C - число столбцов в параметре спирального массива, N - параметр размера группы, а s - параметр размера шага спирального массива.
Влияние задержек на восстановление сверточно перемежающихся данных с использованием MATLAB. Если используется сверточный перемежитель, за которым следует соответствующий сверточный обращенный перемежитель, то ненулевая задержка означает, что восстановленные данные (то есть выходные данные обращенного перемежителя) не совпадают с исходными данными (то есть входными данными перемежителя). При непосредственном сравнении двух наборов данных необходимо учитывать задержку, используя соответствующие операции усечения или заполнения.
Вот несколько типичных способов компенсации задержки D в паре перемежитель/обращенный перемежитель:
Перемежайте версию исходных данных, дополненную дополнительными символами D в конце. Прежде чем сравнивать исходные данные с восстановленными данными, опустите первые D символов восстановленных данных. При таком подходе все исходные символы появляются в восстановленных данных.
Перед сравнением исходных данных с восстановленными данными опустите последние D символов исходных данных и первые D символов восстановленных данных. В этом подходе некоторые из исходных символов остаются в сдвиговых регистрах обращенного перемежителя и не появляются в восстановленных данных.
Следующий код иллюстрирует эти подходы путем вычисления частоты ошибок символов для операции перемежения/обращенного перемежения.
x = randi([0 63],20,1); % Original data nrows = 3; slope = 2; % Interleaver parameters D = nrows*(nrows-1)*slope; % Delay of interleaver/deinterleaver pair hInt = comm.ConvolutionalInterleaver('NumRegisters', nrows, ... 'RegisterLengthStep', slope); hDeint = comm.ConvolutionalDeinterleaver('NumRegisters', nrows, ... 'RegisterLengthStep', slope); % First approach. x_padded = [x; zeros(D,1)]; % Pad x at the end before interleaving. a1 = step(hInt, x_padded); % Interleave padded data. b1 = step(hDeint, a1) % Omit input padding and the first D symbols of the recovered data and % compare servec1 = step(comm.ErrorRate('ReceiveDelay',D),x_padded,b1); ser1 = servec1(1) % Second approach. release(hInt); release(hDeint) a2 = step(hInt,x); % Interleave original data. b2 = step(hDeint,a2) % Omit the last D symbols of the original data and the first D symbols of % the recovered data and compare. servec2 = step(comm.ErrorRate('ReceiveDelay',D),x,b2); ser2 = servec2(1)
Выходные данные показаны ниже. Нулевые значения ser1 и ser2 указать, что сценарий правильно выровнял исходные и восстановленные данные перед вычислением коэффициентов ошибок символов. Однако обратите внимание на длину b1 и b2 что два подхода к выравниванию приводят к различным объемам данных с обращенным перемежением.
b1 =
0
0
0
0
0
0
0
0
0
0
0
0
59
42
1
28
52
54
43
8
56
5
35
37
48
17
28
62
10
31
61
39
ser1 =
0
b2 =
0
0
0
0
0
0
0
0
0
0
0
0
59
42
1
28
52
54
43
8
ser2 =
0
Объединение задержек перемежения и других задержек. Если вы используете сверточные перемежители в сценарии, который несет дополнительную задержку, d, между выходом перемежителя и входом обращенного перемежителя (например, задержка от фильтра), то восстановленная последовательность отстает от исходной последовательности на сумму d и величину из таблицы Задержки пар перемежителя/обращенного перемежителя. В этом случае d должно быть целым числом, кратным числу сдвиговых регистров, иначе сверточный обращенный перемежитель не сможет правильно восстановить исходные символы. Если d не является, естественно, целым числом, кратным числу сдвиговых регистров, то можно настроить задержку вручную, заполняя вектор, который формирует вход в обращенный перемежитель.
Пример ниже иллюстрирует сверточное перемежение и обращенное перемежение с использованием последовательности последовательных целых чисел. Он также иллюстрирует внутреннюю задержку пары перемежитель/обращенный перемежитель.
x = [1:10]'; % Original data delay = [0; 1; 2]; % Set delays of three shift registers. hInt = comm.MultiplexedInterleaver('Delay', delay); hDeint = comm.MultiplexedDeinterleaver('Delay', delay); y = step(hInt,x) % Interleave. z = step(hDeint,y) % Deinterleave.
В этом примере muxintrlv функция инициализирует три регистра сдвига по значениям [], [0], и [0 0]соответственно. Затем функция обрабатывает входные данные. [1:10]', выполнение внутренних вычислений, как указано в таблице ниже.
| Текущий вход | Текущий регистр смены | Токовый выход | Содержимое регистров сдвига | |||
|---|---|---|---|---|---|---|
1 | 1 | 1 |
| |||
2 | 2 | 0 |
| |||
3 | 3 | 0 |
| |||
4 | 1 | 4 |
| |||
5 | 2 | 2 |
| |||
6 | 3 | 0 |
| |||
7 | 1 | 7 |
| |||
8 | 2 | 5 |
| |||
9 | 3 | 3 |
| |||
10 | 1 | 10 |
|
Выходные данные примера приведены ниже.
y =
1
0
0
4
2
0
7
5
3
10
state_y =
value: {3x1 cell}
index: 2
z =
0
0
0
0
0
0
1
2
3
4
Обратите внимание, что столбец «Current Output» в таблице выше совпадает со значениями в векторе. y. Кроме того, последняя строка таблицы выше указывает, что последний сдвиговый регистр, обработанный для данного набора данных, является первым сдвиговым регистром. Это согласуется со значением 2 для state_y.index, которая указывает, что любые дополнительные входные данные будут направлены во второй сдвиговый регистр. При необходимости можно проверить, что значения состояния перечислены в state_y.value сопоставить запись «Contents of Shift Regists» в последней строке таблицы путем ввода state_y.value{:} в окне команд после выполнения примера.
Другой особенностью, которая должна быть замечена в примере вывода, является то, что z содержит шесть нулей в начале перед содержанием любого из символов из исходного набора данных. Шесть нулей иллюстрируют, что задержка этой пары сверточный перемежитель/обращенный перемежитель равна length(delay)*max(delay) = 3*2 = 6. Дополнительные сведения о задержках см. в разделе Задержки сверточных перемежителей.
Пример ниже иллюстрирует сверточное перемежение и обращенное перемежение с использованием последовательности последовательных целых чисел. Он также иллюстрирует внутреннюю задержку и влияние начальных условий перемеживающих блоков.
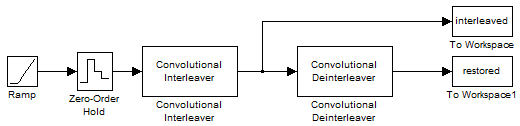
Для открытия модели введите doc_convinterleaver в командной строке MATLAB. Для построения модели соберите и настройте следующие блоки:
Пандус (Simulink), в библиотеке Simulink Sources. Используйте параметры по умолчанию.
Удержание нулевого порядка (Simulink) в библиотеке дискретных Simulink. Используйте параметры по умолчанию.
Задать для строк регистров сдвига значение 3.
Установить начальные условия в значение [-1 -2 -3]'.
Сверточный обращенный перемежитель
Задать для строк регистров сдвига значение 3.
Установить начальные условия в значение [-1 -2 -3]'.
Две копии в рабочей области (Simulink) в библиотеке Simulink Sinks
Задать для имени переменной значение interleaved и restoredсоответственно в двух копиях этого блока.
Задать для параметра «Сохранить формат» значение Array в каждой из двух копий этого блока.
Подключите блоки, как показано на предыдущем рисунке. На вкладке Моделирование (Simulation) в разделе Моделирование (Simulate) задайте для параметра Время остановки (Stop time) значение 20. Раздел «Моделирование» отображается на нескольких вкладках. Запустите моделирование и выполните следующую команду:
comparison = [[0:20]', interleaved, restored]
comparison =
0 0 -1
1 -2 -2
2 -3 -3
3 3 -1
4 -2 -2
5 -3 -3
6 6 -1
7 1 -2
8 -3 -3
9 9 -1
10 4 -2
11 -3 -3
12 12 0
13 7 1
14 2 2
15 15 3
16 10 4
17 5 5
18 18 6
19 13 7
20 8 8
В этом выводе первый столбец содержит исходную последовательность символов. Второй столбец содержит чередующуюся последовательность, в то время как третий столбец содержит восстановленную последовательность.
Отрицательные числа в перемеженных и восстановленных последовательностях происходят из начальных условий блоков перемежения, а не из исходных данных. Первый из исходных символов появляется в восстановленной последовательности только после задержки в 12 символов. Задержка комбинации перемежитель-обращенный перемежитель является произведением количества сдвиговых регистров (3) и максимальной задержки среди всех сдвиговых регистров (4).
Аналогичный пример, который также указывает содержимое сдвиговых регистров на каждом этапе процесса, см. в разделе Сверточное перемежение и обратное перемежение с использованием последовательности последовательных целых чисел в MATLAB.
Берлекамп, E.R. и P. Tong, «Улучшенные перемежители для алгебраических блочных кодов», патент США 4559625, 17 декабря 1985 г.
[2] Кларк, Джордж К. младший и Дж. Бибб Кейн, кодирование с исправлением ошибок для цифровых коммуникаций, Нью-Йорк, Plenum Press, 1981.
[3] Форни, Г. Д. младший, «Burst-Correcting Codes for the Classic Bursty Channel», IEEE Transactions on Communications, vol. COM-19, October 1971, pp. 772-781.
[4] Хигард, Крис и Стивен Б. Викер, Turbo Coding, Boston, Kluwer Academic Publishers, 1999.
[5] Рэмзи, J. L, «Реализация оптимальных перемежителей», IEEE Transactions on Information Theory, IT-16 (3), май 1970, стр. 338-345.
[6] Такешита, О. Я. и Д. Дж. Костелло, младший, «Новые классы алгебраических перемежителей для турбокодов», Proc. 1998 IEEE Международный симпозиум по теории информации, Бостон, 16-21 августа 1998 года. стр 419.