Проектирование фильтра Калмана для оценки состояния
[ создает фильтр Калмана для модели установки kalmf,L,P] = kalman(sys,Q,R,N)sys и данные ковариации шума Q, R, и N. Функция вычисляет фильтр Калмана для использования в оценщике Калмана с конфигурацией, показанной на следующей диаграмме.
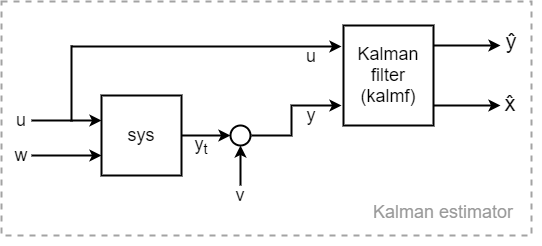
Построение модели sys с известными входами u и входами белого технологического шума w, так что w состоит из последних входов Nw в sys. «Истинный» выход установки yt состоит из всех выходов sys. Вы также предоставляете данные ковариации шума Q, R, и N. Возвращенный фильтр Калмана kalmf является моделью состояния-пространства, которая принимает известные входы u и шумные измерения y и производит оценку ^ истинного выхода растения и оценку ^ состояний растения.kalman также возвращает выигрыш Калмана L и ковариационная матрица ошибки стационарного состояния P.
[ вычисляет фильтр Калмана при наличии одного или обоих следующих условий.kalmf,L,P] = kalman(sys,Q,R,N,sensors,known)
Не все выходы sys измеряют.
Входы возмущения w не являются последними входами sys.
Вектор индекса sensors определяет, какие выходы sys измеряют. Эти выходы составляют y. Вектор индекса known указывает, какие входные данные известны (детерминированы). Известные входные данные составляют u. kalman команда принимает остальные входы sys быть стохастическими входами w.
[ определяет тип оценщика для дискретного времени kalmf,L,P,Mx,Z,My] = kalman(___,type)sys.
type = 'current' Вычисляют выходные оценки n 'n] и состояния
type = 'delayed' - Вычислить выходные оценки − 1] и состояния
Вы можете использовать type входной аргумент с любой из предыдущих комбинаций входных аргументов.
Спроектируйте фильтр Калмана для установки с добавочным белым шумом w на входе и v на выходе, как показано на следующей диаграмме.
Предположим, что установка имеет следующие матрицы состояния-пространства и является установкой дискретного времени с неопределенным временем выборки (Ts = -1).
A = [1.1269 -0.4940 0.1129
1.0000 0 0
0 1.0000 0];
B = [-0.3832
0.5919
0.5191];
C = [1 0 0];
D = 0;
Plant = ss(A,B,C,D,-1);
Plant.InputName = 'un';
Plant.OutputName = 'yt';Использовать kalman, необходимо предоставить модель sys который имеет вход для шума w. Таким образом, sys не совпадает с Plant, потому что Plant принимает входные данные un = u + w. Можно построить sys путем создания суммирующего перехода для входного шума.
Sum = sumblk('un = u + w'); sys = connect(Plant,Sum,{'u','w'},'yt');
Эквивалентно, вы можете использовать sys = Plant*[1 1].
Укажите ковариации шума. Поскольку установка имеет один вход шума и один выход, эти значения являются скалярными. На практике эти значения являются свойствами источников шума в системе, которые определяются измерением или другим знанием системы. В этом примере предположим, что оба источника шума имеют единичную ковариацию и не коррелированы (N = 0).
Q = 1; R = 1; N = 0;
Спроектируйте фильтр.
[kalmf,L,P] = kalman(sys,Q,R,N); size(kalmf)
State-space model with 4 outputs, 2 inputs, and 3 states.
Фильтр Кальмана kalmf - модель состояния-пространства, имеющая два входа и четыре выхода. kalmf принимает в качестве входов входной сигнал u установки и выходной сигнал шумной установки kalmf чтобы увидеть, как kalman маркирует их соответствующим образом.
kalmf.InputName
ans = 2x1 cell
{'u' }
{'yt'}
kalmf.OutputName
ans = 4x1 cell
{'yt_e'}
{'x1_e'}
{'x2_e'}
{'x3_e'}
Изучить завоевания Калмана L. Для установки SISO с тремя состояниями, L является вектором трехэлементного столбца.
L
L = 3×1
0.3586
0.3798
0.0817
Пример использования kalmf об уменьшении погрешности измерений из-за шума см. в разделе Фильтрация Калмана.
Рассмотрим установку с тремя входами, один из которых представляет технологический шум w, и двумя измеренными выходами. Завод имеет четыре состояния.
Предположим, что следующие матрицы состояния-пространства, создать sys.
A = [-0.71 0.06 -0.19 -0.17;
0.06 -0.52 -0.03 0.30;
-0.19 -0.03 -0.24 -0.02;
-0.17 0.30 -0.02 -0.41];
B = [ 1.44 2.91 0;
-1.97 0.83 -0.27;
-0.20 1.39 1.10;
-1.2 0 -0.28];
C = [ 0 -0.36 -1.58 0.28;
-2.05 0 0.51 0.03];
D = zeros(2,3);
sys = ss(A,B,C,D);
sys.InputName = {'u1','u2','w'};
sys.OutputName = {'y1','y2'};Поскольку установка имеет только один входной сигнал технологического шума, ковариация Q является скалярной. В этом примере предположим, что шум процесса имеет единичную ковариацию.
Q = 1;
kalman использует размеры Q для определения, какие входы известны, а какие являются входами шума. Для скаляра Q, kalman предполагает один вход шума и использует последний вход, если не указано иное (см. Установка с неизмеряемыми выходами).
Для измерения шума на двух выходах задайте ковариационную матрицу шума 2 на 2. Для этого примера используйте единичную дисперсию для первого выхода и дисперсию 1,3 для второго выхода. Установите значения вне диагонали на ноль, чтобы указать, что два шумовых канала не коррелированы.
R = [1 0;
0 1.3];Спроектируйте фильтр Калмана.
[kalmf,L,P] = kalman(sys,Q,R);
Осмотрите входы и выходы. kalman использует InputName, OutputName, InputGroup, и OutputGroup свойства kalmf чтобы помочь вам отслеживать, какие входы и выходы kalmf представляют.
kalmf.InputGroup
ans = struct with fields:
KnownInput: [1 2]
Measurement: [3 4]
kalmf.InputName
ans = 4x1 cell
{'u1'}
{'u2'}
{'y1'}
{'y2'}
kalmf.OutputGroup
ans = struct with fields:
OutputEstimate: [1 2]
StateEstimate: [3 4 5 6]
kalmf.OutputName
ans = 6x1 cell
{'y1_e'}
{'y2_e'}
{'x1_e'}
{'x2_e'}
{'x3_e'}
{'x4_e'}
Таким образом, два известных входа u1 и u2 являются первыми двумя входами kalmf и два измеренных выхода y1 и y2 являются двумя последними входами в kalmf. Для выходных данных kalmfпервые два являются оценочными выходами, а остальные четыре являются оценками состояния. Чтобы использовать фильтр Калмана, подключите эти входы к установке и шумовым сигналам способом, аналогичным показанному для установки SISO в Kalman Filtering.
Рассмотрим установку с четырьмя входами и двумя выходами. Первый и третий входы известны, в то время как второй и четвертый входы представляют шум процесса. Завод также имеет два выхода, но измеряется только второй из них.
Используйте следующие матрицы состояния-пространства для создания sys.
A = [-0.37 0.14 -0.01 0.04;
0.14 -1.89 0.98 -0.11;
-0.01 0.98 -0.96 -0.14;
0.04 -0.11 -0.14 -0.95];
B = [-0.07 -2.32 0.68 0.10;
-2.49 0.08 0 0.83;
0 -0.95 0 0.54;
-2.19 0.41 0.45 0.90];
C = [ 0 0 -0.50 -0.38;
-0.15 -2.12 -1.27 0.65];
D = zeros(2,4);
sys = ss(A,B,C,D,-1); % Discrete with unspecified sample time
sys.InputName = {'u1','w1','u2','w2'};
sys.OutputName = {'yun','ym'};Использовать kalman чтобы разработать фильтр для этой системы, используйте known и sensors входные аргументы для указания, какие входы в установку известны, а какие измеряются.
known = [1 3]; sensors = [2];
Укажите ковариации шума и спроектируйте фильтр.
Q = eye(2); R = 1; N = 0; [kalmf,L,P] = kalman(sys,Q,R,N,sensors,known);
Изучение входных и выходных меток kalmf показывает входные данные, которые ожидает фильтр, и выходные данные, которые он возвращает.
kalmf.InputGroup
ans = struct with fields:
KnownInput: [1 2]
Measurement: 3
kalmf.InputName
ans = 3x1 cell
{'u1'}
{'u2'}
{'ym'}
kalmf принимает в качестве входов два известных входа sys и шумные измеренные выходы sys.
kalmf.OutputGroup
ans = struct with fields:
OutputEstimate: 1
StateEstimate: [2 3 4 5]
Первый выход kalmf - его оценка истинного значения измеренной производительности установки. Остальные результаты являются оценками состояния.
sys - Модель установки с технологическим шумомss модельМодель установки с технологическим шумом, заданная как состояние-пространство (ss) модель. Завод имеет известные входы u и белые входы технологического шума w. Выход завода yt не включает шум измерения.
Можно записать матрицы состояния-пространства такой модели растения, как:
H]
kalman принимает гауссов шум v на выходе. Таким образом, в непрерывном времени, состояние-пространство уравнений, что kalman работы с:
Hw + v
За дискретное время уравнения состояния и пространства:
+ Du [n] + Hw [n] + v [n]
Если вы не используете known входной аргумент, kalman использует размер Q определить, какие входы sys являются входами шума. В этом случае kalman обрабатывает последнее Nw = size(Q,1) входы в качестве входов шума. Когда входы шума w не являются последними входами sys, вы можете использовать known входной аргумент для указания того, какие заводские входы известны. kalman рассматривает остальные входные данные как стохастические.
Дополнительные ограничения свойств матриц растений см. в разделе Ограничения.
Q - Ковариация технологического шумаКовариация шума процесса, заданная как скалярная или матрица Nw-by-Nw, где Nw - количество входов шума в установку. kalman использует размер Q определить, какие входы sys являются входами шума, принимая последнее Nw = size(Q,1) входы должны быть входами шума, если не указано иное с помощью known входной аргумент.
kalman предполагает, что технологический шум w является гауссовым шумом с ковариацией Q = E (wwT). Если установка имеет только один входной сигнал технологического шума ,Q является скаляром, равным дисперсии w. Когда установка имеет несколько, некоррелированных входов шума, Q - диагональная матрица. На практике определяются соответствующие значения для Q измеряя или делая обоснованные догадки о шумовых свойствах вашей системы.
R - Ковариация шума измеренияКовариация шума измерения, заданная как скалярная или матрица Ny-by-Ny, где Ny - количество выходов установки. kalman предполагает, что измеряемый шум v является белым шумом с ковариацией R = E (vvT). Если установка имеет только один выходной канал ,R является скаляром, равным дисперсии v. Когда установка имеет несколько выходных каналов с некоррелированным шумом измерения, R - диагональная матрица. На практике определяются соответствующие значения для R измеряя или делая обоснованные догадки о шумовых свойствах вашей системы.
Дополнительные ограничения ковариации шума измерений см. в разделе Ограничения.
N - Перекрестная ковариация шумаПерекрестная ковариация шума, заданная как скалярная или матрица Ny-by-Nw. kalman предполагает, что технологический шум w и измерительный шум v удовлетворяют N = E (wvT). Если два источника шума не коррелированы, их можно опуститьN, что эквивалентно установке N = 0. На практике определяются соответствующие значения для N измеряя или делая обоснованные догадки о шумовых свойствах вашей системы.
sensors - Измеренные выходы sysИзмеренные выходы sys, указанный как вектор индексов, идентифицирующих, какие выходы sys измеряют. Например, предположим, что ваша система имеет три выхода, но только два из них измеряются, что соответствует первому и третьему выходам sys. В этом случае установить sensors = [1 3].
known - Известные входы sysИзвестные входы sys, указанный как вектор индексов, идентифицирующих, какие входные данные известны (детерминированы). Например, предположим, что система имеет три входа, но известны только первый и второй. В этом случае установить known = [1 2]. kalman интерпретирует любые оставшиеся входы sys быть стохастическим.
type - Тип дискретно-временной оценки'current' (по умолчанию) | 'delayed'Тип вычисляемого дискретно-временного оценщика, указанный как 'current' или 'delayed'. Этот вход релевантен только для дискретного времени sys.
'current' Вычисляют выходные оценки n 'n] и состояния
'delayed' - Вычислить выходные оценки − 1] и состояния
Для получения подробной информации о том, как kalman вычисляет текущую и задержанную оценки, см. Дискретная оценка времени.
kalmf - Калмановский оценщикss модельКалман-оценщик или калман-фильтр, возвращенный как состояние-пространство (ss) модель. Результирующий оценщик имеет входы ] и выходы x ^]. Другими словами,kalmf принимает в качестве входных сигналов входной сигнал u установки и выходной сигнал y установки с шумом и выдает в качестве выходных сигналов расчетный выходной сигнал ^ установки без шума и расчетные значения ^ состояния.
kalman автоматически устанавливает InputName, OutputName, InputGroup, и OutputGroup свойства kalmf помогает отслеживать, какие входы и выходы соответствуют каким сигналам.
Для уравнений состояния и выхода kalmf, см. Непрерывная оценка времени и Дискретная оценка времени.
L - Коэффициент усиления фильтраКоэффициенты усиления фильтра, возвращаемые как массив размера Nx-by-Ny, где Nx - количество состояний в установке, а Ny - количество выходов установки. За непрерывное время уравнение состояния фильтра Калмана составляет:
− Du).
За дискретное время уравнение состояния:
− Cx ^ [n' n − 1] − Du [n]).
Дополнительные сведения об этих выражениях и способах L вычисляется, см. Непрерывная оценка времени и Дискретная оценка времени.
P, Z - Ковариации ошибок стационарного состоянияКовариации ошибок стационарного состояния, возвращаемые как Nx-by-Nx, где Nx - количество состояний в установке. Фильтр Калмана вычисляет оценки состояния, которые минимизируют P. Через непрерывное время ковариация ошибки установившегося состояния задается следующим образом:
x ^} T).
За дискретное время ковариации погрешности установившегося состояния задаются:
[n 'n]} {x [n] − x ^ [n' n]} T).
Для получения дополнительной информации об этих количествах и способах kalman использует их, см. Непрерывная оценка времени и Дискретная оценка времени.
Mx, My - Инновационный выигрыш государственных оценщиковИнновационный выигрыш оценщиков состояния для дискретно-временных систем, возвращаемый в виде массива.
Mx и My релевантны только тогда, когда type = 'current', который является оценщиком по умолчанию для систем дискретного времени. Для непрерывного времени sys или type = 'delayed', то Mx = My = [].
Для 'current' оценщик типа, Mx и My являются ли достижения инноваций в уравнениях обновления:
^ [n 'n − 1] − Du [n])
Cx ^ [n 'n − 1] − Du [n])
Когда отсутствует прямой проход от входа шума w к выходу установки y (то есть когда H = 0, см. Дискретная оценка времени), то CMx, и выходная оценка упрощается n' n] + Du [n].
Размеры массивов Mx и My зависят от размеров sys следующим образом.
Mx - Nx-by-Ny, где Nx - количество состояний в установке, а Ny - количество выходов.
My - Ny-by-Ny.
Для получения подробной информации о том, как kalman получает Mx и My, см. Дискретная оценка времени.
Данные по установке и шуму должны удовлетворять:
(C, A) обнаруживается, где:
> 0 N¯′R¯]≥0, где
′.
N пр Р пр − 1N Т) не имеет неуправляемого режима на воображаемой оси за непрерывное время или на единичной окружности за дискретное время.