Линейная изменяющая параметры (LPV) система - это линейная модель состояния-пространства, динамика которой изменяется как функция определенных изменяющихся во времени параметров, называемых параметрами планирования. В MATLAB ® модель LPV представлена в форме state-space с использованием коэффициентов, зависящих от параметра.
Математически система LPV представлена как:
| t) + D (p) u (t) x (0) = x0 | (1) |
где
u(t) являются входами
y(t) продукция
x(t) являются состояниями модели с начальным значением x0
) - вектор производной состояния, x˙ для систем непрерывного времени, и вектор обновления состояния ΔT) для систем дискретного времени. ΔT - время выборки.
A(p), B(p), C(p) и D(p) - матрицы состояния-пространства, параметризованные вектором параметров планирования p.
Параметры p = p(t) - измеримые функции входных данных и состояния модели. Они могут быть скалярной величиной или вектором нескольких параметров. Набор параметров планирования определяет пространство планирования, в котором определяется модель LPV.
Общим способом представления моделей LPV является интерполированный массив линейных моделей состояния-пространства. Выбирается определенное количество точек в пространстве планирования, обычно образуя обычную сетку. Каждой точке назначается система LTI, представляющая динамику в локальной окрестности этой точки. Динамика в местоположениях планирования между точками сетки получается путем интерполяции систем LTI в соседних точках.
Например, аэродинамическое поведение летательного аппарата часто планируется по сетке значений угла падения (α) и скорости ветра (V). Для каждого параметра планирования выбирается диапазон значений, таких как α = 0:5:20 градусов, V = 700:100:1400 м/с. Для каждой комбинации значений (α, V) получается линейная аппроксимация поведения самолета. Локальные модели соединены, как показано на следующем рисунке:
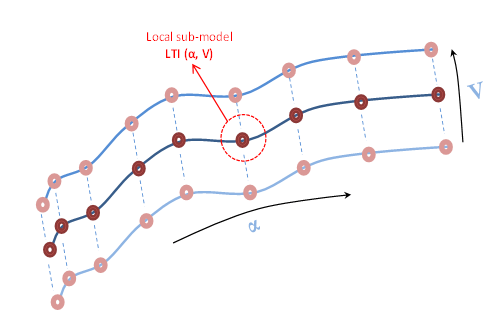
Каждый пончик представляет локальную модель LTI, а соединительные кривые представляют правила интерполяции. Абсцисса и ордината поверхности являются параметрами планирования (α, V).
Эту форму иногда называют представлением LPV на основе сетки. Это форма, используемая блоком системы LPV. Для значимых интерполяций системных матриц все локальные модели должны использовать один и тот же базис состояний.
Представление системы LPV может быть расширено, чтобы разрешить смещения в dx, x, u и y переменные. Эта форма известна как аффинная форма модели LPV. Математически ниже представлена система LPV:
| y¯ (p) −C (p) x¯ (p) −D (p) u¯ (p)) x (0) =x0 | (2) |
(p) - смещения в значенияхdx(t), x(t), u(t) и y(t) при заданном значении параметра p = p(t).
Чтобы получить такие представления массива линейной системы, линеаризуйте модель Simulink ® над пакетом рабочих точек (см. Пакетная линеаризация (Simulink Control Design).) Смещения соответствуют рабочим точкам, в которых линеаризована модель.
Смещения можно получить, вернув дополнительную информацию линеаризации при вызове функций, таких как linearize (Simulink Control Design) или getIOTransfer(Проект управления симуляцией). Затем можно извлечь смещения с помощью getOffsetsForLPV(Проект управления симуляцией). Пример см. в разделе Аппроксимация LPV модели Boost Converter (Simulink Control Design).
В аффинном представлении линейная модель в данной точке p = p* в области планирования:
(p *) Δx (t, p *) + D (p *) Δu (t, p *)
Состояния этой линейной модели связаны с состояниями общей модели LPV (уравнение 2) по − x (p *). *) = и Δu (t, p *) = u (t) − u (p *).
Рассмотрим систему, которая использует два параметра планирования, α и β. Когда α и β меняются монотонно, образуется правильная сетка, как показано на следующем рисунке. Массив пространств состояний содержит значение при каждой комбинации значений α и β. Регулярная сетка не предполагает равномерного интервала между значениями.

Когда параметры совместно изменяются, то есть α и β увеличиваются вместе, образуется неправильная сетка. Параметры массива системы доступны только по диагонали в плоскости параметров.
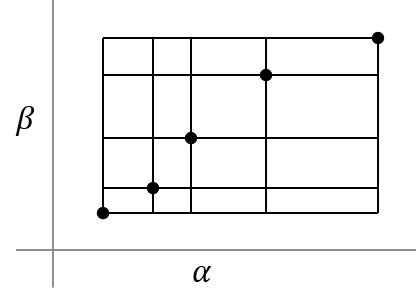
Если некоторые образцы отсутствуют в другой обычной сетке, сетка считается нерегулярной.

Массив непротиворечивых по состоянию линейных моделей, определяющих модель LPV, представлен массивом объектов модели состояния-пространства. Дополнительные сведения о массивах моделей см. в разделе Массивы моделей.
Размер системного массива равен размеру сетки в пространстве планирования. В примере самолета α принимает 5 значений в диапазоне 0-20 градусов и V принимает 8 значений в диапазоне 700-1400 м/с. При определении линейной модели при каждой комбинации значений (α, V) (т.е. сетка является обычной) размер сетки равен 5 на 8. Поэтому размер массива модели должен быть 5 на 8.
Информация о параметрах планирования присоединяется к массиву линейной модели с помощью его SamplingGrid собственность. Значение SamplingGrid свойство должно быть структурой, содержащей столько полей, сколько имеется параметров планирования. Для каждого поля значение должно быть установлено на все значения, принятые соответствующей переменной в области планирования.
Для примера самолета можно определить SamplingGrid свойство как:
Alpha = 0:5:20; V = 700:100:1400; [Alpha_Grid,V_Grid] = ndgrid(Alpha, V); linsysArray.SamplingGrid = struct('Alpha',Alpha_Grid,'V',V_Grid);
Точно так же, как линейная модель обеспечивает аппроксимацию поведения системы при заданном рабочем состоянии, модель LPV обеспечивает аппроксимацию поведения на участке на рабочих условиях. Общим подходом к построению модели LPV является пакетная обрезка и линеаризация с последующей укладкой локальных моделей в массив модели «состояние-пространство».
Примечание
При получении линейных моделей путем линеаризации не уменьшайте и не изменяйте переменные состояния, используемые моделями.
Операционная область обычно имеет большую размерность, поскольку состоит из всех входных переменных и переменных состояния. Генерирование или интерполяция локальных моделей в таких многомерных пространствах обычно неосуществимы. Более простой подход заключается в использовании небольшого набора параметров планирования в качестве прокси для переменных операционной области. Параметры планирования получают из входных данных и переменных состояния исходной системы. Необходимо тщательно выбирать значения, чтобы для фиксированного значения параметров планирования поведение системы было приблизительно линейным. Такой подход не всегда возможен.
Рассмотрим нелинейную систему, описанную следующими уравнениями:
2
Предположим, что в качестве переменной планирования используется p (t) = x˙1. В данный момент времени t = t0, у вас есть:
x˙2=−2x1−3x2+2uy= x1 + 2
Таким образом, динамика линейна (аффинна) в окрестности заданного значения . Аппроксимация сохраняется для всех интервалов времени и значений входного сигнала u до тех пор, пока не сильно отклоняется от своего номинального значения в точке t0 выборки. Следует отметить, что планирование по входам u или состояниям x1 или x2 не способствует локальной линеаризации системы. Поэтому они не являются хорошими кандидатами для параметров планирования.
Пример этого подхода см. в разделе Аппроксимация нелинейного поведения с использованием массива систем LTI (Simulink Control Design).
Модели LPV можно использовать для представления систем с несколькими режимами работы. Примеры таких систем включают в себя столкнувшиеся тела, системы, управляемые переключателями оператора, и аппроксимации систем, подверженных воздействию сухого трения и гистерезиса. Пример см. в разделе Использование массивов LTI для моделирования многорежимной динамики.
Этот подход полезен для создания суррогатных моделей, которые можно использовать вместо исходной системы для ускорения моделирования, уменьшения объема памяти целевого аппаратного кода и моделирования аппаратного обеспечения в цикле (HIL). Можно также использовать суррогатные модели этого типа для проектирования контроллеров с планированием усиления и для инициализации задач оценки параметров в Simulink. Пример аппроксимации общего нелинейного поведения системы с помощью модели LPV см. в разделе Аппроксимация нелинейного поведения с использованием массива систем LTI (Simulink Control Design).
Модели LPV могут помочь ускорить моделирование систем на основе физических компонентов, таких как системы, построенные с использованием программного обеспечения Simscape™ Multibody™ и Simscape Electrical™ Power Systems. Пример этого подхода см. в разделе Аппроксимация LPV модели Boost Converter (Simulink Control Design).
Система LPV | getOffsetsForLPV (Simulink Control Design)