Например,
circle = rsmak('circle');
обеспечивает рациональный сплайн, значения которого на его базовом интервале отслеживают единичную окружность, т.е. окружность радиуса 1 с центром в начале координат, в качестве команды
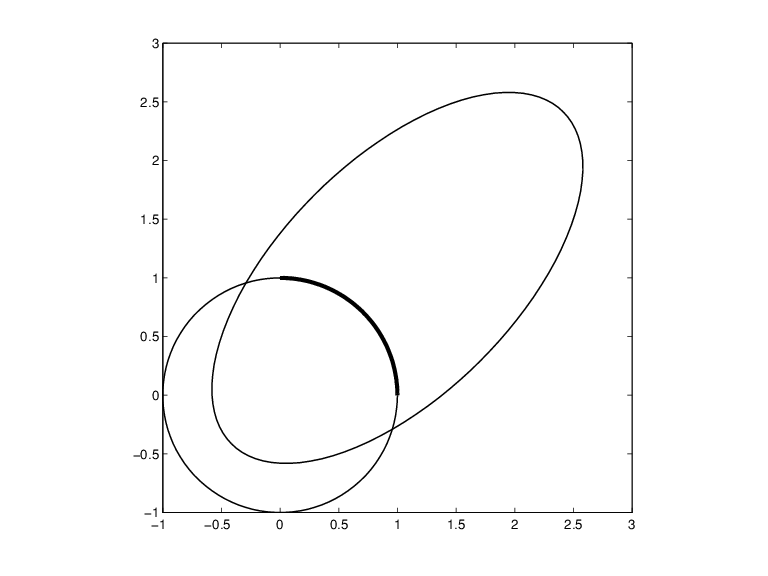
fnplt(circle), axis square
легко показывает; результатом является окружность на рисунке A Circle (круг) и эллипс (эллипс), задаваемые рациональным сплайном.
Легко манипулировать этой окружностью для получения связанных фигур. Например, следующие команды растягивают окружность на эллипс, поворачивают эллипс на 45 градусов и перемещают его на (1,1), а затем строят график поверх окружности.
ellipse = fncmb(circle,[2 0;0 1]); s45 = 1/sqrt(2); rtellipse = fncmb(fncmb(ellipse, [s45 -s45;s45 s45]), [1;1] ); hold on, fnplt(rtellipse), hold off
В качестве дополнительного примера, только что построенный «круг» складывается из четырех частей. Чтобы выделить первый такой участок, используйте следующие команды:
quarter = fnbrk(fn2fm(circle,'rp'),1); hold on, fnplt(quarter,3), hold off
В первой команде fn2fm используется для изменения форм с одной на основе B-формы на другую на основе ppform, а затем fnbrk используется для извлечения первого участка, и этот участок затем наносится на график поверх круга в виде круга и эллипса, которые задаются рациональным сплайном, с шириной линии 3 чтобы это выделялось.
Круг и эллипс, задаваемые рациональным сплайном
В качестве примера поверхности используйте команду rsmak('southcap') обеспечивает 3-векторное значение рационального бикубического многочлена, значения которого на единичном квадрате [-1.. 1] ^ 2 заполнить часть единичной сферы. Примыкайте к нему пять подходящих оборотов его и вы получите единицу сферы точно. Для иллюстрации, следующие команды генерируют две трети этой сферы, как показано в разделе Часть сферы, образованной четырьмя вращениями квартальной рациональной.
southcap = rsmak('southcap'); fnplt(southcap)
xpcap = fncmb(southcap,[0 0 -1;0 1 0;1 0 0]);
ypcap = fncmb(xpcap,[0 -1 0; 1 0 0; 0 0 1]);
northcap = fncmb(southcap,-1);
hold on, fnplt(xpcap), fnplt(ypcap), fnplt(northcap)
axis equal, shading interp, view(-115,10), axis off, hold off
Часть сферы, образованной четырьмя вращениями квартальной рациональной

Выбрав представление рационального сплайна r = s/w таким образом обычным сплайном R = [s; w] делает его легко применить к рациональному сплайну все fn... в функциях «Фитинг кривой» Toolbox™ «Сплайн» со следующими исключениями. Интеграл рационального сплайна не обязательно должен быть рациональным сплайном, следовательно, нет возможности удлинить fnint к рациональным сплайнам. Производная рационального сплайна снова является рациональным сплайном, но один примерно в два раза больше порядка. По этой причине fnder и fndir не коснется рациональных сплайнов. Вместо этого существует команда fntlr для вычисления значения при заданном x всех производных вплоть до заданного порядка данной функции. Если эта функция является рациональной, то необходимый расчет основывается на соображениях, приведенных в предыдущем пункте.
Команда r = rsmak(shape) обеспечивает рациональные сплайны в rBform, которые описывают точно определенные стандартные геометрические формы, как 'circle', 'arc', 'cylinder', 'sphere', 'cone', 'torus'. Команда fncmb(r,trans) может использоваться для применения стандартных преобразований к результирующей фигуре. Например, если trans является столбцом-вектором правой длины, форма будет преобразована этим вектором, в то время как, если trans является подходящей матрицей, подобной вращению, форма будет преобразована этой матрицей.
Команда r = rscvn(p) строит квадратичную rBформу касательно-непрерывной кривой, состоящей из дуг окружности и проходящей через заданную последовательность, p, точек в плоскости.
Специальная рациональная сплайновая форма, называемая NURBS, стала стандартным инструментом в CAGD. NURBS - это, по определению, любой рациональный сплайн, для которого как s, так и w имеют одну и ту же B-форму, причем каждый коэффициент для s содержит явно соответствующий коэффициент для w в качестве фактора:
w=∑iBiv (i)
Нормализованные коэффициенты a (:, i) для числительного сплайна легче использовать в качестве управляющих точек, чем ненормализованные коэффициенты v (i) a (:, i), используемые в rBform. Тем не менее, эта панель инструментов не предоставляет специальной NURBS-формы, а только более общий рациональный сплайн, но в обоих B-форме ( называетсяrBform внутри) и в ppform (называется rpform внутри).
Рациональный сплайн circle использованный ранее, объединен в rsmak по коду, подобному следующему.
x = [1 1 0 -1 -1 -1 0 1 1]; y = [0 1 1 1 0 -1 -1 -1 0]; s45 = 1/sqrt(2); w =[1 s45 1 s45 1 s45 1 s45 1]; circle = rsmak(augknt(0:4,3,2), [w.*x;w.*y;w]);
Обратите внимание на появление сплайна знаменателя в качестве последнего компонента. Также обратите внимание, как коэффициенты знаменательного сплайна отображаются здесь явно как коэффициенты соответствующих коэффициентов числительного сплайна. Нормированная последовательность коэффициентов [x;y] очень просто; он состоит из вершин и средних точек, в правильном порядке, «единичного квадрата». Результирующий управляющий многоугольник является касательным к окружности в местах примыкания четырех квадратичных участков, образующих окружность.
Подробное обсуждение NURBS см. в [G. Farin, NURBS, 2-е изд., AKPeters Ltd, 1999] или [Les Piegl and Wayne Tiller, The NURBS Book, 2-е изд., Springer-Verlag, 1997].