В данном разделе рассматриваются следующие аспекты построения шлица Чебышёва:
Шлиц Чебышёва C = Ct = Ck, t порядка k для узловой последовательности t = (ti: i = 1: n + k) - уникальный элемент Sk, t max-norm 1, который максимально колеблется на интервале [tk.. tn + 1] и положителен около tn + 1. Это означает, что существует уникальная строго увеличивающаяся n-последовательность, так что функция C=Ct∊Sk,t заданная C (starti) = (-1) n-1, all i, имеет max-norm 1 на [tk.. tn + 1]. Из этого следует, что ti1 = tk, tin = tn + 1, и что tii < thei < tk + i, для всех i. На самом деле, ti + 1 ≤ tii ≤ ti + k-1, все i. Это приводит к тому, что предполагается, что последовательность узлов делает такое неравенство возможным, т.е. элементы Sk, t считаются непрерывными.
Короче говоря, чебышёвский сплайн С выглядит так же, как чебышёвский многочлен. Выполняет аналогичные функции. Например, его крайние участки (,, в частности, являются хорошими участками для интерполяции от Sk, t, потому что норма результирующего проектора примерно так мала, как может быть; см. команду панели инструментовchbpnt.
Можно запустить пример Конструирование шлица Чебышева для конструирования C для определенной узловой последовательности t.
Вы имеете дело с кубическими сплайнами, т.е. с порядком
k = 4;
и использовать последовательность разрывов
breaks = [0 1 1.1 3 5 5.5 7 7.1 7.2 8]; lp1 = length(breaks);
и использовать простые внутренние узлы, т.е. использовать последовательность узлов
t = breaks([ones(1,k) 2:(lp1-1) lp1(:,ones(1,k))]); n = length(t)-k;
Обратите внимание на четверной узел на каждом конце. Поскольку k = 4, это делает [0.. 8] = [breaks(1)..breaks(lp1)] интервал [tk.. tn + 1], представляющий интерес, сn = length(t)-k размер результирующего сплайнового пространства Sk, t. Та же последовательность узлов поставлялась бы
t=augknt(breaks,k);
В качестве начальной догадки для
− 1 )/( k − 1)
рекомендуется как хороший выбор сайта интерполяции. Они поставляются
tau=aveknt(t,k);
Постройте график полученного первого приближения к C, т.е. сплайну c, который удовлетворяет c (starti) = (-1) n- i, все i:
b = cumprod(repmat(-1,1,n)); b = b*b(end); c = spapi(t,tau,b); fnplt(c,'-.') grid
Вот получившийся график.
Первое приближение к сплайну Чебышева
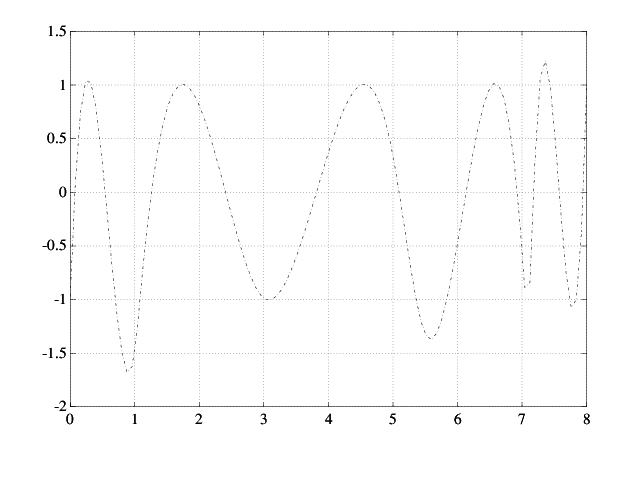
Начиная с этой аппроксимации, вы используете алгоритм Ремеза, чтобы создать последовательность сплайнов, сходящихся к C. Это означает, что вы построите новый, как экстремум вашего текущего аппроксимации c к C и повторите попытку. Вот вся петля.
Вы находите новый интерьер в виде нулей Dc, то есть первой производной c, в несколько шагов. Во-первых, дифференцируйте:
Dc = fnder(c);
Затем возьмите нули управляющего многоугольника Dc в качестве первого предположения для нулей Dc. Для этого необходимо разделить сплайн Dc.
[knots,coefs,np,kp] = fnbrk(Dc,'knots','coefs','n','order');
Управляющий многоугольник имеет вершины (tstar(i),coefs(i)), с tstar усредненные узловые значения для сплайна, aveknt:
tstar = aveknt(knots,kp);
Вот нули результирующего управляющего многоугольника Dc:
npp = (1:np-1); guess = tstar(npp) -coefs(npp).*(diff(tstar)./diff(coefs));
Это уже дает очень хорошее первое предположение для фактических нулей.
Уточните эту оценку для нулей Dc на два шага секущего метода tau и полученные в результате guess как ваши первые приближения. Сначала вычислите Dc в обоих наборах:
sites = tau(ones(4,1),2:n-1); sites(1,:) = guess; values = zeros(4,n-2); values(1:2,:) = reshape(fnval(Dc,sites(1:2,:)),2,n-2);
Теперь подойди к двум шагам секущего метода. Для защиты от деления на ноль установите разность значений функции равной 1 в случае, если она равна нулю. Поскольку ДК строго монотонен рядом с искомыми участками, это безвредно:
for j=2:3
rows = [j,j-1];Dcd=diff(values(rows,:));
Dcd(find(Dcd==0)) = 1;
sites(j+1,:) = sites(j,:) ...
-values(j,:).*(diff(sites(rows,:))./Dcd);
values(j+1,:) = fnval(Dc,sites(j+1,:));
end
Проверка
max(abs(values.')) ans = 4.1176 5.7789 0.4644 0.1178
показывает улучшение.
Теперь примите эти сайты как свои новые tau,
tau = [tau(1) sites(4,:) tau(n)];
и проверьте экстремальные значения вашего текущего приближения там:
extremes = abs(fnval(c, tau));
Различие
max(extremes)-min(extremes) ans = 0.6905
оценка того, насколько вы далеки от общего выравнивания.
Построение нового сплайна, соответствующего новому выбору tau и постройте его поверх старого:
c = spapi(t,tau,b); sites = sort([tau (0:100)*(t(n+1)-t(k))/100]); values = fnval(c,sites); hold on, plot(sites,values)
Следующий код включает сетку и отображает расположение экстремума.
grid on plot( tau(2:end-1), zeros( 1, np-1 ), 'o' ) hold off legend( 'Initial Guess', 'Current Guess', 'Extreme Locations',... 'location', 'NorthEastOutside' );
Ниже приведен результирующий рисунок (легенда не показана).
Более близкий к уровню сплайн
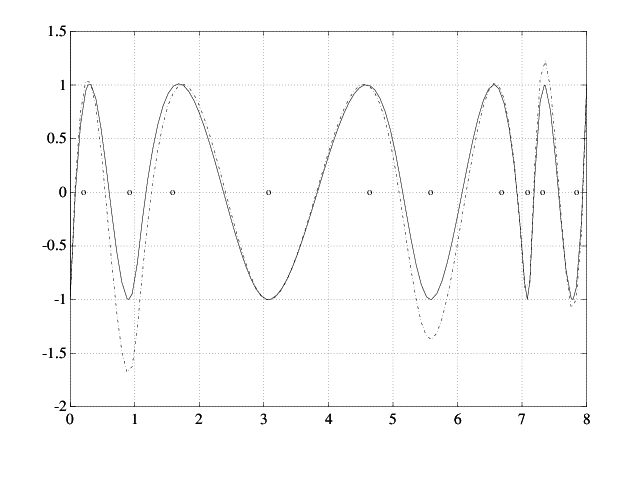
Если это недостаточно близко, можно просто повторить цикл. В этом примере следующая итерация уже производит C с точностью до графики.