Ряд Фурье - это сумма синусоидальных и косинусных функций, описывающая периодический сигнал. Он представлен либо в тригонометрической, либо в экспоненциальной форме. Панель инструментов предоставляет эту тригонометрическую форму серии Фурье
iwx)
где a0 моделирует постоянный (перехватывающий) член в данных и связан с i = 0 косинусным членом, w - основная частота сигнала, n - число членов (гармоник) в ряду, и 1 ≤ n ≤ 8.
Дополнительные сведения о серии Фурье см. в разделе Анализ и фильтрация Фурье.
Откройте приложение «Фитинг кривой», введя cftool. Либо щелкните Фитинг кривой (Curve Fitting) на вкладке Приложения (Apps).
В приложении «Фитинг кривой» выберите данные кривой (данные X и Y или только данные Y по индексу).
Приложение «Фитинг кривой» создает аппроксимацию кривой по умолчанию. Polynomial.
Изменение типа модели с Polynomial кому Fourier.
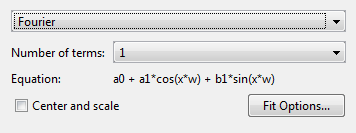
Можно задать следующие параметры:
Выберите количество терминов: 1 кому 8.
Просмотрите на панели Результаты (Results) термины модели, значения коэффициентов и статистику соответствия.
(Необязательно) Нажмите кнопку «Параметры подгонки», чтобы задать начальные значения коэффициентов и ограничения или изменить настройки алгоритма.
Панель инструментов вычисляет оптимизированные начальные точки для моделей серии Фурье на основе текущего набора данных. Можно переопределить начальные точки и указать собственные значения в диалоговом окне «Параметры вписывания».
Дополнительные сведения о параметрах см. в разделах Задание параметров посадки и Оптимизированные начальные точки.
Пример сравнения соответствия библиотеки Фурье с пользовательскими уравнениями см. в разделе Пользовательский нелинейный анализ данных ENSO.
В этом примере показано, как использовать fit для соответствия модели Фурье данным.
Модель библиотеки Фурье является входным аргументом для fit и fittype функции. Укажите тип модели fourier за которым следует число терминов, например, 'fourier1' кому 'fourier8' .
Этот пример соответствует данным El Nino-Southern Solvation (ENSO). Данные ENSO состоят из среднемесячных среднемесячных разниц атмосферного давления между островом Пасхи и Дарвином, Австралия. Эта разница движет торговыми ветрами в южном полушарии.
Данные ENSO являются явно периодическими, что позволяет предположить, что они могут быть описаны серией Фурье. Используйте модели серии Фурье для поиска периодичности.
Подогнать двухсрочную модель Фурье
Загрузите некоторые данные и установите двухсрочную модель Фурье.
load enso; f = fit(month,pressure,'fourier2')
f =
General model Fourier2:
f(x) = a0 + a1*cos(x*w) + b1*sin(x*w) +
a2*cos(2*x*w) + b2*sin(2*x*w)
Coefficients (with 95% confidence bounds):
a0 = 10.63 (10.23, 11.03)
a1 = 2.923 (2.27, 3.576)
b1 = 1.059 (0.01593, 2.101)
a2 = -0.5052 (-1.086, 0.07532)
b2 = 0.2187 (-0.4202, 0.8576)
w = 0.5258 (0.5222, 0.5294)
plot(f,month,pressure)

Доверительные границы на a2 и b2 перекрестный ноль. Для линейных членов нельзя быть уверенным, что эти коэффициенты отличаются от нуля, поэтому они не помогают с посадкой. Это означает, что эта модель двух терминов, вероятно, не лучше, чем модель одного термина.
Период измерения
w term - мера периода. 2*pi/w преобразуется в период в месяцах, поскольку период sin() и cos() является 2*pi .
w = f.w
w = 0.5258
2*pi/w
ans = 11.9497
w это очень близко к 12 месяцам, что указывает на ежегодный период. Наблюдать это выглядит правильно на графике, с пиками примерно 12 месяцев.
Подогнать модель Фурье на восемь сроков
f2 = fit(month,pressure,'fourier8')f2 =
General model Fourier8:
f2(x) =
a0 + a1*cos(x*w) + b1*sin(x*w) +
a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w) +
a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w) +
a6*cos(6*x*w) + b6*sin(6*x*w) + a7*cos(7*x*w) + b7*sin(7*x*w) +
a8*cos(8*x*w) + b8*sin(8*x*w)
Coefficients (with 95% confidence bounds):
a0 = 10.63 (10.28, 10.97)
a1 = 0.5668 (0.07981, 1.054)
b1 = 0.1969 (-0.2929, 0.6867)
a2 = -1.203 (-1.69, -0.7161)
b2 = -0.8087 (-1.311, -0.3065)
a3 = 0.9321 (0.4277, 1.436)
b3 = 0.7602 (0.2587, 1.262)
a4 = -0.6653 (-1.152, -0.1788)
b4 = -0.2038 (-0.703, 0.2954)
a5 = -0.02919 (-0.5158, 0.4575)
b5 = -0.3701 (-0.8594, 0.1192)
a6 = -0.04856 (-0.5482, 0.4511)
b6 = -0.1368 (-0.6317, 0.3581)
a7 = 2.811 (2.174, 3.449)
b7 = 1.334 (0.3686, 2.3)
a8 = 0.07979 (-0.4329, 0.5925)
b8 = -0.1076 (-0.6037, 0.3885)
w = 0.07527 (0.07476, 0.07578)
plot(f2,month,pressure)

Период измерения
w = f2.w
w = 0.0753
(2*pi)/w
ans = 83.4736
С помощью f2 модель, период w составляет примерно 7 лет.
Изучить условия
Ищите коэффициенты с наибольшей величиной, чтобы найти наиболее важные термины.
a7 и b7 являются самыми крупными. Посмотрите на a7 член в уравнении модели: a7*cos(7*x*w). 7*w = = 7/7 = 1 год цикла .a7 и b7 указать, что годовой цикл является самым сильным.
Аналогично, a1 и b1 термины дают 7/1, указывая семилетний цикл.
a2 и b2 термины представляют собой 3,5-летний цикл (7/2). Это сильнее, чем 7-летний цикл, потому что a2 и b2 коэффициенты имеют большую величину, чем a1 и b1.
a3 и b3 достаточно строгие термины, указывающие на цикл 7/3 или 2,3 года.
Меньшие термины менее важны для подгонки, такие как a6, b6, a5, и b5.
Обычно потепление Эль-Нино происходит с нерегулярными интервалами от двух до семи лет и длится от девяти месяцев до двух лет. Средняя продолжительность периода составляет пять лет. Результаты модели отражают некоторые из этих периодов.
Задать начальные точки
Панель инструментов вычисляет оптимизированные начальные точки для посадок Фурье на основе текущего набора данных. Модели рядов Фурье особенно чувствительны к начальным точкам, и оптимизированные значения могут быть точными только для нескольких членов в связанных уравнениях. Можно переопределить начальные точки и задать собственные значения.
После изучения терминов и графиков, похоже, что 4-летний цикл может присутствовать. Попробуйте подтвердить это, установив w. Получить значение для w, где 8 лет = 96 месяцев.
w = (2*pi)/96
w = 0.0654
Найдите порядок записей для коэффициентов в модели ('f2') с помощью coeffnames функция.
coeffnames(f2)
ans = 18x1 cell
{'a0'}
{'a1'}
{'b1'}
{'a2'}
{'b2'}
{'a3'}
{'b3'}
{'a4'}
{'b4'}
{'a5'}
{'b5'}
{'a6'}
{'b6'}
{'a7'}
{'b7'}
{'a8'}
{'b8'}
{'w' }
Получение текущих значений коэффициентов.
coeffs = coeffvalues(f2)
coeffs = 1×18
10.6261 0.5668 0.1969 -1.2031 -0.8087 0.9321 0.7602 -0.6653 -0.2038 -0.0292 -0.3701 -0.0486 -0.1368 2.8112 1.3344 0.0798 -0.1076 0.0753
Установите последний коэффициент, w, до 0,065.
coeffs(:,18) = w
coeffs = 1×18
10.6261 0.5668 0.1969 -1.2031 -0.8087 0.9321 0.7602 -0.6653 -0.2038 -0.0292 -0.3701 -0.0486 -0.1368 2.8112 1.3344 0.0798 -0.1076 0.0654
Задайте начальные точки для коэффициентов, используя новое значение для w.
f3 = fit(month,pressure,'fourier8', 'StartPoint', coeffs);
Постройте график, чтобы увидеть, что новое значение для w в f3 не обеспечивает лучшего соответствия, чем f2 .
plot(f3,month,pressure) hold on plot(f2, 'b') hold off legend( 'Data', 'f3', 'f2')

Найти параметры посадки Фурье
Поиск доступных параметров подгонки с помощью fitoptions(modelname), где modelname - тип модели fourier за которым следует число терминов, например, 'fourier1' кому 'fourier8' .
fitoptions('fourier8')ans =
Normalize: 'off'
Exclude: []
Weights: []
Method: 'NonlinearLeastSquares'
Robust: 'Off'
StartPoint: [1x0 double]
Lower: [1x0 double]
Upper: [1x0 double]
Algorithm: 'Trust-Region'
DiffMinChange: 1.0000e-08
DiffMaxChange: 0.1000
Display: 'Notify'
MaxFunEvals: 600
MaxIter: 400
TolFun: 1.0000e-06
TolX: 1.0000e-06
Если требуется изменить параметры подгонки, такие как начальные значения коэффициентов и границы ограничений, соответствующие данным, или изменить настройки алгоритма, см. параметры для параметра «Нелинейные квадраты» на вкладке fitoptions справочная страница.
fit | fitoptions | fittype