Кусочно-биарковая эрмитовая интерполяция
c = rscvn(p,u)
c = rscvn(p)
c = rscvn(p,u) возвращает плоскую кусочно-двойную кривую (в квадратичной rBform), которая проходит по порядку через заданные точки p(:,j) и строится следующим образом (см. Строительство Biarc). Между любыми двумя различными точками p(:,j) и p(:,j+1), кривая обычно состоит из двух дуг окружности (включая прямолинейные сегменты), которые соединяются с касательной непрерывностью, при этом первая дуга начинается с p(:,j) и нормально там, чтобы u(:,j), и вторая дуга заканчивается на p(:,j+1) и нормально там, чтобы u(:,j+1)и с двумя дугами, записанными как одна, когда это возможно. Таким образом, кривая является касательно-непрерывной везде, за исключением, возможно, в повторяющихся точках, где кривая может иметь угол, или когда угол, образованный двумя сегментами, заканчивающимися на p(:,j), необычно мало, и в этом случае кривая может иметь cusp в этой точке.
p должен быть вещественной матрицей, с двумя строками и по крайней мере двумя столбцами, и любой столбец должен отличаться по крайней мере от одного из соседних столбцов.
u должна быть вещественной матрицей с двумя строками, с тем же количеством столбцов, что и p (для двух исключений см. ниже) и не может иметь нулевого столбца.
c = rscvn(p) выбирает нормали следующим образом. Для j=2:end-1, u(:,j) - среднее значение нормализованных, поворачивающихся вправо нормалей к векторам p(:,j)-p(:,j-1) и p(:,j+1)-p(:,j). Если p(:,1)==p(:,end), то оба конечных нормаля выбираются как среднее из нормалей к p(:,2)-p(:,1) и p(:,end)-p(:,end-1) таким образом предотвращается угол в результирующей замкнутой кривой. В противном случае концевые нормали выбираются таким образом, что имеется только одна дуга над первым и последним сегментом (не-узловое концевое условие).
rscvn(p,u), с u имея ровно две колонны, также выбирает внутренние нормали, как для случая, когда u отсутствует, но использует два столбца u в качестве конечных нормалей.
Пример 1. Следующий код создает описание круга, используя только четыре части. За исключением другого масштабирования узловой последовательности, оно является тем же описанием, которое предоставляется rsmak('circle',1,[1;1]).
p = [1 0 -1 0 1; 0 1 0 -1 0]; c = rscvn([p(1,:)+1;p(2,:)+1],p);
Одна и та же окружность, но с использованием только двух частей, обеспечивается
c2 = rscvn([0,2,0; 1,1,1]);
Пример 2. Следующий код отображает две буквы. Обратите внимание, что вторая буква является результатом интерполяции всего до четырех точек. Обратите внимание также на использование перевода при печати второй буквы.
p = [-1 .8 -1 1 -1 -1 -1; 3 1.75 .5 -1.25 -3 -3 3]; i = eye(2); u = i(:,[2 1 2 1 2 1 1]); B = rscvn(p,u); S = rscvn([1 -1 1 -1; 2.5 2.5 -2.5 -2.5]); fnplt(B), hold on, fnplt(fncmb(S,[3;0])), hold off axis equal, axis off
Две буквы, состоящие из дуг окружности

Пример 3. Следующий код генерирует конструкцию Biarc, используемую в приведенном ниже описании конструкции biarc, используемой здесь. Обратите внимание на использование fntlr найти касательную к биарке в начале, в точке соединения двух дуг и в конце.
p = [0 1;0 0]; u = [.5 -.1;-.25 .5]; plot(p(1,:),p(2,:),'k'), hold on biarc = rscvn(p,u); breaks = fnbrk(biarc,'b'); fnplt(biarc,breaks(1:2),'b',3), fnplt(biarc,breaks(2:3),'r',3) vd = fntlr(biarc,2,breaks); quiver(vd(1,:),vd(2,:),vd(4,:),-vd(3,:)), hold off
Строительство Биарка
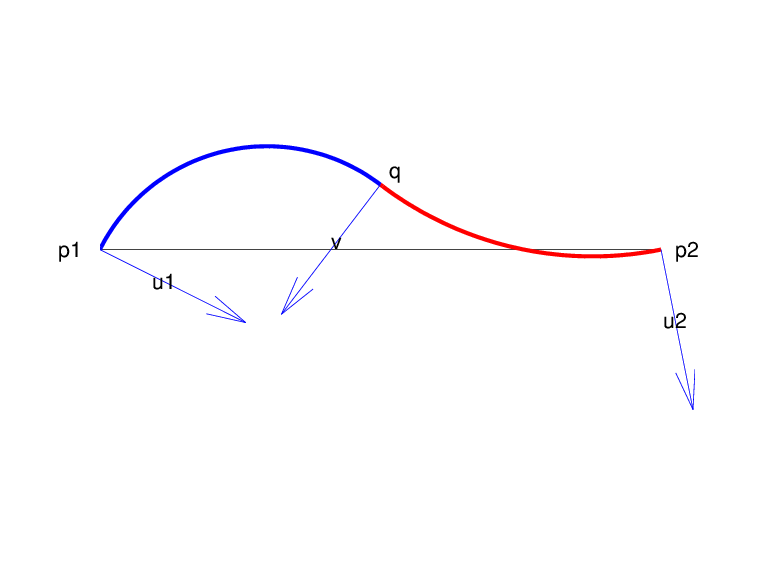
Учитывая два различных момента, p1 и p2, в плоскости и, соответственно, два ненулевых вектора, u1 и u2, существует однопараметрическое семейство биаркс (т.е. кривая, состоящая из двух дуг с общей касательной в их соединении), начиная с p1 и нормально там, чтобы u1 и заканчивающиеся на p2 и нормально там, чтобы u2. Один из способов параметризовать это семейство биаркс по нормали, v, в точке q при котором соединяются две дуги. С ненулевым значением v выбрано, то есть ровно один выбор qзатем определяют всю биарку. В конструкции, используемой в rscvn, v выбирается в качестве отражения, поперек перпендикулярного сегменту от p1 кому p2, среднего значения векторов u1 и u2, - после того, как оба вектора были настолько нормализованы, что их длина равна 1 и оба они указывают справа от сегмента от p1 кому p2. Этот выбор для v представляется естественным в двух стандартных случаях: i) u2 является отражением u1 поперек перпендикулярно сегменту от p1 кому p2; (ii) u1 и u2 параллельны. Этот выбор v проверяется Biarks как функция левого нормаля, которая показывает результирующие biarks, когда p1, p2, и u2 = [.809;.588]сохраняются фиксированными и только нормальными в p1 допускается изменение.
Биарки как функция левого нормаля

Но невозможно, чтобы интерполяционная биарка зависела непрерывно на всех четырех данных, p1, p2, u1, u2. В качестве нормальных направлений должен быть разрыв, u1 и u2, пройти через направление от p1 кому p2. Это показано в Biarks как функция одной конечной точки, которая показывает biarks в одной точке, p1 = [0;0]и две нормали, u1 = [1;1] и u2 = [1;-1], удерживаются фиксированными и только другой точкой, p2, движется, по кругу вокруг p1.
Биарксы как функция одной конечной точки
