Чтобы увидеть примеры использования сетей NARX, применяемых в форме с разомкнутым контуром, форме с замкнутым контуром и многоступенчатом прогнозировании с разомкнутым/замкнутым контуром, см. Многоступенчатое предсказание нейронной сети.
Все конкретные динамические сети, обсуждавшиеся до сих пор, были либо сфокусированными сетями, причем динамика была только на уровне ввода, либо сетями прямой связи. Нелинейная авторегрессионная сеть с экзогенными входами (NARX) представляет собой повторяющуюся динамическую сеть, с соединениями обратной связи, охватывающими несколько уровней сети. Модель NARX основана на линейной модели ARX, которая обычно используется в моделировании временных рядов.
Определяющее уравнение для модели NARX:
1), u (t − 2),..., u (t − nu))
где следующее значение зависимого выходного сигнала y (t) регрессируется по предыдущим значениям выходного сигнала и предыдущим значениям независимого (экзогенного) входного сигнала. Можно реализовать модель NARX, используя нейронную сеть прямой связи для аппроксимации функции f. Ниже показана диаграмма результирующей сети, где для аппроксимации используется двухуровневая сеть прямой связи. Эта реализация также позволяет использовать векторную модель ARX, где входные и выходные данные могут быть многомерными.
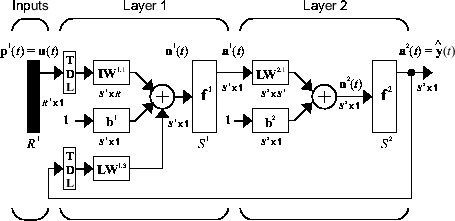
Существует множество приложений для сети NARX. Он может использоваться в качестве предиктора для прогнозирования следующего значения входного сигнала. Он также может использоваться для нелинейной фильтрации, в которой целевой выход является безшумной версией входного сигнала. Использование сети NARX показано в другом важном приложении, моделировании нелинейных динамических систем.
Перед показом обучения сети NARX необходимо пояснить важную конфигурацию, полезную для обучения. Вывод сети NARX можно рассматривать как оценку вывода какой-либо нелинейной динамической системы, которую вы пытаетесь смоделировать. Выходной сигнал подается обратно на вход нейронной сети прямой связи как часть стандартной архитектуры NARX, как показано на левом рисунке ниже. Поскольку истинный выход доступен во время обучения сети, можно создать последовательную параллельную архитектуру (см. [NaPa91]), в которой истинный выход используется вместо обратной передачи расчетного выхода, как показано на правом рисунке ниже. Это имеет два преимущества. Первый заключается в том, что вход в сеть прямой связи является более точным. Вторая заключается в том, что результирующая сеть имеет архитектуру, ориентированную исключительно на обратную связь, и статическое обратное распространение может использоваться для обучения.
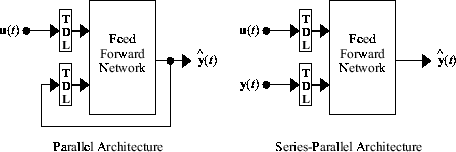
Ниже показано использование последовательной параллельной архитектуры для обучения сети NARX моделированию динамической системы.
Примером сети NARX является система магнитной левитации, описанная в разделе Использование блока контроллера NARMA-L2. Нижний график на следующем рисунке показывает напряжение, приложенное к электромагниту, а верхний график показывает положение постоянного магнита. Данные собирали с интервалом выборки 0,01 секунды для формирования двух временных рядов.
Целью является разработка модели NARX для этой системы магнитной левитации.
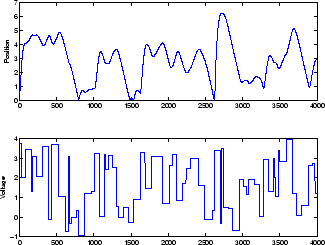
Сначала загрузите данные обучения. Используйте линии задержки с двумя задержками как для входа, так и для выхода, поэтому обучение начинается с третьей точки данных. Имеется два входа в последовательную параллельную сеть, последовательность u (t) и последовательность y (t).
load magdata
y = con2seq(y);
u = con2seq(u);
Создание последовательной параллельной сети NARX с помощью функции narxnet. Используйте 10 нейронов в скрытом слое и используйте trainlm для функции обучения, а затем подготовить данные с помощью preparets:
d1 = [1:2];
d2 = [1:2];
narx_net = narxnet(d1,d2,10);
narx_net.divideFcn = '';
narx_net.trainParam.min_grad = 1e-10;
[p,Pi,Ai,t] = preparets(narx_net,u,{},y);
(Обратите внимание, что y последовательность считается сигналом обратной связи, который является входом, который также является выходом (целью). Позднее, при закрытии контура, соответствующий выход будет подключен к соответствующему входу.) Теперь вы готовы тренировать сеть.
narx_net = train(narx_net,p,t,Pi);
Теперь можно моделировать сетевой график и выводить на график результирующие ошибки для последовательного параллельного внедрения.
yp = sim(narx_net,p,Pi); e = cell2mat(yp)-cell2mat(t); plot(e)

Видно, что ошибки очень малы. Однако из-за последовательной параллельной конфигурации это ошибки только для предсказания на один шаг вперед. Более строгим тестом было бы переупорядочить сеть в исходную параллельную форму (замкнутый цикл) и затем выполнить итерационное предсказание в течение многих временных шагов. Теперь показана параллельная операция.
Существует функция панели инструментов (closeloop) для преобразования NARX (и других) сетей из последовательной параллельной конфигурации (разомкнутая петля), которая полезна для обучения, в параллельную конфигурацию (замкнутая петля), которая полезна для многошагового прогнозирования. Следующая команда иллюстрирует преобразование только что обученной сети в параллельную форму:
narx_net_closed = closeloop(narx_net);
Для просмотра различий между двумя сетями можно использовать команду view:
view(narx_net)

view(narx_net_closed)

Все обучение выполняется в открытом цикле (также называемом последовательно-параллельной архитектурой), включая этапы проверки и тестирования. Типичный рабочий процесс состоит в том, чтобы полностью создать сеть в разомкнутом цикле, и только после обучения (которое включает в себя этапы проверки и тестирования) она преобразуется в замкнутый цикл для многоступенчатого прогнозирования. Аналогично, R значения в GUI вычисляются на основе результатов обучения с разомкнутым контуром.
Теперь можно использовать конфигурацию с замкнутым контуром (параллельную) для выполнения итерационного прогнозирования 900 временных шагов. В этой сети необходимо загрузить два начальных входа и два начальных выхода в качестве начальных условий. Вы можете использовать preparets для подготовки данных. Она будет использовать сетевую структуру для определения того, как разделить и соответствующим образом сдвинуть данные.
y1 = y(1700:2600);
u1 = u(1700:2600);
[p1,Pi1,Ai1,t1] = preparets(narx_net_closed,u1,{},y1);
yp1 = narx_net_closed(p1,Pi1,Ai1);
TS = size(t1,2);
plot(1:TS,cell2mat(t1),'b',1:TS,cell2mat(yp1),'r')

Рисунок иллюстрирует итерационное предсказание. Синяя линия - это фактическое положение магнита, а красная - это положение, предсказанное нейронной сетью NARX. Даже если сеть предсказывает 900 шагов вперед, предсказание является очень точным.
Для того чтобы параллельный ответ (итерируемое предсказание) был точным, важно, чтобы сеть была обучена так, чтобы ошибки в последовательной параллельной конфигурации (одношаговое предсказание) были очень малы.
Можно также создать параллельную (замкнутую) сеть NARX, используя narxnet команда с четвертым входным аргументом, установленным на 'closed'и обучить эту сеть напрямую. Как правило, обучение занимает больше времени, и результирующая производительность не так хороша, как при последовательном параллельном обучении.
Каждый раз, когда нейронная сеть обучается, может привести к различному решению из-за различных начальных значений веса и смещения и различных разделов данных в обучающих, валидационных и тестовых наборах. В результате различные нейронные сети, обученные одной и той же проблеме, могут давать разные выходы для одного и того же входа. Чтобы была найдена нейронная сеть хорошей точности, переучивайтесь несколько раз.
Существует несколько других способов улучшения исходных решений, если требуется более высокая точность. Дополнительные сведения см. в разделе Улучшение неглубокого обобщения нейронных сетей и предотвращение переоборудования.
Пример маглева показал, как моделировать временной ряд с одним внешним входным значением во времени. Но сеть NARX будет работать для проблем с несколькими внешними элементами ввода и предсказывать серии с несколькими элементами. В этих случаях входной и целевой элементы состоят из массивов ячеек строк, представляющих время, но каждый элемент ячейки является N-по-1 вектору для N элементы входного или целевого сигнала.
Например, вот набор данных, который состоит из 2-элементных внешних переменных, предсказывающих 1-элементный ряд.
[X,T] = ph_dataset;
Внешние входы X форматируют как массив ячеек строки из 2-элементных векторов, причем каждый вектор представляет собой поток кислоты и основного раствора. Целевые показатели представляют результирующий рН раствора с течением времени.
Вы можете переформатировать свои собственные многоэлементные серийные данные из матричной формы в нейронную сетевую форму временных рядов с помощью функции con2seq.
Процесс обучения сети проходит так же, как и выше для проблемы маглева.
net = narxnet(10);
[x,xi,ai,t] = preparets(net,X,{},T);
net = train(net,x,t,xi,ai);
y = net(x,xi,ai);
e = gsubtract(t,y); Чтобы увидеть примеры использования сетей NARX, применяемых в форме с разомкнутым контуром, форме с замкнутым контуром и многоступенчатом прогнозировании с разомкнутым/замкнутым контуром, см. Многоступенчатое предсказание нейронной сети.