Динамические сети можно разделить на две категории: те, которые имеют только прямые соединения, и те, которые имеют обратные или повторяющиеся соединения. Чтобы понять различия между статическими, динамическими и повторяющимися сетями, создайте некоторые сети и посмотрите, как они реагируют на последовательность ввода. (Во-первых, можно просмотреть моделирование с последовательными входами в динамической сети.)
Следующие команды создают последовательность импульсного ввода и строят ее график:
p = {0 0 1 1 1 1 0 0 0 0 0 0};
stem(cell2mat(p))

Теперь создайте статическую сеть и найдите ответ сети на последовательность импульсов. Следующие команды создают простую линейную сеть с одним слоем, одним нейроном, без смещения и весом 2:
net = linearlayer;
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.IW{1,1} = 2;
view(net)

Теперь можно смоделировать сетевой отклик на импульсный вход и построить его график:
a = net(p); stem(cell2mat(a))

Следует отметить, что реакция статической сети длится так же долго, как и входной импульс. Отклик статической сети в любой момент времени зависит только от значения входной последовательности в тот же момент времени.
Теперь создайте динамическую сеть, но не имеющую никаких соединений обратной связи (непериодическую сеть). Можно использовать ту же сеть, что и при моделировании с параллельными входами в динамической сети, которая представляла собой линейную сеть с резьбовой линией задержки на входе:
net = linearlayer([0 1]);
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.IW{1,1} = [1 1];
view(net)

Можно снова смоделировать сетевой отклик на импульсный вход и построить его график:
a = net(p); stem(cell2mat(a))

Отклик динамической сети длится дольше, чем входной импульс. Динамическая сеть имеет память. Его отклик в любой данный момент времени зависит не только от текущего входа, но и от истории входной последовательности. Если сеть не имеет каких-либо соединений обратной связи, то только конечный объем истории повлияет на ответ. На этом рисунке видно, что реакция на импульс длится один временной шаг, превышающий длительность импульса. Это происходит потому, что линия задержки на входе имеет максимальную задержку 1.
Рассмотрим простую рекуррентно-динамическую сеть, показанную на следующем рисунке.
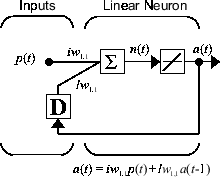
Можно создать сеть, просмотреть ее и смоделировать с помощью следующих команд. narxnet команда обсуждается в серии нейронных сетей обратной связи NARX.
net = narxnet(0,1,[],'closed');
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.LW{1} = .5;
net.IW{1} = 1;
view(net)

Следующие команды отображают сетевой ответ.
a = net(p); stem(cell2mat(a))

Обратите внимание, что повторяющиеся динамические сети обычно имеют более длительный отклик, чем динамические сети. Для линейных сетей динамические сети с прямой связью называются конечными импульсными характеристиками (КИХ), потому что отклик на импульсный вход станет нулевым после конечного количества времени. Линейные рекуррентно-динамические сети называются бесконечной импульсной характеристикой (БИХ), потому что отклик на импульс может затухать до нуля (для стабильной сети), но он никогда не станет точно равным нулю. Импульсный отклик для нелинейной сети не может быть определен, но идеи конечных и бесконечных откликов действительно переносятся.
Динамические сети, как правило, более мощные, чем статические (хотя и несколько более сложные в обучении). Поскольку динамические сети имеют память, их можно обучить изучению последовательных или изменяющихся во времени шаблонов. Это имеет применение в таких разрозненных областях, как прогнозирование на финансовых рынках [RoJa96], выравнивание каналов в системах связи [FeTs03], обнаружение фаз в энергосистемах [KaGr96], сортировка [JaRa04], обнаружение неисправностей [ChDa99], распознавание речи [Robin94] и даже предсказание структуры белка в генетике [GiPr В [MeJa00] можно ознакомиться со многими другими динамическими сетевыми приложениями.
Одно из основных применений динамических нейронных сетей - в системах управления. Это приложение подробно обсуждается в Neural Network Control Systems. Динамические сети также хорошо подходят для фильтрации. Вы увидите использование некоторых линейных динамических сетей для фильтрации в, и некоторые из этих идей расширены в этом разделе, используя нелинейные динамические сети.
Программное обеспечение Deep Learning Toolbox™ предназначено для обучения класса сетей под названием Многоуровневая цифровая динамическая сеть (LDDN). Любая сеть, которая может быть организована в виде LDDN, может быть обучена с помощью панели инструментов. Ниже приведено основное описание LDDN.
Каждый уровень в LDDN состоит из следующих частей:
Набор весовых матриц, приходящих в этот слой (которые могут соединяться из других слоев или из внешних входов), соответствующее правило весовых функций, используемое для объединения весовой матрицы с ее входом (обычно стандартное умножение матрицы, dotprod) и связанной линии задержки с отводом
Вектор смещения
Правило результирующей входной функции, которое используется для объединения выходов различных весовых функций со смещением для создания результирующего входного сигнала (обычно суммирующий переход, netprod)
Передаточная функция
Сеть имеет входы, которые соединены со специальными весами, называемыми входными весами, и обозначаются IWi, j (net.IW{i,j} в коде), где j обозначает номер входного вектора, который входит в вес, и i обозначает номер слоя, с которым связан вес. Веса, соединяющие один слой с другим, называются весами слоев и обозначаются как LWi, j (net.LW{i,j} в коде), где j обозначает номер слоя, входящего в вес, а i обозначает номер слоя на выходе веса.
На следующем рисунке показан пример трехуровневого LDDN. Первый слой имеет три связанных с ним веса: один входной вес, вес слоя от слоя 1 и вес слоя от слоя 3. Веса двух слоев имеют связанные с ними линии задержки с отводами.
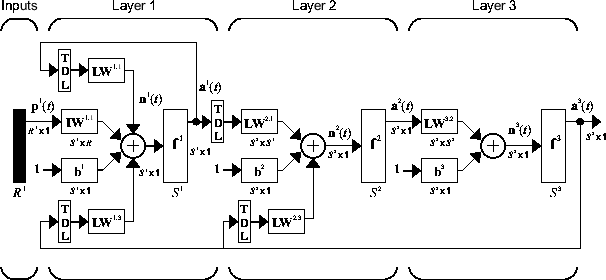
Программное обеспечение Deep Learning Toolbox может использоваться для обучения любого LDDN, если функции веса, функции чистого ввода и функции переноса имеют производные. Большинство известных динамических сетевых архитектур могут быть представлены в виде LDDN. В оставшейся части этого раздела вы увидите, как использовать некоторые простые команды для создания и обучения нескольких очень мощных динамических сетей. Другие сети LDDN, не описанные в этом разделе, могут быть созданы с помощью общей команды network, как описано в разделе Определение неглубоких архитектур нейронных сетей.
Динамические сети обучаются программному обеспечению Deep Learning Toolbox с использованием тех же алгоритмов на основе градиентов, которые были описаны в многоуровневых неглубоких нейронных сетях и обучении обратному распространению. Можно выбрать любую из функций обучения, представленных в этом разделе. Примеры приведены в следующих разделах.
Хотя динамические сети могут быть обучены с использованием тех же алгоритмов на основе градиентов, которые используются для статических сетей, производительность алгоритмов в динамических сетях может быть совершенно иной, и градиент должен быть вычислен более сложным способом. Рассмотрим снова простую повторяющуюся сеть, показанную на этом рисунке.

Веса имеют два различных эффекта на выходе сети. Первый - это прямой эффект, поскольку изменение веса вызывает немедленное изменение выходного сигнала на текущем временном шаге. (Этот первый эффект может быть вычислен с использованием стандартного обратного распространения.) Второй - косвенный эффект, поскольку некоторые входы в слой, такие как a (t − 1), также являются функциями весов. Чтобы учесть этот косвенный эффект, необходимо использовать динамическое обратное распространение для вычисления градиентов, что является более интенсивным вычислением. (См. разделы [DeHa01a], [DeHa01b] и [DeHa07].) Ожидайте, что динамическое обратное распространение займет больше времени для обучения, отчасти по этой причине. Кроме того, поверхности ошибок для динамических сетей могут быть более сложными, чем для статических сетей. Обучение, скорее всего, окажется в ловушке в местных минимумах. Это говорит о том, что для достижения оптимального результата может потребоваться несколько раз обучить сеть. Для получения дополнительной информации по обучению динамическим сетям см. [DHH01] и [HDH09].
В остальных разделах этого раздела показано, как создавать, обучать и применять определенные динамические сети к проблемам моделирования, обнаружения и прогнозирования. Некоторые сети требуют динамического обратного распространения для вычисления градиентов, а другие - нет. Пользователю не нужно решать, требуется ли динамическое обратное распространение. Это определяется автоматически программным обеспечением, которое также решает оптимальную форму динамического обратного распространения. Необходимо просто создать сеть и затем вызвать стандарт. train команда.