Документация

Нейронные сети поезда с весами ошибок

В функции производительности среднеквадратичной ошибки по умолчанию (см. раздел Подготовка и применение многослойных неглубоких нейронных сетей) каждая квадратичная ошибка вносит одинаковую сумму в функцию производительности следующим образом:

Однако панель инструментов позволяет взвешивать каждую ошибку в квадрате по отдельности следующим образом:

Объект взвешивания ошибок должен иметь те же измерения, что и целевые данные. Таким образом, ошибки могут быть взвешены в соответствии с шагом времени, номером выборки, номером сигнала или номером элемента. Ниже приведен пример взвешивания ошибок в конце временной последовательности в большей степени, чем ошибок в начале временной последовательности. Объект взвешивания ошибок передается в качестве последнего аргумента в вызове train.

y = laser_dataset;
y = y(1:600);
ind = 1:600;
ew = 0.99.^(600-ind);
figure
plot(ew)

ew = con2seq(ew);
ftdnn_net = timedelaynet([1:8],10);
ftdnn_net.trainParam.epochs = 1000;
ftdnn_net.divideFcn = '';
[p,Pi,Ai,t,ew1] = preparets(ftdnn_net,y,y,{},ew);
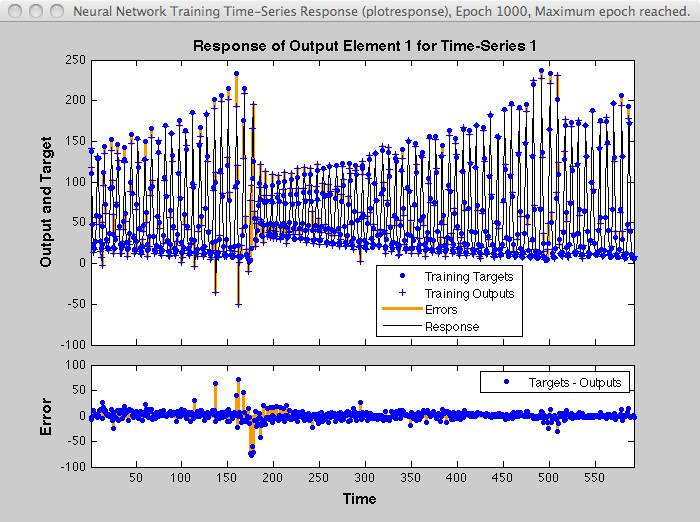
[ftdnn_net1,tr] = train(ftdnn_net,p,t,Pi,Ai,ew1);

На рисунке показано взвешивание ошибок для этого примера. В тренировочных данных имеется 600 временных шагов, и ошибки взвешиваются экспоненциально, причем последняя квадратичная ошибка имеет вес 1, а квадратическая ошибка на первом временном этапе имеет вес 0,0024.

Ответ обученной сети показан на следующем рисунке. Если сравнить этот отклик с откликом сети, которая была обучена без экспоненциального взвешивания по квадратичным ошибкам, как показано в Neural Networks Design Time Series Time-Delay, можно увидеть, что ошибки с опозданием в последовательности меньше, чем ошибки ранее в последовательности. Ошибки, возникшие позже, меньше, поскольку они внесли больший вклад в взвешенный индекс производительности, чем предыдущие ошибки.