Совет
Для обучения сети глубокого обучения используйте trainNetwork.
В этом разделе представлена часть типичного многоуровневого неглубокого сетевого рабочего процесса. Дополнительные сведения и другие шаги см. в разделе Многоуровневые неглубокие нейронные сети и обучение обратному распространению.
При инициализации весов и отклонений сети сеть готова к обучению. Многоуровневая сеть прямой связи может быть обучена функциональному приближению (нелинейной регрессии) или распознаванию образов. Процесс обучения требует набора примеров правильного поведения сети - сетевые входыp и целевые результаты t.
Процесс обучения нейронной сети включает в себя настройку значений весов и смещений сети для оптимизации производительности сети, определяемой функцией производительности сети. net.performFcn. Функция производительности по умолчанию для сетей прямой связи - среднеквадратическая ошибка mse- средняя квадратичная ошибка между выходами сетиa и целевые результаты t. Он определяется следующим образом:
ai) 2
(Отдельные ошибки в квадрате также могут быть взвешены. См. Нейронные сети поездов с весами ошибок.) Существует два различных способа реализации обучения: инкрементный режим и пакетный режим. В режиме приращения градиент вычисляется, и веса обновляются после того, как каждый ввод применяется к сети. В пакетном режиме все входные данные в обучающем наборе применяются к сети до обновления весовых коэффициентов. В этом разделе описывается обучение в пакетном режиме с помощью train команда. Дополнительное обучение с помощью adapt команда рассматривается в пошаговом обучении с адаптацией. Для большинства проблем при использовании программного обеспечения Deep Learning Toolbox™ пакетное обучение происходит значительно быстрее и приводит к меньшим ошибкам, чем инкрементное обучение.
Для обучения многоуровневым сетям прямой связи можно использовать любой стандартный алгоритм численной оптимизации для оптимизации функции производительности, но есть несколько ключевых, которые показали отличную производительность для обучения нейронной сети. Эти методы оптимизации используют либо градиент производительности сети по отношению к весам сети, либо якобиан ошибок сети по отношению к весам.
Градиент и якобиан вычисляются с использованием методики, называемой алгоритмом обратного распространения, который включает в себя выполнение вычислений назад через сеть. Вычисление обратного распространения производится с использованием цепного правила исчисления и описывается в главах 11 (для градиента) и 12 (для якобиана) [HDB96].
В качестве иллюстрации того, как работает обучение, рассмотрим простейший алгоритм оптимизации - градиентный спуск. Он обновляет веса сети и смещения в направлении, в котором функция производительности уменьшается наиболее быстро, отрицательный от градиента. Одну итерацию этого алгоритма можно записать как
− αkgk
где xk - вектор текущих весов и смещений, gk - текущий градиент, а αk - скорость обучения. Это уравнение итерируется до тех пор, пока сеть не сойдется.
Список алгоритмов обучения, доступных в программном обеспечении Deep Learning Toolbox и использующих методы на основе градиента или якобиана, представлен в следующей таблице.
Подробное описание нескольких из этих техник см. также Hagan, M.T., H.B. Demuth, и M.H. Beale, Neural Network Design, Boston, MA: PWS Publishing, 1996, главы 11 и 12.
Функция | Алгоритм |
|---|---|
Левенберг-Марквардт | |
Байесовская регуляризация | |
BFGS Квази-Ньютон | |
Упругое обратное распространение | |
Масштабированный сопряженный градиент | |
Сопряжение градиента с перезапуском Пауэлла/Била | |
Сопряженный градиент Флетчера-Пауэлла | |
Сопряженный градиент Полака-Рибьера | |
Одношаговый секант | |
Градиентный спуск переменной скорости обучения | |
Градиентный спуск с импульсом | |
Градиентный спуск |
Самая быстрая функция обучения, как правило, trainlm, и это функция обучения по умолчанию для feedforwardnet. Метод квази-Ньютона, trainbfg, также довольно быстро. Оба эти метода имеют тенденцию быть менее эффективными для больших сетей (с тысячами весов), так как они требуют больше памяти и больше времени вычислений для этих случаев. Также, trainlm лучше выполняет задачи функциональной подгонки (нелинейной регрессии), чем задачи распознавания образов.
При обучении больших сетей и при обучении сетей распознавания образов trainscg и trainrp это хороший выбор. Их требования к памяти относительно невелики, и тем не менее они намного быстрее, чем стандартные алгоритмы градиентного спуска.
См. раздел Выбор многоуровневой функции обучения нейронной сети для полного сравнения характеристик алгоритмов обучения, показанных в таблице выше.
В качестве примечания к терминологии термин «обратное распространение» иногда используется для обозначения конкретно алгоритма градиентного спуска, когда применяется к обучению нейронной сети. Эта терминология здесь не используется, так как процесс вычисления градиента и якобиана путем выполнения вычислений назад через сеть применяется во всех перечисленных выше обучающих функциях. Более ясно использовать имя используемого алгоритма оптимизации, а не использовать только термин backpropagation.
Кроме того, многослойную сеть иногда называют сетью обратного распространения. Однако метод обратного распространения, который используется для вычисления градиентов и якобианов в многослойной сети, также может быть применен ко многим различным сетевым архитектурам. Фактически градиенты и якобинцы для любой сети, которая имеет дифференцированные передаточные функции, весовые функции и функции чистого ввода, могут быть вычислены с помощью программного обеспечения Deep Learning Toolbox через процесс обратного распространения. Можно даже создать собственные пользовательские сети и затем обучить их с помощью любой из функций обучения, приведенных в таблице выше. Градиенты и якобинцы будут вычисляться автоматически.
Для иллюстрации процесса обучения выполните следующие команды:
load bodyfat_dataset
net = feedforwardnet(20);
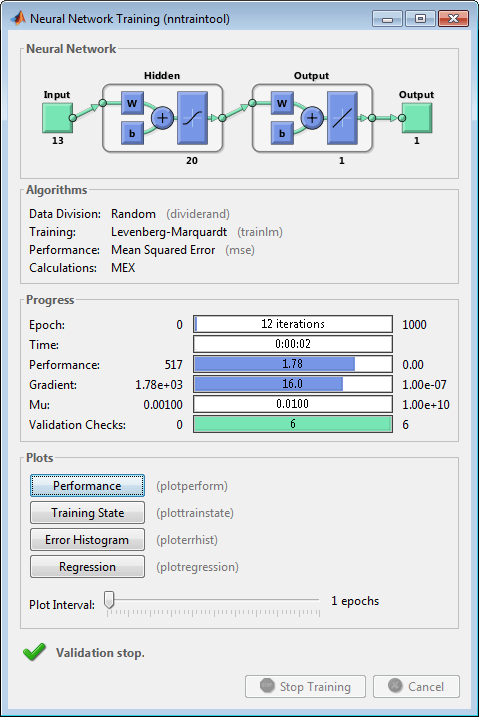
[net,tr] = train(net,bodyfatInputs,bodyfatTargets);Обратите внимание, что вам не нужно было выдавать configure , поскольку конфигурирование выполняется автоматически с помощью train функция. Во время обучения появится окно обучения, как показано на следующем рисунке. (Если вы не хотите, чтобы это окно отображалось во время обучения, вы можете установить параметр net.trainParam.showWindow кому false. Если требуется отобразить информацию об обучении в командной строке, можно задать параметр net.trainParam.showCommandLine кому true.)
В этом окне показано, что данные были разделены с помощью dividerand функция и Левенберг-Марквардт (trainlm) был использован метод обучения с функцией выполнения среднеквадратической ошибки. Напомним, что это настройки по умолчанию для feedforwardnet.
Во время обучения ход работ постоянно обновляется в окне обучения. Наибольший интерес представляют производительность, величина градиента производительности и количество проверок достоверности. Величина градиента и количество проверок достоверности используются для завершения обучения. Градиент станет очень маленьким, когда тренировка достигнет минимума производительности. Если величина градиента меньше 1e-5, тренировка прекратится. Этот предел можно скорректировать путем установки параметра net.trainParam.min_grad. Число проверок проверки представляет собой число последовательных итераций, в которых производительность проверки не может быть снижена. Если это число достигает 6 (значение по умолчанию), обучение прекращается. В этом прогоне можно увидеть, что обучение действительно остановилось из-за количества проверок проверки. Этот критерий можно изменить, задав параметр net.trainParam.max_fail. (Обратите внимание, что ваши результаты могут отличаться от тех, которые показаны на следующем рисунке, из-за случайной установки начальных весов и смещений.)
Существуют и другие критерии, которые можно использовать для прекращения обучения сети. Они перечислены в следующей таблице.
Параметр | Критерии остановки |
|---|---|
min_grad | Минимальная величина градиента |
max_fail | Максимальное число увеличений проверки |
time | Максимальное время обучения |
goal | Минимальное значение производительности |
epochs | Максимальное количество периодов обучения (итераций) |
Обучение также прекратится, если нажать кнопку Остановить обучение в окне обучения. Это может потребоваться, если функция производительности не может значительно снизиться во многих итерациях. Всегда можно продолжить обучение, переиздав train команда, показанная выше. Он продолжит обучение сети с момента завершения предыдущего прогона.
В окне обучения можно получить доступ к четырем графикам: производительность, состояние обучения, гистограмма ошибок и регрессия. График производительности показывает значение функции производительности по сравнению с номером итерации. В нем представлены результаты обучения, проверки и тестирования. График обучающего состояния показывает ход выполнения других обучающих переменных, таких как величина градиента, количество проверок достоверности и т.д. График гистограммы ошибок показывает распределение сетевых ошибок. График регрессии показывает регрессию между сетевыми выходами и сетевыми целями. Графики гистограммы и регрессии можно использовать для проверки производительности сети, как описано в разделе Анализ производительности неглубокой нейронной сети после обучения.
После обучения и проверки сети сетевой объект может использоваться для вычисления ответа сети на любой ввод. Например, если требуется найти сетевой ответ на пятый входной вектор в наборе данных здания, можно использовать следующее:
a = net(bodyfatInputs(:,5))
a = 27.3740
При выполнении этой команды выходные данные могут отличаться в зависимости от состояния генератора случайных чисел при инициализации сети. Ниже сетевой объект вызывается для вычисления выходов для параллельного набора всех входных векторов в наборе данных телесного жира. Это форма моделирования в пакетном режиме, в которой все входные векторы помещаются в одну матрицу. Это намного эффективнее, чем представление векторов по одному.
a = net(bodyfatInputs);
Каждый раз, когда нейронная сеть обучается, может привести к различному решению из-за различных начальных значений веса и смещения и различных разделов данных в обучающих, валидационных и тестовых наборах. В результате различные нейронные сети, обученные одной и той же проблеме, могут давать разные выходы для одного и того же входа. Чтобы была найдена нейронная сеть хорошей точности, переучивайтесь несколько раз.
Существует несколько других способов улучшения исходных решений, если требуется более высокая точность. Дополнительные сведения см. в разделе Улучшение неглубокого обобщения нейронных сетей и предотвращение переоборудования.