Документация

Время проектирования серии Время-задержка нейронных сетей

Начните с наиболее простой динамической сети, которая состоит из сети прямой связи с отводимой линией задержки на входе. Это называется сфокусированной нейронной сетью временной задержки (FTDNN). Это часть общего класса динамических сетей, называемых сфокусированными сетями, в которых динамика появляется только на входном уровне статической многослойной сети прямой связи. На следующем рисунке показана двухуровневая FTDNN.

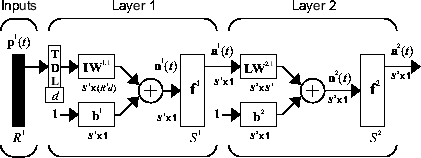
Эта сеть хорошо подходит для прогнозирования временных рядов. Следующий пример использования FTDNN для прогнозирования классического временного ряда.

Следующий рисунок представляет собой график нормализованных данных интенсивности, записанных с дальнего инфракрасного лазера в хаотическом состоянии. Это часть одного из нескольких наборов данных, используемых для конкурса временных рядов Santa Fe [WeGe94]. В конкурсе целью было использование первых 1000 очков временного ряда для прогнозирования следующих 100 очков. Поскольку наша цель состоит просто в том, чтобы проиллюстрировать, как использовать FTDNN для прогнозирования, сеть обучена здесь выполнять прогнозы на один шаг вперед. (Можно использовать результирующую сеть для многоступенчатых прогнозов, подавая прогнозы обратно на вход сети и продолжая итерацию.)

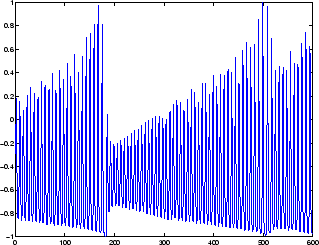
Первым шагом является загрузка данных, их нормализация и преобразование во временную последовательность (представленную массивом ячеек):

y = laser_dataset;
y = y(1:600);

Теперь создайте сеть FTDNN, используя timedelaynet команда. Эта команда аналогична команде feedforwardnet с дополнительным входом вектора линии задержки с отводом (первый вход). В этом примере используйте линию задержки с задержками от 1 до 8 и десять нейронов в скрытом слое:

ftdnn_net = timedelaynet([1:8],10);
ftdnn_net.trainParam.epochs = 1000;
ftdnn_net.divideFcn = '';

Организация сетевых входов и целей для обучения. Поскольку сеть имеет отводимую линию задержки с максимальной задержкой 8, начните с прогнозирования девятого значения временного ряда. Также необходимо загрузить линию задержки с отводом с восемью начальными значениями временного ряда (содержащимися в переменной Pi):

p = y(9:end);
t = y(9:end);
Pi=y(1:8);
ftdnn_net = train(ftdnn_net,p,t,Pi);

Обратите внимание, что вход в сеть совпадает с целевым. Поскольку в сети минимальная задержка составляет один шаг, это означает, что вы выполняете прогноз на один шаг вперед.

Во время обучения появляется следующее окно обучения.

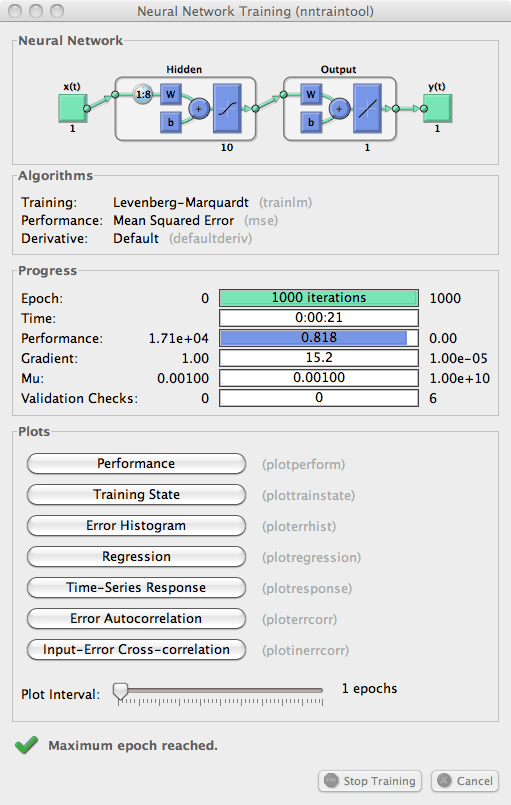
Тренировки прекратились, потому что была достигнута максимальная эпоха. В этом окне можно просмотреть отклик сети, нажав кнопку Time-Series Response. Появится следующий рисунок.

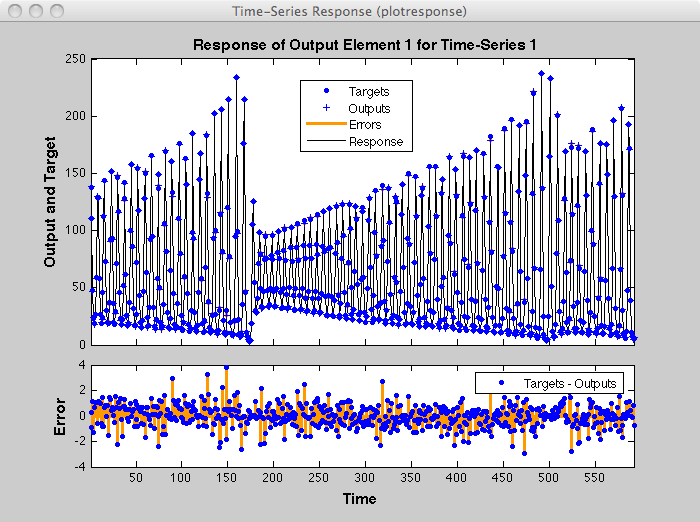
Теперь смоделируйте сеть и определите ошибку прогнозирования.

yp = ftdnn_net(p,Pi);
e = gsubtract(yp,t);
rmse = sqrt(mse(e))

rmse =
    0.9740

(Обратите внимание, что gsubtract - общая функция вычитания, которая может работать с массивами ячеек.) Этот результат намного лучше, чем вы могли бы получить, используя линейный предиктор. Это можно проверить с помощью следующих команд, которые создают линейный фильтр с тем же самым вводом линии задержки, что и предыдущий FTDNN.

lin_net = linearlayer([1:8]);
lin_net.trainFcn='trainlm';
[lin_net,tr] = train(lin_net,p,t,Pi);
lin_yp = lin_net(p,Pi);
lin_e = gsubtract(lin_yp,t);
lin_rmse = sqrt(mse(lin_e))

lin_rmse =
	21.1386

rms ошибка составляет 21.1386 для линейного предиктора, но 0,9740 для нелинейного предиктора FTDNN.

Отличительной особенностью FTDNN является то, что он не требует динамического обратного распространения для вычисления сетевого градиента. Это происходит потому, что линия задержки с отводом появляется только на входе сети и не содержит петель обратной связи или регулируемых параметров. По этой причине вы обнаружите, что эта сеть работает быстрее, чем другие динамические сети.

При наличии приложения для динамической сети сначала попробуйте использовать линейную сеть (linearlayer) и затем FTDNN (timedelaynet). Если ни одна из сетей не является удовлетворительной, попробуйте использовать одну из более сложных динамических сетей, рассмотренных в оставшейся части этой темы.

Каждый раз, когда нейронная сеть обучается, может привести к различному решению из-за различных начальных значений веса и смещения и различных разделов данных в обучающих, валидационных и тестовых наборах. В результате различные нейронные сети, обученные одной и той же проблеме, могут давать разные выходы для одного и того же входа. Чтобы была найдена нейронная сеть хорошей точности, переучивайтесь несколько раз.

Существует несколько других способов улучшения исходных решений, если требуется более высокая точность. Дополнительные сведения см. в разделе Улучшение неглубокого обобщения нейронных сетей и предотвращение переоборудования.

p = y(9:end);
t = y(9:end);
Pi = y(1:8);

[p,Pi,Ai,t] = preparets(ftdnn_net,y,y);

[X,Xi,Ai,T,EW,shift] = preparets(net,inputs,targets,feedback,EW)