Расчетный фильтр КИХ с ограниченной полосой частот
h = designFracDelayFIR(fd,TBW)fd и комбинированная полоса пропускания, по меньшей мере, TBW, где TBW < 0.999 и задается в нормированных частотных единицах. Функция автоматически определяет соответствующую длину N КИХ, для которой комбинированная полоса пропускания составляет по меньшей мере TBW.
Спроектируйте фильтр FIR с дробной задержкой, используя designFracDelayFIR функция. Передайте функцию в качестве входных аргументов задержку и длину фильтра. Варьируйте длину фильтра и наблюдайте влияние на измеренную объединенную полосу пропускания и номинальную групповую задержку.
Варьировать длину фильтра
Длина фильтра установлена равной 8
Укажите задержку 0,25 и длину фильтра 8 и создайте фильтр КИХ с дробной задержкой.
fd = 0.25; len = [8 32 64]; [h1,i10,bw1] = designFracDelayFIR(fd,len(1))
h1 = 1×8
-0.0086 0.0417 -0.1355 0.8793 0.2931 -0.0968 0.0341 -0.0074
i10 = 3
bw1 = 0.5810
Номинальная групповая задержка фильтра i10+fd равно 3,25 образца. Измеренная суммарная полоса пропускания фильтра составляет 0,5810 в нормированных частотных единицах.
Длина фильтра равна 32
Повторите процесс с длиной фильтра 32 отвода.
[h2,i20,bw2] = designFracDelayFIR(fd,len(2))
h2 = 1×32
-0.0001 0.0004 -0.0009 0.0017 -0.0029 0.0046 -0.0071 0.0104 -0.0148 0.0208 -0.0291 0.0410 -0.0594 0.0926 -0.1752 0.8983 0.2994 -0.1252 0.0758 -0.0515 0.0367 -0.0266 0.0193 -0.0139 0.0098 -0.0067 0.0044 -0.0028 0.0016 -0.0009 0.0004 -0.0001
i20 = 15
bw2 = 0.8571
Номинальная групповая задержка фильтра теперь равна 15,25 выборок. Увеличивая длину фильтра, целочисленная задержка i0 также увеличивается, что приводит к увеличению номинальной групповой задержки. Суммарная полоса пропускания фильтра увеличилась до 0,8571 в нормированных частотных единицах.
Длина фильтра установлена равной 64
Увеличьте длину фильтра до 64 отводов. Групповая задержка увеличивается до 31,25 отсчетов, а целочисленная задержка составляет 31 отсчет. Измеренная суммарная ширина полосы пропускания фильтра дополнительно увеличивается до 0,9219. Это покрытие полосы пропускания составляет 92,19% от общей полосы пропускания. Поскольку длина фильтра продолжает увеличиваться, комбинированная полоса пропускания стремится ближе к 1.
[h3,i30,bw3] = designFracDelayFIR(fd,len(3))
h3 = 1×64
-0.0000 0.0001 -0.0001 0.0002 -0.0003 0.0004 -0.0006 0.0008 -0.0010 0.0013 -0.0017 0.0022 -0.0027 0.0034 -0.0042 0.0051 -0.0061 0.0074 -0.0088 0.0105 -0.0125 0.0149 -0.0177 0.0212 -0.0255 0.0311 -0.0386 0.0494 -0.0664 0.0979 -0.1787 0.8997 0.2999 -0.1277 0.0801 -0.0575 0.0442 -0.0352 0.0288 -0.0239 0.0200 -0.0168 0.0142 -0.0120 0.0101 -0.0085 0.0071 -0.0059 0.0049 -0.0040
i30 = 31
bw3 = 0.9219
Характеристика величины графика
Постройте график результирующей амплитудной характеристики трех фильтров с помощью fvtool. Отметьте измеренную объединенную полосу пропускания трех фильтров. Увеличивая длину фильтра, можно увидеть, что измеренная суммарная полоса пропускания увеличивается.
hfv = fvtool(h1,1,h2,1,h3); ax = findall(hfv,"type","axes"); hline = findobj(ax(2),'Type','line'); xline(bw1, "LineStyle",'--', "LineWidth",2,'Color',hline(3).Color) xline(bw2, "LineStyle",'--', "LineWidth",2,'Color',hline(2).Color) xline(bw3, "LineStyle",'--', "LineWidth",2,'Color',hline(1).Color) title('Magnitude Responses in dB','FontSize',12) legend('Gain Response (N = 8)','Gain Response (N = 32)','Gain Response (N = 64)',... 'Measured Combined Bandwidth (N = 8)',... 'Measured Combined Bandwidth (N = 32)',... 'Measured Combined Bandwidth (N = 64)','Location','Southwest','FontSize',12);
Ответ на задержку группы графика
Постройте график ответа на групповую задержку трех фильтров с помощью fvtool. Отметьте номинальную групповую задержку i0 + fd трех фильтров. Увеличивая длину фильтра, можно увидеть, что номинальная групповая задержка увеличивается.
hfv = fvtool(h1,1,h2,1,h3,1,"Analysis","grpdelay"); ax = findall(hfv,"type","axes"); hline = findobj(ax(2),'Type','line'); yline(i10+fd, "LineStyle",'--', "LineWidth",2,'Color',hline(3).Color) yline(i20+fd, "LineStyle",'--', "LineWidth",2,'Color',hline(2).Color) yline(i30+fd, "LineStyle",'--', "LineWidth",2,'Color',hline(1).Color) title('Group Delay Responses','FontSize',12) legend('Group Delay Response (N = 8)','Group Delay Response (N = 32)','Group Delay Response (N = 64)',... 'Nominal Group Delay (N = 8)',... 'Nominal Group Delay (N = 32)',... 'Nominal Group Delay (N = 64)','Location','west','FontSize',12); ax(1).YLim = [-10,40];
Спроектируйте фильтр FIR с дробной задержкой, используя designFracDelayFIR функция. Передайте функцию в качестве входных аргументов задержку и объединенную полосу пропускания.
Укажите задержку 0,786, а целевую объединенную полосу пропускания 0,8. Функция создает фильтр, который имеет длину 22 отвода, целочисленную задержку i0, равную 10 выборкам, и комбинированную полосу пропускания. mbw 0,8044 в нормированных частотных единицах. Это значение mbw делает покрытие комбинированной полосы пропускания 80,44% частотной области и превышает заданную целевую комбинированную полосу пропускания. Номинальная групповая задержка фильтра i0+fd равно 10,786.
fd = 0.786; tbw = 0.8; [h,i0,mbw] = designFracDelayFIR(fd, tbw)
h = 1×22
0.0003 -0.0011 0.0026 -0.0052 0.0094 -0.0156 0.0248 -0.0386 0.0611 -0.1052 0.2512 0.9225 -0.1548 0.0769 -0.0455 0.0281 -0.0173 0.0102 -0.0057 0.0028 -0.0012 0.0003
i0 = 10
mbw = 0.8044
Постройте график импульсной характеристики FIR.
stem((0:length(h)-1),h); xlabel('h'); ylabel('h[n]'); title('Impulse Response of the Fractional Delay FIR')
Постройте график результирующей амплитудной характеристики и групповой задержки с использованием fvtool. Отметьте номинальную групповую задержку и объединенную полосу пропускания фильтра.
hfv = fvtool(h,'Analysis','magnitude','OverlayedAnalysis','grpdelay'); ax = findall(hfv,'type','axes'); xline(mbw, 'LineStyle',':', 'Color','b', 'LineWidth',2) xline(tbw, 'LineStyle','--', 'Color','m', 'LineWidth',2) yline(ax(1),i0+fd, 'LineStyle',':','Color','r','LineWidth',1) yticks(ax(1),[i0, i0+fd,i0+1:i0+9]); yticklabels(ax(1),'auto') legend('Gain Response','Measured Combined Bandwidth',... 'Target Combined Bandwidth','Group Delay Response','Nominal Group Delay', ... 'Location','west','FontSize',12) grid off
Спроектируйте фильтр FIR с дробной задержкой, используя designFracDelayFIR функция. Определите групповую задержку проектируемого фильтра. Создать dsp.FIRFilter объект, который использует эти расчетные коэффициенты и, следовательно, имеет одинаковую групповую задержку. В качестве альтернативы создайте выборочную последовательность известной функции. Передайте отобранную последовательность в фильтр FIR. Сравните выходные данные КИХ-фильтра со сдвинутыми выборками известной функции. Задайте, чтобы этот сдвиг был равен групповой задержке фильтра FIR. Убедитесь, что две последовательности совпадают.
Укажите, что задержка фильтра КИХ с дробной задержкой должна составлять 1/3, а длина - 6 отводов.
fd = 1/3; len = 6;
Спроектируйте фильтр с помощью designFracDelayFIR функция и определение индекса центра i0 и комбинированной полосы пропускания bw фильтра. Групповая задержка разработанного фильтра: i0 + fd или приблизительно 2,33 для полосы пропускания bw.
[h,i0,bw] = designFracDelayFIR(fd,len)
h = 1×6
0.0293 -0.1360 0.7932 0.3966 -0.1088 0.0257
i0 = 2
bw = 0.5158
Создать dsp.FIRFilter и установить его числитель на коэффициенты h фильтра. Этот фильтр теперь фактически является КИХ-фильтром с дробной задержкой. Убедитесь, что ответ на групповую задержку этого фильтра составляет приблизительно 2,33 для длительности полосы пропускания bw.
fdf = dsp.FIRFilter(h); grpdelay(fdf)
Сравнение со смещенной функцией
Определите последовательность x как образцы известной функции.
f = @(t) (0.1*t.^2+cos(0.9*t)).*exp(-0.1*(t-5).^2);
n = (0:19)'; t = linspace(0,19,512);
x = f(n); % SamplesПостройте график выбранных значений x относительно исходной известной функции f (t).
scatter(n,x,20,'k','filled'); hold on; plot(t,f(t),'color',[0.5 0.5 0.5],'LineWidth',0.5) hold off; xlabel('Time') legend(["Input Samples","f(t)"]) title('Input Sequence with Known Underlying Analog Signal') ax = gca; ax.XGrid='on';
Пропустите отобранную последовательность x через фильтр FIR. Постройте график последовательности ввода и последовательности вывода.
y = fdf(x); subplot(2,1,1); stem(x); title('Input Sequence'); xlabel('n') subplot(2,1,2) stem(y); title('FIR Output Sequence'); xlabel('n')
Сдвигать последовательность ввода по горизонтали на i0 + fd, что равно групповой задержке фильтра FIR. Постройте график функции f (t-i0-FD). Убедитесь, что входные и выходные последовательности примерно соответствуют сдвинутой функции.
figure scatter(n,y,20,'red','filled') hold on; scatter(n+i0+fd,x,20,'black','filled') plot(t,f(t-i0-fd),'Color',[1,0.5,0.5],'LineWidth',0.1) xlabel('Time') legend(["Filter output","Shifted Input Samples","Shifted f(t-i0-fd)"]) hold off grid on title('Input and Output Sequences Aligned and Overlaid')
h - Коэффициенты фильтра КИХ дробной задержкиКоэффициенты КИХ-фильтра дробной задержки, возвращаемые в виде вещественного значения N-длинный вектор строки. Когда дробная задержка является единственным входом в функцию, функция создает фильтр длиной 50. Ширина полосы пропускания для этого фильтра по умолчанию составляет приблизительно 0,9. Если указан второй входной аргумент, функция создает фильтр в соответствии со следующим:
Если для второго входного аргумента функции задано значение больше 1, функция обрабатывает это значение как требуемую длину фильтра и возвращает фильтр, который является N отводы длинные.
Если для второго входного аргумента функции задано значение меньше 0.999, функция обрабатывает это значение как требуемую комбинированную полосу пропускания TBWопределяет соответствующую длину фильтра и проектирует фильтр соответствующим образом.
Типы данных: single | double
i0 - Целочисленная задержкаЦелочисленная задержка разработанного фильтра FIR, возвращаемая как целочисленное значение. Целочисленная задержка является наименьшим целочисленным сдвигом, необходимым для причинно-следственной связи симметричного окна Кайзера. Это значение приблизительно равно половине длины фильтра, N/2. Дополнительные сведения см. в разделе Целочисленная задержка, i0.
Номинальная групповая задержка фильтра задается i0+fd.
Типы данных: single | double
MBW - Измеренная комбинированная полоса пропускания0.999Измеренная комбинированная полоса пропускания, возвращаемая как действительный положительный скаляр, который меньше 0.999. Это значение комбинированной полосы пропускания проектируемого фильтра. Комбинированная полоса пропускания определяется как минимум полосы пропускания усиления и полосы пропускания групповой задержки.
При указании второго входного аргумента значение меньше 0.999, функция обрабатывает это значение как целевую комбинированную полосу пропускания TBW. Функция проектирует фильтр таким образом, чтобы измеренная комбинированная полоса пропускания MBW соответствует или превышает целевую комбинированную полосу пропускания TBW. Длина фильтра определяется таким образом, что это ограничение полосы пропускания выполняется.
При указании второго входного аргумента и целочисленном значении, большем 1, функция обрабатывает это значение как требуемую длину N фильтра. Измеренная комбинированная полоса пропускания в этом случае зависит от заданной длины. Больше значение N, выше измеренная комбинированная полоса пропускания MBW. См. график ниже, на котором показан этот вариант. По мере увеличения длины фильтра комбинированная полоса пропускания фильтра перемещается ближе к 1. Красная пунктирная вертикальная линия обозначает объединенную полосу пропускания для каждой длины. Значение дробной задержки для каждого из этих фильтров установлено равным 0,3.
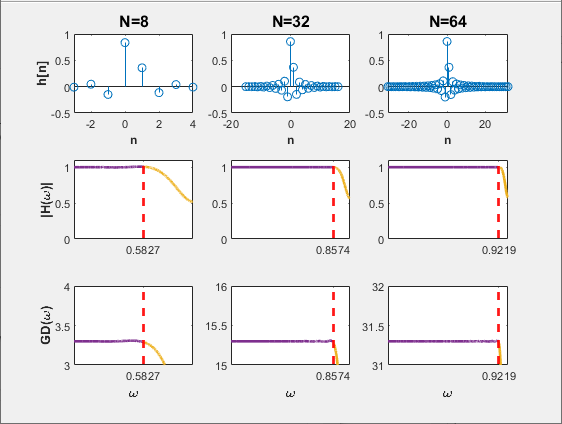
Типы данных: single | double
КИХ-фильтр дробной задержки - это аппроксимация КИХ идеального синк-фильтра сдвига с заданным значением дробной (не целочисленной) задержки. fd в пределах [0,1].
Идеальный фильтр сдвига моделирует D/A-интерполятор с ограниченной полосой частот с последующей сдвинутой A/D равномерной выборкой. Предполагая равномерную частоту дискретизации и инвариантную интерполяцию сдвига, результирующая общая система может быть выражена как фильтр свертки, аппроксимированный фильтром КИХ. Другими словами, , который инкапсулирует цепочку D/A-интерполяции, сдвига и A/D-дискретизации, как показано на чертеже.
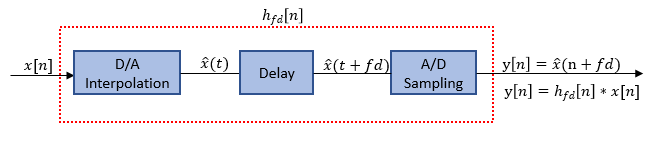
где,
=∑kx[k]sinc (t + fd − k)
Частотная характеристика идеального фильтра сдвига задается следующим уравнением:
jü fd
Идеальный фильтр сдвига имеет плоскую единичную характеристику усиления и постоянную групповую задержку, равную fd, где fd - указанное значение дробной задержки.
Аппроксимация КИХ получается путем усечения идеального фильтра и взвешивания усеченного фильтра окном Кайзера.
+ fd)· KN, β [m]
где, m] - кайзеровское окно длинойN и имеет параметр формы β. Окно Кайзера предназначено для оптимизации частотной характеристики КИХ, максимизируя объединенные полосы частот как характеристики усиления, так и характеристики групповой задержки.
Чтобы сделать приближение FIR причинным, дополнительный сдвиг i0 вводят номинальную групповую задержку фильтра, равную i0+fd. Частотная характеристика усеченного фильтра задается как, fd + i0).
Дополнительные сведения см. в разделе Целочисленная задержка, i0.
i0Целочисленная задержка, i0, является наименьшим целым сдвигом, который требуется, чтобы сделать симметричное окно Кайзера причинным.
Идеал sinc фильтр сдвига является фильтром allpass, который имеет бесконечную и некаузальную импульсную характеристику. Для аппроксимации этого фильтра функция использует конечное индексное окно Кайзера длины N который симметричен вокруг начала координат и захватывает основную долю sinc функция.
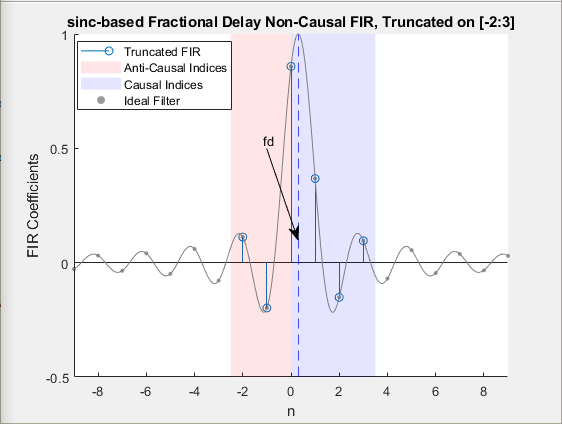
Из-за симметричного характера окна половина окна (приблизительно равная N/2) находится на отрицательной стороне начала координат, делая усеченный фильтр антикаузальным. Чтобы сделать усеченный фильтр причинно-следственным, сдвиньте антикаузальную (отрицательные индексы) часть окна FIR на целую задержку, i0, что приблизительно равно N/2.
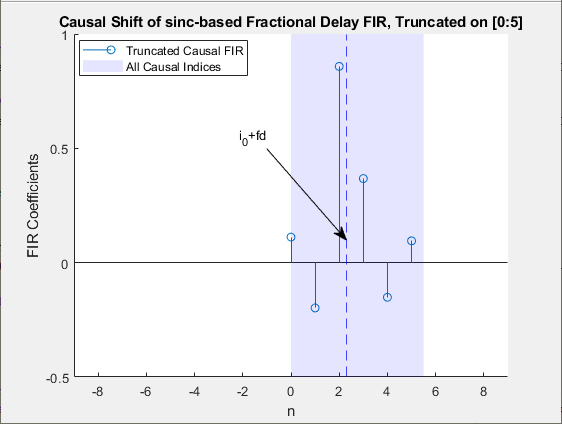
Общая задержка каузального фильтра FIR составляет i0+fd, где fd - указанное значение дробной задержки.
Дополнительные сведения о приближении КИХ см. в разделе «Приблизительные значения КИХ в причинно-следственной связи» в разделе «Идеальный фильтр сдвига sinc» в разделе «Проектирование фильтров КИХ с дробной задержкой».