В системе слежения за множеством целей (МТТ) один или более датчиков генерируют множество обнаружений от множества целей при сканировании. Для отслеживания этих целей один важный шаг состоит в том, чтобы правильно назначить эти обнаружения целям или дорожкам, поддерживаемым в трекере, чтобы эти обнаружения могли использоваться для обновления этих дорожек. Если количество целей или обнаружений велико или существуют конфликты между различными гипотезами назначения, назначение обнаружений является сложной задачей.
В зависимости от измерения присвоения проблемы присвоения можно разделить на следующие категории:
Задача назначения 2-D - присваивает n целей m наблюдениям. Например, назначьте 5 дорожек 6 обнаружениям, сгенерированным одним датчиком за один шаг.
Задача назначения S-D - присваивает n целей набору (m1, m2, m3,...) наблюдений. Например, назначьте 5 дорожек 6 обнаружениям от одного датчика и 4 обнаружениям от другого датчика одновременно. Этот пример является типичной проблемой назначения 3-D.
Чтобы проиллюстрировать основную идею проблемы назначения, рассмотрим простой пример назначения 2-D. Одна компания пытается назначить 3 рабочих места 3 работникам. Из-за различных уровней опыта работников не все работники могут выполнять каждую работу с одинаковой эффективностью. Стоимость (в часах) каждого работника для завершения каждого задания определяется матрицей затрат, показанной в таблице. Правило назначения состоит в том, что каждый работник может взять только одно задание, а одно задание может взять только один работник. Чтобы гарантировать эффективность, целью этого задания является минимизация общих затрат.
Рабочий | Работа | ||
| 1 | 2 | 3 | |
| 1 | 41 | 72 | 39 |
| 2 | 22 | 29 | 49 |
| 3 | 27 | 39 | 60 |
Поскольку количество работников и рабочих мест в этом примере невелико, все возможные назначения могут быть получены путем перечисления, а решение по минимальным затратам выделено в таблице парами назначений (1, 3), (2, 2) и (3, 1). На практике, когда размер назначения становится больше, оптимальное решение трудно получить для 2-D назначения. Для задачи назначения S-D оптимальное решение может быть недоступно на практике.
В 2-D проблеме назначения MTT трекер пытается назначить несколько дорожек нескольким обнаружениям. Помимо проблемы размерности, упомянутой выше, несколько других факторов могут существенно изменить сложность назначения:
Распределение цели или обнаружения - если цели распределены редко, связать цель с ее соответствующим обнаружением относительно просто. Однако, если целевые объекты или обнаруженные объекты распределены плотно, назначения становятся неоднозначными, потому что назначение целевого объекта обнаружению или другому близлежащему обнаружению редко вносит какие-либо различия в стоимость.
Вероятность обнаружения (Pd) датчика - Pd описывает вероятность обнаружения цели датчиком, если цель находится в поле зрения датчика. Если Pd датчика мал, то истинная цель может не вызвать никакого обнаружения во время сканирования датчика. В результате дорожка, представленная истинной целью, может украсть обнаружения с других дорожек.
Разрешение датчика - разрешение датчика определяет способность датчика отличать обнаруженные объекты от двух целей. Если разрешение датчика низкое, то две близлежащие цели могут привести только к одному обнаружению. Это нарушает распространенное предположение, что каждое обнаружение может быть назначено только одной дорожке и приводит к неразрешимым конфликтам назначения между дорожками.
Загромождение или частота ложных аварийных сигналов датчика - ложные аварийные сигналы вводят дополнительные возможные назначения и, следовательно, увеличивают сложность назначения данных.
Сложность задачи назначения может определить, какие методы назначения применять. В инструментарии Sensor Fusion and Tracking Toolbox™ используются три подхода назначения 2-D, соответствующих трем различным трекерам:
trackerGNN - использует глобальный подход назначения ближайших данных
trackerJPDA - использует совместный подход ассоциации вероятностных данных
trackerTOMHT - использует подход отслеживания множественных гипотез, ориентированный на трекер
Следует отметить, что каждый трекер обрабатывает данные от датчиков последовательно, что означает, что каждый трекер имеет дело только с проблемой назначения с обнаружениями одного датчика за раз. Даже при таком лечении может быть слишком много пар назначения. Для уменьшения количества пар дорожек и обнаружения, рассматриваемых для назначения, часто используется метод стробирования.
Стробирование является механизмом скрининга для определения того, какие наблюдения являются действительными кандидатами для обновления существующих дорожек и исключения маловероятных пар обнаружение-дорожка, используя информацию о распределении прогнозируемых дорожек. Чтобы установить проверочный затвор для дорожки при текущем сканировании, расчетная дорожка для текущего шага прогнозируется из предыдущего шага.
Например, трекер подтверждает дорожку в момент времени tk и принимает несколько обнаружений в момент времени tk + 1. Чтобы сформировать вентиль проверки в момент времени tk + 1, трекеру сначала необходимо получить предсказанное измерение как:
^ k + 1 | k)
где![]() - оценка дорожки, предсказанная с момента времени tk, и
- оценка дорожки, предсказанная с момента времени tk, и![]() - модель измерения, которая выводит ожидаемое измерение с учетом состояния дорожки. Остаточный вектор наблюдения равен
- модель измерения, которая выводит ожидаемое измерение с учетом состояния дорожки. Остаточный вектор наблюдения равен
где yk + 1 - фактическое измерение. Чтобы установить границу затвора, остаточная ковариация S обнаружения используется для формирования эллипсоидального вентиля проверки достоверности. Эллипсоидальный затвор, который устанавливает пространственную эллипсоидальную область в пространстве измерения, определяется на расстоянии Махаланобиса как:
=y˜TS−1y˜≤G
где G - пороговое значение стробирования, которое можно указать на основе требования назначения. Увеличение порога может включать больше обнаружений в затвор.
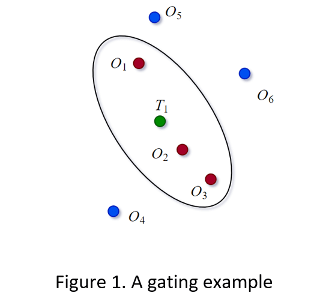
После того как затвор назначения установлен для каждой дорожки, состояние стробирования каждого обнаружения yi (i = 1,..., n) может быть определено путем сравнения его расстояния Махаланобиса d2 (yi) с порогом стробирования G. Если d2 (yi) < G, то обнаружение yi находится внутри затвора дорожки и будет рассматриваться для ассоциации. В противном случае возможность обнаружения, связанного с дорожкой, удаляется. На фиг.1 T1 представляет прогнозируемую оценку дорожки, и O1- O6 представляют собой шесть обнаружений. На основе результата стробирования O1, O2 и O3 находятся в пределах литника проверки на рисунке.
Метод GNN является методом назначения единой гипотезы. Для каждого нового набора данных целью является назначение глобальных ближайших наблюдений существующим дорожкам и создание новых гипотез дорожек для неназначенных обнаружений.
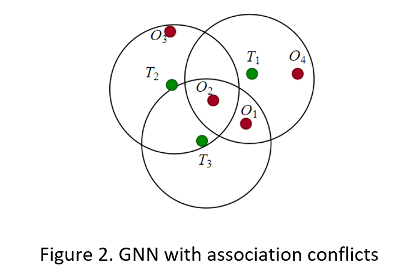
Проблема назначения GNN может быть легко решена, если нет конфликтов ассоциаций между дорожками. Трекеру необходимо только назначить дорожку ближайшему соседу. Тем не менее, конфликтные ситуации (см. фиг.2) возникают, когда имеется более одного наблюдения в вентиле проверки подлинности дорожки или наблюдение находится в вентилях более чем одной дорожки. Для разрешения этих конфликтов трекер должен оценить матрицу затрат.
Элементы матрицы затрат для метода GNN включают расстояние от дорожек до обнаружений и другие факторы, которые можно рассмотреть. Например, один подход заключается в определении обобщенного статистического расстояния между наблюдением j для отслеживания i как:
Sij |)
где dij - расстояние Махаланобиса и ln (| Sij |), логарифм определителя матрицы остаточной ковариации, используется для наказания дорожек с большей неопределенностью предсказания.
Для задачи назначения, приведенной на фиг.2, следующая таблица показывает гипотетическую матрицу затрат. Неразрешенные назначения, которые не прошли проверку стробирования, обозначаются X. (На практике затраты на неразрешенные назначения могут обозначаться большими значениями, такими как 1000.)
Следы | Наблюдения | |||
| O1 | O2 | O3 | O4 | |
| T1 | 9 | 6 | X | 6 |
| T2 | X | 3 | 10 | X |
| T2 | 8 | 4 | X | X |
Для этой проблемы выделенное оптимальное решение можно найти путем перечисления. O3 обнаружения не назначен, поэтому трекер будет использовать его для создания новой предварительной дорожки. Для более сложных задач назначения GNN требуются более точные формулировки и более эффективные алгоритмы для получения оптимального или неоптимального решения.
Общая проблема назначения 2-D может быть сформирована следующим образом. Учитывая элемент матрицы затрат Cij, найдите назначение Z = {zij}, которое минимизирует
с учетом двух ограничений:
Если дорожка i назначена наблюдению j, то zij = 1. В противном случае zij = 0. zi0 = 1 представляет гипотезу о том, что дорожка i не назначена никакому обнаружению. Аналогично, z0j = 1 представляет гипотезу, что наблюдение j не назначено ни одной дорожке. Первое ограничение означает, что каждое обнаружение может быть назначено не более чем одной дорожке. Второе ограничение означает, что каждая дорожка может быть назначена не более чем одному обнаружению.
Sensor Fusion and Tracking Toolbox предоставляет множество функций для решения 2-D проблем назначения GNN:
assignmunkres - использует алгоритм Манкра, который гарантирует оптимальное решение, но может потребовать больше операций вычисления.
assignauction - использует алгоритм аукциона, который требует меньшего количества операций, но может сходиться в оптимальном или неоптимальном решении.
assignjv - использует алгоритм Joker-Volgenant, который также сходится на оптимальном или неоптимальном решении, но обычно с более высокой скоростью схождения.
В trackerGNN, можно выбрать алгоритм назначения, указав Assignment собственность.
Из-за неопределенности характера проблем назначения, только получение решения (оптимального или неоптимального) может быть недостаточным. Чтобы учесть несколько гипотез о назначении между дорожками и обнаружениями, требуется несколько неоптимальных решений. Эти неоптимальные решения называются К лучшими решениями задачи назначения.
К лучших решений обычно получают варьированием решения, полученного любой из ранее упомянутых функций назначения. Затем на следующем этапе алгоритм K наилучшего решения удаляет одну пару дорожек к обнаружению в исходном решении и находит следующее наилучшее решение. Например, для этой матрицы затрат:
каждая строка представляет стоимость, связанную с дорожкой, а каждый столбец представляет стоимость, связанную с обнаружением. Как было подчеркнуто, оптимальным решением является (7,15,16, 9) со стоимостью 47. На следующем шаге удалите первую пару (соответствующую 7), и следующим лучшим решением будет (10,15, 20, 22) со стоимостью 67. После этого удалите вторую пару (соответствующую 15), и следующим лучшим решением будет (7, 5,16, 9) со стоимостью 51. После нескольких шагов пять лучших решений:
| Решение | Стоимость |
| (7,15,16, 9) | 47 |
| (7,5,17, 22) | 51 |
| (7,15, 8, 22) | 52 |
| (7, 21,16, 9) | 53 |
| (7, 21,17, 9) | 53 |
См. пример поиска пяти лучших решений с помощью Assignkbest, в котором используется assignkbest функция, чтобы найти К лучших решений.
В то время как метод GNN делает жесткое назначение обнаружения дорожке, метод JPDA применяет мягкое назначение, так что все обнаружения в пределах вентиля проверки достоверности дорожки могут вносить взвешенный вклад в дорожку на основе их вероятности ассоциации.
Например, для результатов стробирования, показанных на фиг.1, трекер JPDA вычисляет возможность ассоциации между T1 дорожек и наблюдениями O1, O2 и O3. Предположим, что вероятность ассоциации этих трех наблюдений равна p11, p12 и p13, и их остатки относительно T1 дорожки равны, ![]()
![]() и,
и, ![]() соответственно. Тогда взвешенная сумма остатков, связанных с дорожкой T1, равна:
соответственно. Тогда взвешенная сумма остатков, связанных с дорожкой T1, равна:
В трекере взвешенный остаток используется для обновления T1 дорожки на этапе коррекции фильтра трекинга. В фильтре вероятность отмены назначения, p10, также требуется для обновления дорожки T1. Дополнительные сведения см. в разделе Алгоритм коррекции JPDA для дискретного расширенного фильтра Калмана.
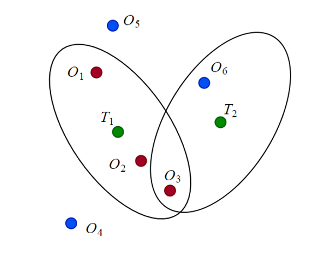
Метод JPDA требует еще одного шага при наличии конфликтов между назначениями в разных треках. Например, на следующем рисунке отслеживаются конфликты T2 с T1 о назначении O3 наблюдения. Поэтому для вычисления вероятности p13 ассоциации должна быть учтена совместная вероятность того, что T2 не назначен O3 (то есть T2 назначен O6 или не назначен).
В отличие от метода JPDA, который объединяет все обнаружения в пределах вентиля проверки с использованием взвешенной суммы, метод TOMHT генерирует множество гипотез или ветвей дорожек на основе обнаружений в вентиле и распространяет ветви высокого правдоподобия между шагами сканирования. После распространения эти гипотезы могут быть проверены и отсечены на основе нового набора обнаружений.
Например, для сценария стробирования, показанного на фиг.1, TOMHT-трекер рассматривает следующие четыре гипотезы:
Не назначать обнаружение T1, приводящим к гипотезе T10
Присвойте O1 T1, что приводит к гипотезе T11
Присвойте O2 T1, что приводит к гипотезе T12
Присвойте O3 T1, что приводит к гипотезе T13
Учитывая порог назначения, трекер вычисляет возможность каждой гипотезы и отбрасывает гипотезы с вероятностью ниже порога. Гипотетически, если только p10 и p11 больше порога, то только T10 и T11 распространяются на следующий этап для обновления обнаружения.
В задаче назначения S-D размерность назначения S больше 2. Обратите внимание, что все три трекера (trackerGNN, trackerJPDA, и trackerTOMHT) обнаружения процессов от каждого датчика последовательно, что приводит к проблеме назначения 2-D. Однако для некоторых приложений требуется трекер, который обрабатывает одновременные наблюдения с нескольких датчиков одновременно, что требует решения проблемы назначения S-D. Между тем, назначение S-D широко используется в отслеживающих приложениях, таких как слияние статических данных, которое предварительно обрабатывает данные обнаружения перед подачей в трекер.
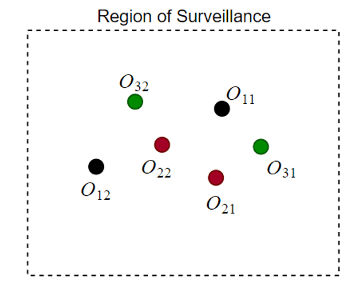
Проблема назначения S-D для слияния статических данных включает S-сканирование области наблюдения с нескольких датчиков одновременно, и каждое сканирование состоит из нескольких обнаружений. Источниками обнаружения могут быть реальные цели или ложные сигналы тревоги. Объект заключается в обнаружении неизвестного количества целей и оценке их состояний. Например, как показано на фиг.4, три сканирования датчиков производят шесть обнаружений. Обнаруженные объекты одного цвета относятся к одному и тому же сканированию. Поскольку каждое сканирование генерирует два обнаружения, в области наблюдения, вероятно, имеются две цели. Чтобы выбрать различные возможности присвоения или ассоциации, проанализируйте матрицу затрат.
Расчет стоимости может зависеть от многих факторов, таких как расстояние между обнаружениями и ковариационное распределение каждого обнаружения. Для иллюстрации базовой концепции затраты на распределение по нескольким гипотезам гипотетически приведены в таблице [1].
| Гипотезы назначения | Первые наблюдения сканирования (O1x) | Второе наблюдение сканирования (O2x) | Третье наблюдение сканирования (O3x) | Стоимость |
| 1 | 0 | 1 | 1 | −10.2 |
| 2 | 1 | 2 | 0 | −10.9 |
| 3 | 1 | 1 | 1 | −18.0 |
| 4 | 1 | 1 | 2 | −14.8 |
| 5 | 1 | 2 | 1 | −17.0 |
| 6 | 2 | 0 | 1 | −13.2 |
| 7 | 2 | 0 | 2 | −10.6 |
| 8 | 2 | 2 | 0 | −11.1 |
| 9 | 2 | 1 | 2 | −14.1 |
| 10 | 2 | 2 | 2 | −16.7 |
В таблице 0 обозначает, что дорожка связана с отсутствием обнаружения в этом сканировании. Предположим, что гипотезы, не показанные в таблице, усекаются стробированием или игнорируются из-за высоких затрат. Для краткого представления каждой дорожки используйте cijk для представления стоимости связи наблюдения i в сканировании 1, j в сканировании 2 и k в сканировании 3. Например, для гипотезы назначения 1 c011 = -10.2. Несколько гипотез трека конфликтуют с другими в таблице. Например, два наиболее вероятных назначения, c111 и c121 несовместимы, поскольку они имеют одно и то же наблюдение в сканированиях 1 и 3.
Целью решения задачи назначения S-D является поиск наиболее вероятной совместимой гипотезы назначения, учитывающей все обнаружения. Однако, когда S ≥ 3, проблема, как известно, масштабируется с количеством дорожек и обнаружений с экспоненциальной скоростью (NP-жесткий). Метод релаксации Лагранжа обычно используется для получения оптимального или субоптимального решения для задачи назначения S-D эффективно.
Три сканирования данных имеют ряд M1, M2 и M3 наблюдений, соответственно. Обозначим наблюдение сканирования 1, 2 и 3 как i, j и k соответственно. Например, i = 1, 2,..., M1. Используйте zijk, чтобы представить гипотезу формирования дорожки для O1i, O2j и O3k. Если гипотеза верна, то zijk = 1; в противном случае zijk = 0. Как уже упоминалось, cijk используется для представления стоимости ассоциации zijk. cijk равен 0 для ложных тревог и отрицателен для возможных ассоциаций. Задача оптимизации S-D может быть сформулирована следующим образом:
=mini,j,k∑i=0M1∑j=0M2∑k=0M3cijkzijk
с учетом трех ограничений:
M2∑j=0M2∑k=0M3zijk=1,∀i=1,2,..., M1
Функция оптимизации выбирает связи для минимизации общей стоимости. Три ограничения обеспечивают учет каждого обнаружения (либо включенного в назначение, либо обработанного как ложный аварийный сигнал).
Метод релаксации Лагранжа подходит к этой проблеме назначения 3-D путем ослабления первого ограничения с использованием множителей Лагранжа. Определите новую функцию L (λ):
=∑k=0M3λk[∑i=0M1∑j=0M2zijk−1]
где λ k, k = 1, 2,..., M3 - множители Лагранжа. Вычтите L из исходной объектной функции J (z), чтобы получить новую объектную функцию, и первое ограничение в k ослабляется. Поэтому проблема назначения 3-D сводится к проблеме назначения 2-D, которая может быть решена любым из способов назначения 2-D. Для получения дополнительной информации см. [1 ].
Метод лагранжевой релаксации позволяет мягко нарушить первое ограничение, и поэтому может гарантировать только неоптимальное решение. Однако для большинства приложений этого достаточно. Чтобы указать точность решения, метод использует зазор решения, который определяет разницу между текущим решением и потенциально оптимистичным решением. Зазор неотрицателен, и меньший зазор раствора соответствует решению, более близкому к оптимальному решению.
Панель инструментов для слияния и отслеживания датчиков assignsd для решения для S-D назначения с использованием метода лагранжевой релаксации. Аналогично решателю назначения K best 2-D assignkbest, панель инструментов также предоставляет K лучший решатель назначения S-D, assignkbestsd, который используется для предоставления нескольких неоптимальных решений для задачи назначения S-D.
См. раздел Отслеживание использования распределенных синхронных пассивных датчиков для применения назначения S-D в синтезе статического обнаружения.
assignauction | assignjv | assignkbest | assignkbestsd | assignmunkres | assignsd | assignTOMHT | trackerGNN | trackerJPDA | trackerTOMHT
[1] Блэкман, С. и Р. Пополи. Проектирование и анализ современных систем слежения. Радарная библиотека Artech House, Бостон, 1999 год.
[2] Мусицки, Д. и Р. Эванс. «Совместная ассоциация комплексных вероятностных данных: JIPDA». Сделки IEEE по аэрокосмическим и электронным системам. Том 40, номер 3, 2004, стр. 1093 -1099.