В последние годы количество и разнообразие применений нечеткой логики значительно возросло. Диапазон применений варьируется от потребительских продуктов, таких как камеры, видеокамеры, стиральные машины и микроволновые печи, до управления промышленными процессами, медицинского оборудования, систем поддержки принятия решений и выбора портфеля.
Чтобы понять, почему выросло использование нечеткой логики, необходимо сначала понять, что подразумевается под нечеткой логикой.
Нечеткая логика имеет два разных значения. В узком смысле нечеткая логика - это логическая система, которая является расширением многозначной логики. Однако в более широком смысле нечёткая логика (FL) почти синонимична теории нечётких множеств, теории, относящейся к классам объектов без чётких, чётко определённых границ. В таких случаях членство в наборе является вопросом степени. В этой перспективе нечеткая логика в её узком смысле является ветвью FL. Даже по своему более узкому определению нечеткая логика отличается как по концепции, так и по существу от традиционных многозначных логических систем.
В программном обеспечении Fuzzy Logic Toolbox™ нечеткая логика должна интерпретироваться как FL, то есть нечеткая логика в её широком смысле. Основные идеи, лежащие в основе FL, объясняются в «Основах нечеткой логики». Можно добавить, что основной концепцией, лежащей в основе ФЛ, является концепция лингвистической переменной, то есть переменной, значения которой являются словами, а не числами. В действительности, большая часть ФЛ может рассматриваться как методология для вычисления словами, а не числами. Хотя слова по своей сути менее точны, чем цифры, их использование ближе к человеческой интуиции. Кроме того, вычисления словами используют допуск неточности и тем самым снижают стоимость решения.
Другой основной концепцией в FL, которая играет центральную роль в большинстве его приложений, является нечеткое правило if-then или, просто, нечеткое правило. Хотя основанные на правилах системы имеют долгую историю использования в искусственном интеллекте (ИИ), в таких системах отсутствует механизм для борьбы с нечеткими последующими и нечеткими предшествующими. В нечеткой логике этот механизм обеспечивается исчислением нечетких правил. Расчет нечетких правил служит основой для того, что можно назвать нечетким языком зависимостей и команд (FDCL). Хотя FDCL явно не используется в инструментарии, он фактически является одним из его основных компонентов. В большинстве применений нечеткой логики нечеткое логическое решение в действительности является трансляцией человеческого решения в FDCL.
Тенденция, которая растет в видимости, связана с использованием нечеткой логики в сочетании с нейрокомпьютерными и генетическими алгоритмами. В более общем смысле, нечеткая логика, нейрокомпьютеры и генетические алгоритмы могут рассматриваться как основные составляющие того, что можно назвать мягкими вычислениями. В отличие от традиционных, жестких вычислений, мягкие вычисления вмещают неточность реального мира. Основной принцип мягких вычислений: использовать допуск неточности, неопределенности и частичной правды для достижения прослеживаемости, надежности и низкой стоимости решения. В будущем мягкие вычисления могут играть все более важную роль в разработке и разработке систем, MIQ (Machine IQ) которых намного выше, чем системы, разработанные обычными способами.
Среди различных комбинаций методологий в мягких вычислениях та, которая имеет самую высокую видимость на данном этапе, является нечеткой логикой и нейрокомпьютером, что приводит к нейро-нечетким системам. В рамках нечеткой логики такие системы играют особенно важную роль в индукции правил из наблюдений. Эффективный метод, разработанный доктором Роджером Чаном для этой цели, называется ANFIS (Adaptive Neuro-Fuzzy Inverence System). Этот метод является важным компонентом панели инструментов.
Нечеткая логика аппроксимирует человеческие рассуждения и хорошо помогает сбалансировать компромисс между точностью и значимостью. Например, предупреждая кого-то о падении к ним предмета, не нужно быть точным о точной массе и скорости.
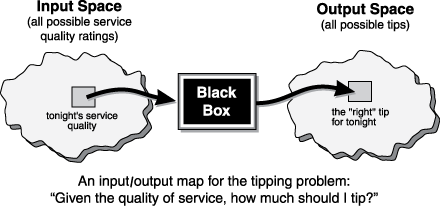
Нечеткая логика является удобным способом отображения входного пространства в выходное пространство. Рассмотрим следующие примеры.
С информацией о том, как хорошо ваш сервис был в ресторане, нечеткая логическая система может сказать вам, что чаевые должны быть.
С Вашей спецификацией того, насколько горячей Вы хотите воду, нечеткая логическая система может настроить клапан крана в нужное положение.
С информацией о том, как далеко находится тема вашей фотографии, нечеткая логическая система может сфокусировать объектив для вас.
С информацией о том, как быстро едет автомобиль и как тяжело работает мотор, нечеткая логическая система может переключать передачи для вас.
Нечеткая система ведет себя как черный ящик, который сопоставляет входное пространство с выходным пространством. Например, можно сопоставить пространство ввода всех возможных рейтингов ресторанного сервиса со всеми возможными значениями чаевых.
Определение соответствующего количества наконечника требует отображения входных сигналов на соответствующие выходные сигналы. Между входом и выходом на предыдущем рисунке показан чёрный ящик, который может содержать любое количество вещей: нечеткие системы, линейные системы, экспертные системы, нейронные сети, дифференциальные уравнения, интерполированные многомерные таблицы поиска или даже духовный советник, лишь бы назвать несколько возможных вариантов. Очевидно, что список может продолжаться и дальше.
Из десятков способов заставить черный ящик работать, оказывается, что нечеткий часто является самым лучшим способом. Почему это должно быть? Как однажды заметил Лотфи Задех, который считается отцом нечеткой логики: «Практически в каждом случае можно построить один и тот же продукт без нечеткой логики, но нечеткая быстрее и дешевле».
Вот список общих наблюдений о нечеткой логике:
Нечеткую логику концептуально легко понять.
Математические понятия, лежащие в основе нечетких рассуждений, очень просты. Нечеткая логика - это более интуитивный подход без далеко идущей сложности.
Нечеткая логика гибкая.
В любой данной системе легко наслаиваться на дополнительные функциональные возможности, не начиная снова с нуля.
Нечеткая логика терпима к неточным данным.
Все неточно, если присмотреться достаточно пристально, но более того, большинство вещей неточны даже при тщательном осмотре. Нечеткие рассуждения выстраивают это понимание в процесс, а не привязывают его к концу.
Нечеткая логика может моделировать нелинейные функции произвольной сложности.
Можно создать нечеткую систему, соответствующую любому набору данных ввода-вывода. Этот процесс особенно прост благодаря адаптивным методам, таким как Adaptive Neuro-Fuzzy Inverence Systems (ANFIS), которые доступны в программном обеспечении Fuzzy Logic Toolbox.
Нечеткая логика может строиться поверх опыта экспертов.
В прямом отличие от нейронных сетей, которые берут обучающие данные и генерируют непрозрачные, непроницаемые модели, нечеткая логика позволяет полагаться на опыт людей, которые уже понимают вашу систему.
Нечеткая логика может быть смешана с обычными методами управления.
Нечеткие системы не обязательно заменяют традиционные методы управления. Во многих случаях нечеткие системы дополняют их и упрощают их реализацию.
Нечеткая логика основана на естественном языке.
Основа нечеткой логики - основа человеческого общения. Это наблюдение лежит в основе многих других утверждений о нечеткой логике. Поскольку нечеткая логика построена на структурах качественного описания, используемых в повседневном языке, нечеткая логика проста в использовании.
Последнее заявление является, пожалуй, самым важным и заслуживает дополнительного обсуждения. Естественный язык, которым ежедневно пользуются простые люди, был сформирован тысячелетней историей человечества, чтобы быть удобным и эффективным. Предложения, написанные на обычном языке, представляют собой триумф эффективного общения.
Нечеткая логика - это не лечение. Когда не следует использовать нечеткую логику? Наиболее безопасным является первое утверждение, сделанное в этом введении: нечеткая логика является удобным способом отображения входного пространства в выходное пространство. Если вы обнаружите, что это не удобно, попробуйте что-нибудь еще. Если более простое решение уже существует, используйте его. Нечеткая логика - кодификация здравого смысла - используйте здравый смысл, когда вы его реализуете и, вероятно, примете правильное решение. Многие контроллеры, например, выполняют прекрасную работу без использования нечеткой логики. Однако, если вам понадобится время, чтобы ознакомиться с нечеткой логикой, вы увидите, что она может быть очень мощным инструментом для быстрого и эффективного решения проблем неточности и нелинейности.
С помощью программного обеспечения Fuzzy Logic Toolbox можно:
Создание и редактирование нечетких систем вывода с помощью функций командной строки или приложения Fuzzy Logic Designer.
Автоматически создавать нечеткие системы с использованием кластеризации или адаптивных нейро-нечетких методов.
Автоматическая настройка параметров нечеткой логической системы с использованием таких методов оптимизации, как генетические алгоритмы и оптимизация роя частиц. Дополнительные сведения см. в разделе Настройка нечетких систем вывода.
Моделирование нечеткой системы в модели Simulink ® с помощью блока контроллера нечеткой логики.
Автоматическое создание кода для оценки нечетких систем вывода. Дополнительные сведения см. в разделе Развертывание нечетких систем вывода.