Точка нечеткой логики состоит в том, чтобы сопоставить входное пространство с выходным пространством, и основным механизмом для этого является список операторов if-then, называемых правилами. Все правила оцениваются параллельно, и порядок правил неважен. Сами правила полезны, поскольку они ссылаются на переменные и прилагательные, описывающие эти переменные. Прежде чем создавать систему, которая интерпретирует правила, необходимо определить все термины, которые вы планируете использовать, и прилагательные, которые их описывают. Чтобы сказать, что вода горячая, необходимо определить диапазон, в котором температура воды может изменяться, а также то, что вы имеете в виду под словом горячая.
В общем, нечеткий вывод - это метод, который интерпретирует значения во входном векторе и, основываясь на некотором наборе правил, присваивает значения выходному вектору.
Этот раздел содержит пошаговое описание процесса нечеткой логики и введение в теорию и практику нечеткой логики.
Нечеткая логика начинается с концепции нечеткого множества. Нечеткое множество - это множество без четкой, четко определенной границы. Он может содержать элементы только с частичной степенью членства.
Чтобы понять, что такое нечеткое множество, сначала рассмотрим определение классического множества. Классический набор - это контейнер, который полностью включает или полностью исключает любой данный элемент. Например, набор дней недели, несомненно, включает понедельник, четверг и субботу. Это так же бесспорно исключает масло, свободу, спинные плавники и так далее.
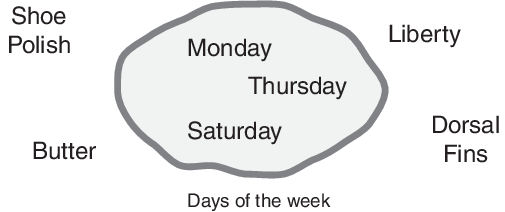
Этот тип множества называется классическим, потому что он существует уже давно. Именно Аристотель впервые сформулировал Закон Исключенного Среднего, в котором говорится, что X должен быть либо в наборе A, либо в наборе not-A. Другой вариант этого закона:
| Что касается любого субъекта, то одно должно быть либо утверждено, либо опровергнуто. |
Чтобы повторить этот закон с аннотациями: «Из любого предмета (скажем, понедельника) одно (день недели) должно быть либо утверждено, либо отклонено (я утверждаю, что понедельник является днем недели)». Этот закон требует, чтобы противоположности, две категории А и не-А, между ними содержали всю вселенную. Все попадает либо в одну группу, либо в другую. Нет ничего, что было бы и днем недели, и не днем недели.
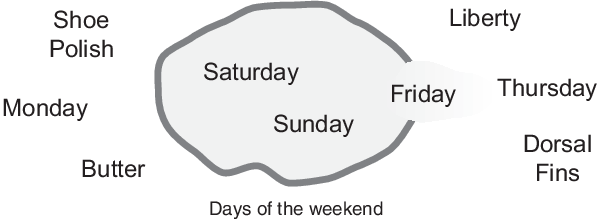
Теперь рассмотрим набор дней, включающий выходные. На следующей диаграмме предпринята попытка классификации выходных дней.
Большинство согласится, что суббота и воскресенье относятся к выходным, но как насчет пятницы? Такое ощущение, что это часть уик-энда, но как-то кажется, что это должно быть технически исключено. Поэтому пятница «переступает забор». Классические наборы не переносят такого рода классификацию. Либо что-то находится в наборе, либо находится вне набора. Однако человеческий опыт говорит о том, что пересечение забора - это часть жизни.
Конечно, индивидуальные представления и культурный фон должны учитываться, когда вы определяете, что составляет выходные. Даже словарь неточен, определяя выходные как период с вечера пятницы или субботы до утра понедельника. Вы входите в область, где резкая, да-нет логика перестает быть полезной. Нечеткие рассуждения становятся ценными именно тогда, когда вы работаете с тем, как люди на самом деле воспринимают концептуальные выходные в отличие от простодушной классификации, полезной только для целей бухгалтерского учета. Больше всего на свете следующее утверждение закладывает основы нечеткой логики.
| В нечеткой логике истинность любого утверждения становится вопросом степени. |
Любой оператор может быть нечетким. Главное преимущество, которое предлагает нечеткое рассуждение, - это возможность ответить на вопрос «да-нет» с ответом «не совсем да» или «нет». Люди делают такие вещи постоянно (подумайте, как редко вы получаете прямой ответ на, казалось бы, простой вопрос), но это довольно новый трюк для компьютеров.
Как это работает? Рассуждение в нечеткой логике - это просто вопрос обобщения знакомой логики yes-no (Boolean). Если вы даете true числовое значение 1 и false числовое значение 0, это значение указывает на то, что нечеткая логика также позволяет между значениями 0,2 и 0,7453. Например:
| В: Суббота - выходной день? |
| A: 1 (да или правда) |
| В: Вторник - выходной день? |
| A: 0 (нет или ложь) |
| В: Пятница - выходной день? |
| A: 0.8 (по большей части да, но не полностью) |
| В: Воскресенье - выходной день? |
| О: 0,95 (да, но не так сильно, как в субботу). |
График слева показывает истинные значения для weekend-ness, если вы вынуждены отвечать абсолютным «да» или «нет». Справа - график, который показывает истинное значение для weekend-ness, если вам разрешено отвечать нечеткими значениями между ними.
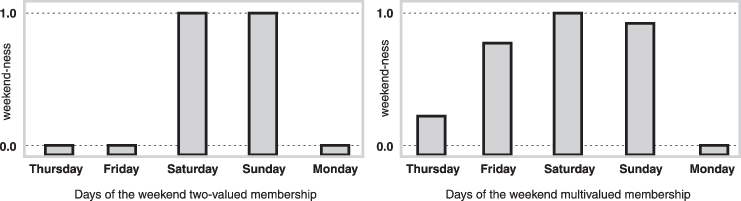
Технически представление справа происходит из области многозначной логики (или многозначной логики). Если задать вопрос «Является ли X членом набора A?», ответ может быть да, нет или любое одно из тысячи промежуточных значений между ними. Таким образом, X может иметь частичное членство в A. Многозначная логика находится в прямом контрасте с более привычным понятием двузначной (или двухвалентной «да-нет») логики.
Чтобы вернуться к примеру, рассмотрим график непрерывного масштабного времени выходного дня, показанный на следующих графиках.
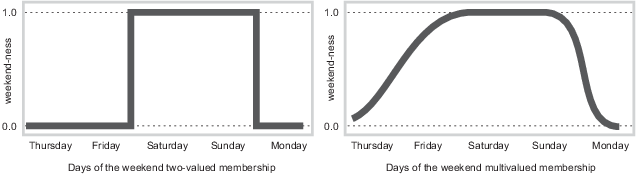
Делая график непрерывным, вы определяете степень, в которой любой данный момент принадлежит в выходные, а не целый день. В сюжете слева обратите внимание, что в полночь в пятницу, так же как вторая рука проносится за 12, истинное значение выходного дня скачкообразно скачет от 0 до 1. Это один из способов определения выходного дня, и хотя он может быть полезен бухгалтеру, он может не действительно связываться с вашим реальным опытом выходного дня.
График справа показывает плавно изменяющуюся кривую, которая объясняет тот факт, что вся пятница, и, в небольшой степени, части четверга, принимают качество выходного дня и, таким образом, заслуживают частичного участия в нечетком наборе моментов выходного дня. Кривая, определяющая выходные дни любого момента времени, является функцией, которая отображает входное пространство (время недели) в выходное пространство (выходные дни). В частности, она известна как функция членства. Более подробное обсуждение см. в разделе Функции членства.
В качестве другого примера нечетких наборов рассмотрим вопрос о сезонах. Какой сейчас сезон? В северном полушарии лето официально начинается в тот самый момент земной орбиты, когда Северный полюс направлен наиболее непосредственно к Солнцу. Происходит ровно раз в год, в конце июня. Используя астрономические определения для сезона, вы получите острые границы, как показано слева на следующем рисунке. Но то, что вы испытываете, когда сезоны меняются более или менее непрерывно, как показано справа на следующем рисунке (в климате умеренного северного полушария).
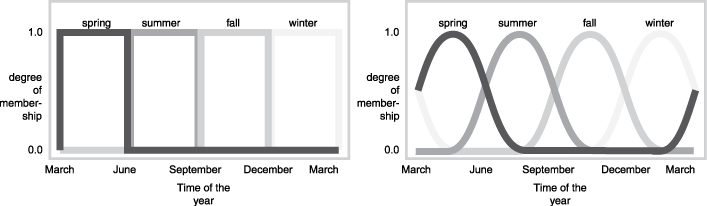
Функция членства (MF) - это кривая, которая определяет, как каждая точка во входном пространстве отображается на значение членства (или степень членства) между 0 и 1. Пространство ввода иногда называют вселенной дискурса, модным названием для простого понятия.
Одним из наиболее часто используемых примеров нечеткого набора является набор высоких людей. В этом случае вселенная дискурса - это все потенциальные высоты, скажем, от трех футов до девяти футов, и слово «высокий» соответствовало бы кривой, которая определяет степень роста любого человека. Если множеству высоких людей дана четко определенная (четкая) граница классического множества, можно сказать, что все люди выше шести футов официально считаются высокими. Однако такое различие явно абсурдно. Возможно, имеет смысл рассматривать множество всех реальных чисел больше шести, потому что числа принадлежат абстрактной плоскости, но когда мы хотим говорить о реальных людях, неразумно называть одного человека коротким, а другого высоким, когда они отличаются ростом на ширину волос.

Если ранее показанное различие неработоспособно, то как правильно определить набор высоких людей? Как и на графике выходных дней, на рисунке ниже показана плавно изменяющаяся кривая, которая переходит от невысокого к высокому. Выходная ось - это число, называемое значением членства в диапазоне от 0 до 1. Кривая известна как функция членства и часто дается обозначение µ. Например, на следующем рисунке показаны как четкие, так и плавные высокие функции членства. В топовом сюжете два человека классифицируются как либо полностью высокие, либо полностью невысокие. На нижнем графике плавный переход допускает различные степени высоты. Оба человека в какой-то степени высокие, но один значительно менее высокий, чем другой. Более высокий человек, с высоким членством 0,95 определенно высокий человек, но человек с высоким членством 0,3 не очень высокий.
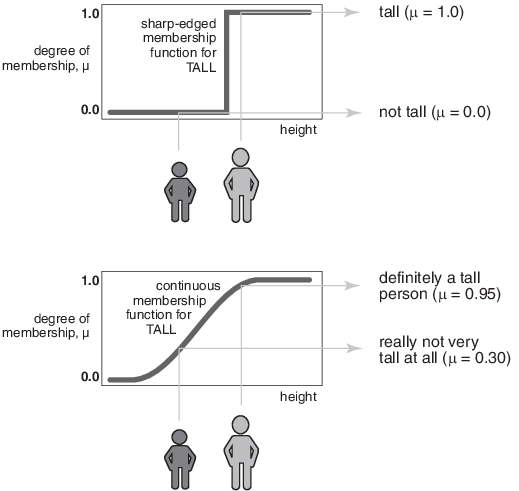
Субъективные интерпретации и соответствующие единицы встроены прямо в нечеткие множества. Если вы говорите «Она высокая», функция членства должна уже учитывать, имеете ли вы в виду шестилетнюю или взрослую женщину. Аналогично, единицы измерения включаются в кривую. Конечно, нет смысла говорить «Она высокая в дюймах или в метрах?»
Единственное условие, которому должна удовлетворять функция членства, это то, что она должна варьироваться от 0 до 1. Сама функция может быть произвольной кривой, форму которой мы можем определить как функцию, которая подходит нам с точки зрения простоты, удобства, скорости и эффективности.
Классическое множество может быть выражено как
> 6}
Нечеткое множество - это расширение классического множества. Если X - вселенная дискурса и её элементы обозначаются х, то нечеткое множество A в X определяется как множество упорядоченных пар.
|x∈X}
| A = {x, мкА (x) | x ∈ X} |
(x) называется функцией членства (или MF) x в A. Функция членства отображает каждый элемент X в значение членства между 0 и 1.
Панель инструментов включает 11 встроенных типов функций членства. Эти 11 функций, в свою очередь, построены из нескольких основных функций:
Линейные функции по частям
Гауссова функция распределения
Сигмоидная кривая
Квадратичные и кубические полиномиальные кривые
Для получения подробной информации о любой из перечисленных ниже функций членства см. соответствующую справочную страницу.
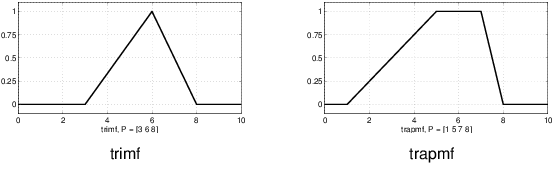
Простейшие функции членства формируются с помощью прямых линий. Из них самым простым является треугольная функция членства, и она имеет имя функции trimf. Эта функция - не что иное, как совокупность трёх точек, образующих треугольник. Трапециевидная функция членства, trapmf, имеет плоский верх и действительно является просто усеченный треугольник кривой. Эти прямые функции членства имеют преимущество простоты.
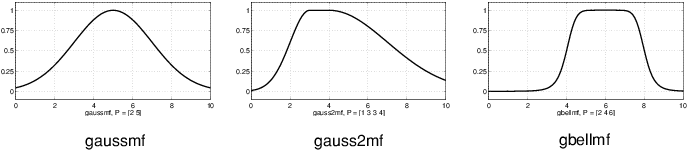
На кривой гауссова распределения построены две функции членства: простая гауссова кривая и двусторонний композит из двух различных гауссовых кривых. Две функции: gaussmf и gauss2mf.
Обобщенная функция членства колокола задана тремя параметрами и имеет имя функции gbellmf. Функция членства колокола имеет на один параметр больше, чем функция членства Гаусса, поэтому она может приблизиться к нечеткому набору, если свободный параметр настроен. Из-за их гладкости и краткости обозначения, гауссовы и колокольные функции членства являются популярными методами для указания нечетких множеств. Обе эти кривые имеют преимущество быть гладкими и ненулевыми во всех точках.
Хотя функции членства Гаусса и функции членства колокола достигают гладкости, они не могут указать асимметричные функции членства, которые важны в некоторых приложениях. Далее определяется сигмоидальная функция членства, которая открыта слева или справа. Асимметричные и замкнутые (т.е. не открытые слева или справа) функции членства могут быть синтезированы с помощью двух сигмоидальных функций, поэтому в дополнение к основным sigmf, вы также имеете разницу между двумя сигмоидальными функциями, dsigmfи произведение двух сигмоидальных функций psigmf.
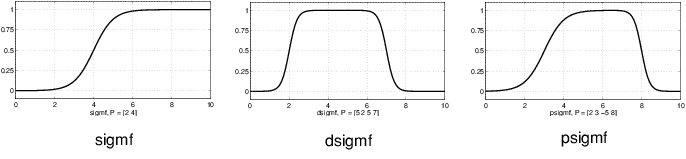
Кривые на основе полиномов составляют несколько функций членства на панели инструментов. Три связанные функции членства являются кривыми Z, S и Pi, все названы из-за их формы. Функция zmf - асимметричная полиномиальная кривая, открытая слева, smf функция зеркального отображения, которая открывается справа, и pimf равен нулю на обеих крайностях с подъемом посередине.
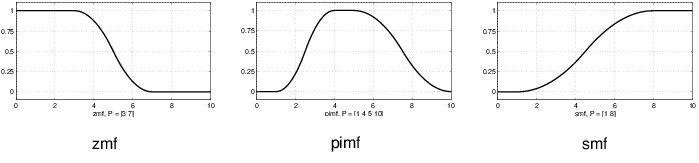
Существует очень широкий выбор для выбора при выборе функции членства. С помощью панели инструментов можно также создать собственные функции членства. Однако, если список, основанный на расширенных функциях членства, кажется слишком сложным, просто помните, что вы, вероятно, могли бы очень хорошо ладить только с одним или двумя типами функций членства, например треугольник и трапециевидные функции. Выбор широк для тех, кто хочет изучить возможности, но расширительные функции членства не нужны для хороших нечетких систем вывода. Наконец, следует помнить, что более подробная информация обо всех этих функциях содержится в ссылочном разделе.
Нечеткие наборы описывают расплывчатые понятия (например, быстрый бегун, жаркая погода, выходные дни).
Нечеткий набор допускает возможность частичного членства в нём. (например, пятница - это своего рода выходной день, погода довольно жаркая).
Степень принадлежности объекта нечеткому множеству обозначается значением членства в диапазоне от 0 до 1 (например, пятница является выходным днем в степени 0,8).
Функция членства, связанная с данным нечетким набором, отображает входное значение в соответствующее ей значение членства.
Теперь, когда вы понимаете нечеткий вывод, вы должны увидеть, как нечеткий вывод связан с логическими операциями.
Самое главное, что нужно осознать о нечетком логическом рассуждении, - это тот факт, что это суперсеть стандартной булевой логики. Другими словами, если оставить нечеткие значения в их крайних значениях 1 (полностью истина) и 0 (полностью ложь), стандартные логические операции сохранятся. В качестве примера рассмотрим следующие стандартные таблицы истинности.
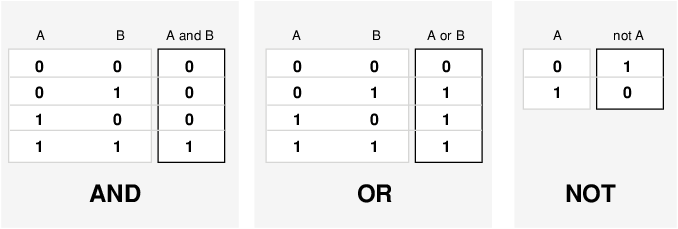
Учитывая, что в нечеткой логике истинность любого утверждения является вопросом степени, могут ли эти таблицы истинности быть изменены? Входные значения могут быть вещественными числами от 0 до 1. Какая функция сохраняет результаты таблицы истинности AND (например), а также распространяется на все вещественные числа от 0 до 1?
Одним из ответов является операция min. То есть разрешить оператор A AND B, где A и B ограничены диапазоном (0,1), используя функцию min (A, B). Используя те же рассуждения, можно заменить операцию OR функцией max, так что A OR B становится эквивалентным max (A, B). Наконец, операция NOT A становится эквивалентной 1 − A. Предыдущая таблица истинности полностью неизменна этой заменой.
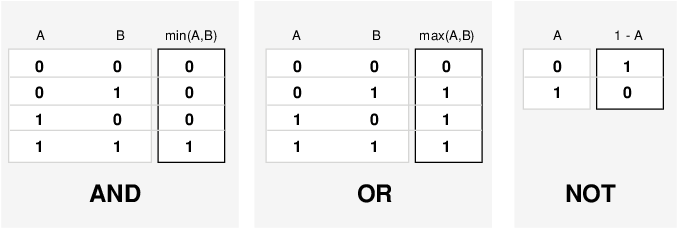
Кроме того, поскольку за таблицей истинности стоит функция, а не только сама таблица истинности, теперь можно рассматривать значения, отличные от 1 и 0.
На следующем рисунке для отображения той же информации используется график. На этом рисунке таблица истинности преобразуется в график из двух нечетких наборов, применяемых вместе для создания одного нечеткого набора. В верхней части рисунка отображаются графики, соответствующие предыдущим двузначным таблицам истинности, в то время как в нижней части рисунка показано, как операции работают в непрерывно изменяющемся диапазоне значений истинности A и B в соответствии с определенными нечеткими операциями.
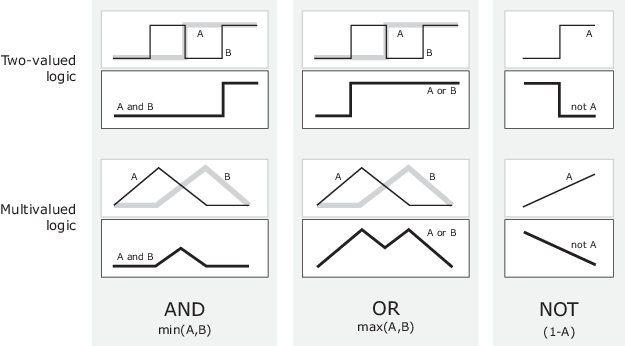
Учитывая эти три функции, можно разрешить любую конструкцию с помощью нечетких наборов и нечеткой логической операции AND, OR и NOT.
В этом случае определено только одно конкретное соответствие между двузначными и многозначными логическими операциями для AND, OR и NOT. Эта переписка отнюдь не уникальна.
В более общих чертах, вы определяете то, что известно как нечеткое пересечение или объединение (AND), нечеткое объединение или дизъюнкция (OR) и нечеткое дополнение (NOT). Классическими операторами для этих функций являются: AND = min, OR = max, и NOT = аддитивное дополнение. Обычно большинство приложений с нечеткой логикой используют эти операции и оставляют их при этом. Однако в целом эти функции являются произвольными в удивительной степени. Программное обеспечение Fuzzy Logic Toolbox™ использует классический оператор для нечеткого дополнения, как показано на предыдущем рисунке, но также позволяет настраивать операторы AND и OR.
Пересечение двух нечетких множеств A и B определяется, в общем, двоичным отображением T, которое агрегирует две функции членства следующим образом:
мкВ (x))
Например, двоичный оператор Т может представлять умножение мкА (x) и мкВ (x). Эти операторы нечеткого пересечения, которые обычно называются операторами T-norm (треугольная норма), удовлетворяют следующим основным требованиям:
Оператор T-norm - это двоичное отображение T (.,.) со следующими свойствами:
Граница - (1, a) = a
Монотонность - c, dесли a≤c и b≤d
Коммутативность - (b, a)
Ассоциативность - (a, b), c)
Первое требование накладывает правильное обобщение на хрустящие множества. Второе требование подразумевает, что уменьшение значений членства в A или B не может привести к увеличению значения членства в A пересечении B. Третье требование указывает, что оператор безразличен к порядку нечетких наборов, подлежащих объединению. Наконец, четвёртое требование позволяет взять пересечение любого числа множеств в любом порядке парных группировок.
Как и нечеткое пересечение, оператор нечеткого объединения обычно задается двоичным отображением S:
мкВ (x))
Например, бинарный оператор S может представлять собой добавление мкА (x) и мкВ (x). Эти операторы нечеткого объединения, которые часто называют операторами T-conorm (или S-нормой), должны удовлетворять следующим основным требованиям:
Оператор T-conorm (или S-норма) - это двоичное отображение S (.,.) со следующими свойствами:
Граница - (0, a) = a
Монотонность - c, dесли a≤c и b≤d
Коммутативность - (b, a)
Ассоциативность - (a, b), c)
В прошлом было предложено несколько параметризованных T-норм и двойственных T-конвормов, таких как Yager [11], Dubois и Prade [1], Schweizer и Sklar [8] и Sugeno [9]. Каждый из них обеспечивает способ изменения коэффициента усиления функции так, чтобы он мог быть очень ограничительным или очень разрешительным.
Нечёткие множества и нечёткие операторы являются сюжетами и глаголами нечёткой логики. Эти операторы if-then используются для формулирования условных операторов, которые содержат нечеткую логику.
Одно нечеткое правило if-then принимает вид
| Если x - A, то y - B |
где A и B - лингвистические значения, определяемые нечеткими множествами в диапазонах (вселенных дискурса) X и Y соответственно. if-часть правила «x is A» называется предшествующим или предполагаемым, тогда как then-часть правила «y is B» называется последующим или выводом. Примером такого правила может быть
| Если обслуживание хорошее, то чаевые средние |
Понятие good представлено в виде числа между 0 и 1, и, таким образом, предшествующая интерпретация возвращает одно число между 0 и 1. И наоборот, среднее значение представляется как нечеткое множество, и, следовательно, результатом является назначение, которое назначает все нечеткое множество B выходной переменной y. В правиле if-then слово употребляется двумя совершенно разными способами в зависимости от того, появляется ли оно в предшествующем или последующем. В терминах MATLAB ® это различие между реляционным тестом с использованием «= =» и присвоением переменной с использованием символа «=». Менее запутанным способом написания правила было бы
| Если обслуживание = хорошее, то совет = среднее значение |
В общем случае, вход в правило if-then является текущим значением для входной переменной (в данном случае услуги), а выход является целым нечетким набором (в данном случае средним). Этот набор будет впоследствии определен по умолчанию, назначив выходному сигналу одно значение. Концепция дефузификации описана в следующем разделе.
Интерпретация правила if-then включает два шага:
Оценка предшествующего периода - нечеткость входных данных и применение любых необходимых нечетких операторов.
Применение результата к последнему.
Второй этап известен как импликация. Для правила if-then, антецедент, p, подразумевает последующее, q. В двоичной логике, если p равно true, то q также равно true (p → q). В нечеткой логике, если p верен до некоторой степени членства, то q также верен до той же степени (0.5p → 0.5q). В обоих случаях, если p имеет значение false, то значение q не определено.
Предшествующий элемент правила может иметь несколько частей.
| Если небо серое и ветер сильный и барометр падает, то... |
В этом случае все части предшествующего кода вычисляются одновременно и преобразуются в одно число с помощью логических операторов, описанных в предыдущем разделе. Результат правила также может иметь несколько частей.
| Если температура холодная, то клапан горячей воды открыт, а клапан холодной воды закрыт |
В этом случае на все последующие последствия в равной степени влияет результат предшествующего события. Как на результат влияет предшествующий? Последующий задает нечеткий набор, назначаемый выходному сигналу. Затем функция импликации изменяет нечеткий набор на степень, заданную предшествующим значением. Наиболее распространенными способами изменения выходного нечеткого набора являются усечение с помощью min функция (где нечеткий набор усечен, как показано на следующем рисунке) или масштабирование с помощью prod (где выходной нечеткий набор сдвинут). Оба элемента поддерживаются панелью инструментов, но для примеров в этом разделе используется усечение.
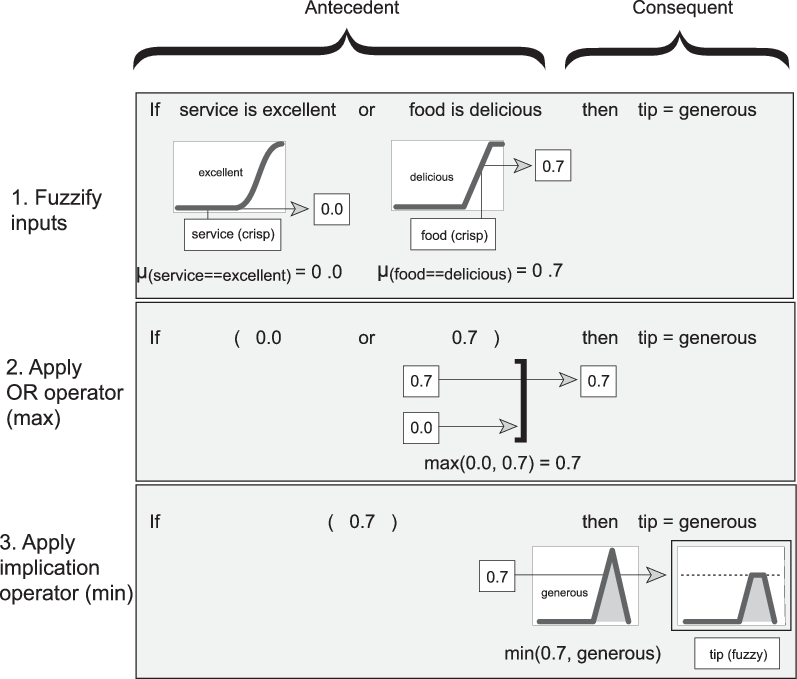
Интерпретация правил if - это процесс из трех частей. Этот процесс подробно описан в следующем разделе:
Нечеткие входные данные: разрешите все нечеткие операторы в предшествующем периоде до степени членства в диапазоне от 0 до 1. Если есть только одна часть к антецеденту, то это степень поддержки правила.
Применить оператор нечеткости к нескольким антецедентам деталей: Если к антецеденту имеется несколько частей, примените операторы нечеткой логики и разрешите антецедент в одно число от 0 до 1. Это степень поддержки правила.
Метод Apply implication: Используйте степень поддержки для всего правила, чтобы сформировать выходной нечеткий набор. Результат действия нечеткого правила назначает весь нечеткий набор выходному сигналу. Это нечеткое множество представлено функцией членства, которая выбрана для указания качеств последующего. Если предшествующее значение является только частично истинным (т.е. ему присваивается значение меньше 1), то выходное нечеткое множество усекается согласно методу импликации.
В целом одно правило неэффективно. Необходимы два или более правил, которые могут играть друг с другом. Выходные данные каждого правила являются нечетким набором. Выходные нечеткие наборы для каждого правила затем объединяются в один выходной нечеткий набор. Наконец, результирующий набор дефузизируется или преобразуется в одно число. Построение нечетких систем с использованием конструктора нечеткой логики показывает, как весь процесс работает от начала до конца для определенного типа системы нечеткого вывода, называемой типом Мамдани.
[1] Дюбуа, Дидье и Анри М. Праде. Нечеткие наборы и системы: теория и приложения. Математика в науке и технике, ст. 144. Нью-Йорк: Академическая пресса, 1980.
[2] Кауфманн, А. и Мадан М. Гупта. Введение в нечеткую арифметику: теория и приложения. Van Nostrand Reinold Electrical/Computer Science and Engineering Series. Нью-Йорк, Нью-Йорк: Van Nostrand Reinhold Co, 1985.
[3] Lee, C.C. "Нечеткая логика в системах управления: контроллер нечеткой логики. I. " Транзакции IEEE по системам, человеку и кибернетике 20, № 2 (апрель 1990): 404-18. https://doi.org/10.1109/21.52551.
[4] Lee, C.C. "Нечеткая логика в системах управления: контроллер нечеткой логики. II ". IEEE Transactions on Systems, Man, and Cybernetics 20, No 2 (April 1990): 419-35. https://doi.org/10.1109/21.52552.
[5] Мамдани, Э. Х. и С. Ассилиан. «Эксперимент в лингвистическом синтезе с нечетким логическим контроллером». Международный журнал человеко-машинных исследований 7, № 1 (январь 1975 года): 1-13. https://doi.org/10.1016/S0020-7373 (75) 80002-2.
[6] Мамдани, Э. Х. «Достижения в лингвистическом синтезе нечетких контроллеров». Международный журнал человеко-машинных исследований 8, № 6 (ноябрь 1976 года): 669-78. https://doi.org/10.1016/S0020-7373 (76) 80028-4.
[7] Мамдани, Е. Х. «Применение нечеткой логики для аппроксимации рассуждений с использованием лингвистического синтеза». IEEE Transactions on Computers C-26, No 12 (декабрь 1977): 1182-91. https://doi.org/10.1109/TC.1977.1674779.
[8] Швайзер, Б. и А. Склар, «Ассоциативные функции и абстрактные полугруппы». Публик. Мат. Дебрецен 10 (1963): 69-81.
[9] Сугено, М., «Нечеткие меры и нечеткие интегралы: обзор», (М. М. Гупта, Г. Н. Саридис, и Б. Р. Гейнс, редакторы) Нечеткие автоматы и процессы принятия решений, стр. 89-102, Северо-Голландия, Нью-Йорк, 1977.
[10] Sugeno, Michio, ред. Промышленные применения нечеткого контроля. Амстердам; Нью-Йорк: Нью-Йорк, Нью-Йорк, США: Северная Голландия; Единственный дистрибьютор в США и Канаде, Elsevier Science Pub. Ко, 1985.
[11] Ягер, Рональд Р. «Об общем классе нечетких соединителей». Нечеткие наборы и системы 4, № 3 (ноябрь 1980): 235-42. https://doi.org/10.1016/0165-0114 (80) 90013-5.
[12] Ягер, Рональд Р. и Димитр П. Филев. «Генерация нечетких правил горной кластеризацией». Журнал интеллектуальных и нечетких систем 2, № 3 (1994): 209-19. https://doi.org/10.3233/IFS-1994-2301.
[13] Заде, Л.А. «Нечеткие наборы». Информация и контроль 8, № 3 (июнь 1965): 338-53. https://doi.org/10.1016/S0019-9958 (65) 90241-X.
[14] Заде, Лотфи А. «Наброски нового подхода к анализу сложных систем и процессов принятия решений». Транзакции IEEE по системам, человеку и кибернетике SMC-3, № 1 (1973): 28-44. https://doi.org/10.1109/TSMC.1973.5408575.
[15] Заде, Л.А. 'Понятие лингвистической переменной и ее применение к приблизительным рассуждениям. I '.Информационные науки 8, № 3 (1975): 199-249. https://doi.org/10.1016/0020-0255 (75) 90036-5
[16] Заде, Л.А. 'Понятие лингвистической переменной и ее применение к приблизительным рассуждениям. II '. 8 информационных наук, № 4 (1975): 301-357. https://doi.org/10.1016/0020-0255 (75) 90046-8
[17] Заде, Л.А. 'Понятие лингвистической переменной и ее применение к приблизительным рассуждениям. III '. 9 информационных наук, № 1 (1975): 43-80. https://doi.org/10.1016/0020-0255 (75) 90017-1
[18] Заде, Л.А. «Нечеткая логика». Компьютер 21, № 4 (апрель 1988): 83-93. https://doi.org/10.1109/2.53.
[19] Заде, Л.А. «Представление знаний в нечеткой логике». IEEE Транзакции в области знаний и разработки данных 1, № 1 (март 1989 года): 89-100. https://doi.org/10.1109/69.43406.