GlobalSearch и MultiStart имеют сходные подходы к поиску глобальных или множественных минимумов. Оба алгоритма запускают локальный решатель (например, fmincon) из нескольких начальных точек. Алгоритмы используют несколько начальных точек для выборки нескольких бассейнов притяжения. Дополнительные сведения см. в разделе Бассейны притяжения.
В разделе «Обзор алгоритма, выполняющего поиск и мультизапуск» содержится эскиз GlobalSearch и MultiStart алгоритмы.
GlobalSearch и обзор алгоритма MultiStart
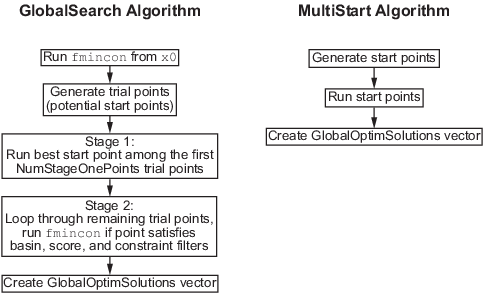
Основные различия между GlobalSearch и MultiStart являются:
GlobalSearch использует механизм поиска рассеяния для формирования начальных точек. MultiStart использует равномерно распределенные начальные точки в пределах границ или заданные пользователем начальные точки.
GlobalSearch анализирует начальные точки и отклоняет те точки, которые вряд ли улучшат лучший локальный минимум, найденный на данный момент. MultiStart запускает все начальные точки (или, при необходимости, все начальные точки, которые являются возможными по отношению к ограничениям или ограничениям неравенства).
MultiStart дает выбор локального решателя: fmincon, fminunc, lsqcurvefit, или lsqnonlin. GlobalSearch использование алгоритма fmincon.
MultiStart может выполняться параллельно, распределяя начальные точки на несколько процессоров для локального решения. Бежать MultiStart параллельно см. раздел Использование параллельной обработки в инструментарии глобальной оптимизации.
Различия между этими объектами решателя сводятся к следующему решению относительно использования:
Использовать GlobalSearch найти один глобальный минимум наиболее эффективно на одном процессоре.
Использовать MultiStart кому:
Найти несколько локальных минимумов.
Бегите параллельно.
Использовать решатель, отличный от fmincon.
Выполните тщательный поиск глобального минимума.
Изучите собственные начальные точки.
Описание алгоритма см. в Ugray et al. [1].
Когда вы run a GlobalSearch , алгоритм выполняет следующие шаги:
GlobalSearch пробеги fmincon от начальной точки, которую вы даете в problem структура. Если этот прогон сходится, GlobalSearch записывает начальную и конечную точки для первоначальной оценки радиуса бассейна притяжения. Кроме того, GlobalSearch записывает конечное значение целевой функции для использования в функции оценки (см. Получение начальной точки этапа 1, прогон).
Функция оценки - это сумма значения целевой функции в точке и кратная сумме нарушений ограничения. Таким образом, достижимая точка имеет оценку, равную ее значению целевой функции. Число для нарушений ограничения первоначально равно 1000. GlobalSearch обновляет несколько во время выполнения.
GlobalSearch использует алгоритм поиска рассеяния для генерации набора NumTrialPoints пробные пункты. Пробные точки - это потенциальные начальные точки. Описание алгоритма поиска рассеяния см. в разделе Glover [2]. GlobalSearch генерирует пробные точки в пределах любых заданных конечных границ (lb и ub). Неограниченные компоненты имеют искусственные границы: lb = -1e4 + 1, ub = 1e4 + 1. Этот диапазон не симметричен относительно начала координат, так что начало координат не находится в поиске рассеяния. Компоненты с односторонними границами имеют искусственные границы, наложенные на неограниченную сторону, сдвинутые на конечные границы для сохранения lb < ub.
GlobalSearch оценивает функцию оценки набора NumStageOnePoints пробные пункты. Затем набирает очко с лучшим баллом и бежит fmincon с этого момента. GlobalSearch удаляет набор NumStageOnePoints пробные точки из своего списка точек для изучения.
localSolverThreshold первоначально является меньшим из двух значений целевой функции в точках решения. Точки решения: fmincon решения, начиная с x0 и от начальной точки этапа 1. Если обе эти точки решения не существуют или являются неосуществимыми, localSolverThreshold первоначально является значением штрафной функции начальной точки этапа 1.
GlobalSearch эвристическое предположение состоит в том, что бассейны притяжения сферические. Первоначальная оценка бассейнов притяжения для точки решения от x0 и точка раствора со стадии 1 являются сферами, центрированными в точках раствора. Радиус каждой сферы - это расстояние от начальной точки до точки решения. Эти расчетные бассейны могут перекрываться.
Существует два набора счетчиков, связанных с алгоритмом. Каждый счетчик - это количество последовательных пробных точек, которые:
Лежите в бассейне притяжения. На каждый бассейн приходится по одному счетчику.
Иметь функцию оценки больше, чем localSolverThreshold. Определение оценки см. в разделе Запуск fmincon из x0.
Все счетчики изначально равны 0.
GlobalSearch повторно проверяет оставшуюся пробную точку из списка и выполняет следующие действия. Он постоянно отслеживает время и останавливает поиск, если истекшее время превышает MaxTime секунд.
Вызов пробной точки p. Управляемый fmincon от p при соблюдении следующих условий:
p отсутствует ни в одном существующем бассейне. Критерий для каждого бассейна i является:
|p - center(i)| > DistanceThresholdFactor * radius(i).
DistanceThresholdFactor является опцией (значение по умолчанию 0.75).
radius - это расчетный радиус, который обновляется в полях «Обновить радиус и порог бассейна» и «Отреагировать на значения больших счетчиков».
оценка (p) < localSolverThreshold.
(необязательно) p удовлетворяет связанным ограничениям и/или ограничениям неравенства. Этот тест выполняется при установке StartPointsToRun имущества GlobalSearch объект в 'bounds' или 'bounds-ineqs'.
Сброс счетчиков
Установите счетчики для бассейнов и пороговое значение 0.
Обновить набор решений
Если fmincon прогоны, начиная с p, он может дать положительный флаг выхода, который указывает на сходимость. В этом случае GlobalSearch обновляет вектор GlobalOptimSolution объекты. Вызов точки решения xp и значение целевой функции fp. Существует два случая:
Для каждой другой точки решения xq со значением целевой функции fq,
|xq - xp| > XTolerance * max(1,|xp|)
или
|fq - fp| > FunctionTolerance * max(1,|fp|).
В этом случае GlobalSearch создает новый элемент в векторе GlobalOptimSolution объекты. Для получения подробной информации, содержащейся в каждом объекте, см. GlobalOptimSolution.
Для другой точки решения xq со значением целевой функции fq,
|xq - xp| <= XTolerance * max(1,|xp|)
и
|fq - fp| <= FunctionTolerance * max(1,|fp|).
В этом случае GlobalSearch с уважением xp как эквивалент xq. GlobalSearch алгоритм изменяет GlobalOptimSolution из xq путем добавления p в массив ячеек X0 точки.
Есть один незначительный сдвиг, который может произойти с этим обновлением. Если флаг выхода для xq больше, чем 1и флаг выхода для xp является 1, то xp заменяет xq. Эта замена может привести к тому, что некоторые точки в одном и том же бассейне будут больше, чем расстояние XTolerance от xp.
Обновить радиус и порог бассейна
Если флаг выхода текущего fmincon прогон положительный:
Установить пороговое значение оценки в начальной точке p.
Задать радиус бассейна для xp равно максимуму существующего радиуса (если имеется) и расстоянию между p и xp.
Отчет для итеративного просмотра
Когда GlobalSearch Display свойство - 'iter', каждый момент, который fmincon участки создает одну линию в GlobalSearch итеративный дисплей.
Обновить счетчики
Приращение счетчика для каждого бассейна, содержащего p. Сбросить счетчик каждого другого бассейна на 0.
Приращение порогового счетчика, если оценка (p) >= localSolverThreshold. В противном случае сбросьте значение счетчика на 0.
Реагировать на значения больших счетчиков
Для каждого бассейна со счетчиком, равным MaxWaitCycle, умножить радиус бассейна на 1 – BasinRadiusFactor. Сбросить счетчик на 0. (Оба MaxWaitCycle и BasinRadiusFactor являются настраиваемыми свойствами GlobalSearch объект.)
Если пороговый счетчик равен MaxWaitCycle, увеличить пороговое значение:
новое пороговое значение = пороговое значение + PenaltyThresholdFactor*(1 + abs (пороговое значение)).
Сбросить счетчик на 0.
Отчет для итеративного просмотра
Каждая 200-я пробная точка создает одну линию в GlobalSearch итеративный дисплей.
После достижения MaxTime секунды или отсутствие пробных точек, GlobalSearch создает вектор GlobalOptimSolution объекты. GlobalSearch упорядочивает вектор по значению целевой функции, от самого низкого (лучший) до самого высокого (худший). На этом алгоритм завершается.
Когда вы run a MultiStart , алгоритм выполняет следующие шаги:
MultiStart проверяет действительность входных аргументов. Проверки включают однократное выполнение локального решателя на входах проблем. Даже при параллельном выполнении, MultiStart выполняет эти проверки последовательно.
При звонке MultiStart с синтаксисом
[x,fval] = run(ms,problem,k)
для целого числа k, MultiStart производит k - 1 начальные точки точно так же, как если бы вы использовали RandomStartPointSet объект. Алгоритм также использует x0 начальная точка от problem структура, в общей сложности k начальные точки.
A RandomStartPointSet не имеет точек, сохраненных внутри объекта. Вместо этого MultiStart требования list, которая генерирует случайные точки в пределах границ, заданных problem структура. Если существует неограниченный компонент, list использует искусственную связь, заданную ArtificialBound имущества RandomStartPointSet объект.
Если вы предоставляете CustomStartPointSet объект, MultiStart не создает начальные точки, но использует точки в объекте.
Если установить StartPointsToRun имущества MultiStart объект в 'bounds' или 'bounds-ineqs', MultiStart не запускает локальный решатель из неосуществимых начальных точек. В этом контексте «неосуществимые» означают начальные точки, которые не удовлетворяют границам, или начальные точки, которые не удовлетворяют ограничениям как границ, так и неравенства.
Установка по умолчанию для StartPointsToRun является 'all'. В этом случае MultiStart не отбрасывает неосуществимые начальные точки.
MultiStart запускает локальный решатель, указанный в problem.solver, начиная с точек, которые проходят StartPointsToRun фильтр. Если MultiStart работает параллельно, отправляет начальные точки рабочим процессорам по одному, а рабочие процессоры запускают локальный решатель.
Локальный решатель проверяет, MaxTime секунды истекли при каждой итерации. Если это так, она выходит из этой итерации, не сообщая о решении.
Когда локальный решатель останавливается, MultiStart сохраняет результаты и переходит к следующему шагу.
Отчет для итеративного просмотра. Когда MultiStart Display свойство - 'iter', каждая точка, которую запускает локальный решатель, создает одну линию в MultiStart итеративный дисплей.
MultiStart останавливается, когда заканчиваются начальные точки. Он также останавливается, когда превышает общее время выполнения MaxTime секунд.
После MultiStart достигает условия остановки, алгоритм создает вектор GlobalOptimSolution объекты следующим образом:
Сортировать локальные решения по значению целевой функции (Fval) от самого низкого до самого высокого. Для lsqnonlin и lsqcurvefit локальные решатели, целевая функция - норма остатка.
Закольцовывание локальных решений j начиная с самого низкого (лучший) Fval.
Найти все решения k удовлетворяя обоим требованиям:
|Fval(k) - Fval(j)| <= FunctionTolerance*max(1,|Fval(j)|)
|x(k) - x(j)| <= XTolerance*max(1,|x(j)|)
Отчет j, Fval(j), локальный решатель output структура для jи массив ячеек начальных точек для j и все k. Удалить эти точки k из списка локальных решений. Эта точка является одной записью в векторе GlobalOptimSolution объекты.
Результирующий вектор GlobalOptimSolution объекты упорядочены по Fval, от самого низкого (лучший) до самого высокого (худший).
Отчет для итеративного просмотра. Изучив все локальные решения, MultiStart дает сводку для итеративного отображения. Эта сводка включает количество сходящихся локальных прогонов решателя, число неудачных сходящихся прогонов и число ошибок.
[1] Угрей, Зсолт, Леон Ласдон, Джон К. Пламмер, Фред Гловер, Джеймс Келли и Рафаэль Марти. Spatter Search and Local NLP Solvers: Многозаходная структура для глобальной оптимизации. INFORMS Journal on Computing, том 19, № 3, 2007, стр. 328-340.
[2] Гловер, Ф. «Шаблон для поиска рассеяния и повторного связывания пути». Искусственная эволюция (Ж.-К. Хао, Э.Латтон, Э.Рональд, М.Шоэнауэр, Д.Сньерс, ред.). Лекции по информатике, 1363, Спрингер, Берлин/Гейдельберг, 1998, стр. 13-54.
[3] Диксон, Л. и Г. П. Сегё. «Проблема глобальной оптимизации: введение». К глобальной оптимизации 2 (Диксон, Л.С. В. и Г.П. Сегё, ред.). Амстердам, Нидерланды: Северная Голландия, 1978.