Оптимизация - это процесс нахождения точки, которая минимизирует функцию. Более конкретно:
Локальный минимум функции - это точка, где значение функции меньше или равно значению в соседних точках, но, возможно, больше, чем в удаленной точке.
Глобальный минимум - это точка, в которой значение функции меньше или равно значению во всех других возможных точках.
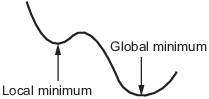
Как правило, решатели Optimization Toolbox™ находят локальный оптимум. (Этот локальный оптимум может быть глобальным оптимумом.) Они находят оптимум в бассейне притяжения отправной точки. Дополнительные сведения см. в разделе Бассейны притяжения.
Напротив, решатели Global Optimization Toolbox предназначены для поиска по нескольким бассейнам притяжения. Они ищут различными способами:
GlobalSearch и MultiStart создать несколько начальных точек. Затем они используют локальный решатель, чтобы найти оптимум в бассейнах притяжения начальных точек.
ga использует набор начальных точек (называемых популяцией) и итеративно генерирует лучшие точки из популяции. Пока первоначальная популяция охватывает несколько бассейнов, ga может осмотреть несколько бассейнов.
particleswarm, например, ga, использует набор начальных точек. particleswarm может исследовать сразу несколько бассейнов из-за их разнообразной популяции.
simulannealbnd выполняет случайный поиск. Как правило, simulannealbnd принимает точку, если она лучше предыдущей. simulannealbnd иногда принимает худшую точку, чтобы достичь другого бассейна.
patternsearch просматривает несколько соседних точек, прежде чем принять одну из них. Если некоторые соседние точки принадлежат разным бассейнам, patternsearch по сути смотрится сразу в ряде бассейнов.
surrogateopt начинается с квазирандомной выборки в пределах границ, ища небольшое значение целевой функции. surrogateopt использует функцию качества, которая, в частности, отдает предпочтение точкам, которые далеки от оцененных точек, что является попыткой достичь глобального решения. После того, как она не может улучшить текущую точку, surrogateopt сбрасывается, заставляя его снова широко пробовать в пределах границ. Сброс - это другой способ surrogateopt ищет глобальное решение.
Если целевая функция f (x) является гладкой, вектор - ∇f (x) указывает в направлении, где f (x) уменьшается наиболее быстро. Уравнение самого крутого спуска, а именно
t)),
вырабатывает путь x (t), который переходит к локальному минимуму, когда t становится большим. Как правило, начальные значения x (0), которые близки друг к другу, дают наиболее крутые пути спуска, которые стремятся к одной и той же минимальной точке. Бассейн притяжения для самого крутого спуска представляет собой набор исходных значений, ведущих к такому же локальному минимуму.
На следующем рисунке показаны два одномерных минимума. На рисунке изображены различные бассейны притяжения с разными стилями линий, а также показаны направления самого крутого спуска со стрелками. Для этой и последующих фигур чёрные точки представляют локальные минимумы. Каждый самый крутой путь спуска, начиная с точки x (0), переходит к черной точке в бассейне, содержащем x (0).
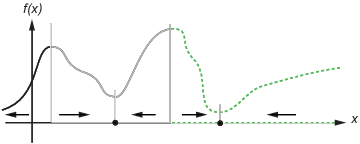
На следующем рисунке показано, как самые крутые пути спуска могут быть сложнее в большем количестве размеров.
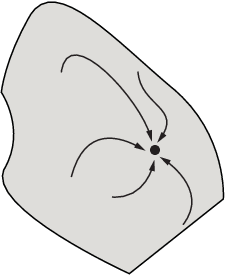
На следующем рисунке показаны еще более сложные пути и бассейны притяжения.

Ограничения могут разбить один бассейн притяжения на несколько частей. Например, рассмотрите возможность минимизации y при следующих условиях:
y ≥ | x |
y ≥ 5 - 4 (x-2) 2.
На рисунке показаны два бассейна притяжения с конечными точками.
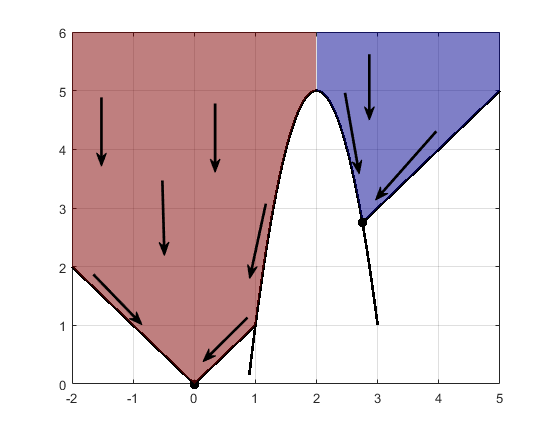
Самые крутые пути спуска - это прямые до границ зависимости. От границ зависимости самые крутые траектории спуска перемещаются вниз вдоль границ. Конечной точкой является либо (0,0), либо (11/4,11/4), в зависимости от того, является ли начальное значение x выше или ниже 2.