Параметры по умолчанию не могут найти глобальный минимум - добавить границы
Мультизапуск без границ, широко распределенные начальные точки
MultiStart с обычной сеткой и перспективными начальными точками
Найти начальную точку в бассейне притяжения глобального минимума может быть трудно, когда бассейн небольшой или когда вы не уверены в местоположении минимума. Для решения этой проблемы можно:
Добавление разумных границ
Возьмите огромное количество случайных начальных точек
Создание методической сетки начальных точек
Для неограниченной задачи возьмите широко рассредоточенные случайные начальные точки
В этом примере показаны эти методы и некоторые варианты.
Функция -sech (x) почти равна 0 для всех | x | > 5, а -sech ( 0) = -1. Примером является двумерная версия функции sech с одним минимальным значением[1,1], другой в [1e5,-1e5]:
f (x, y) = -10sech (| x - (1,1) |) - 20sech (.0003 (| x - (1e5, -1e5) |) - 1.
f имеет глобальный минимум -21 ат (1е5, -1е5) и локальный минимум -11 ат (1,1).
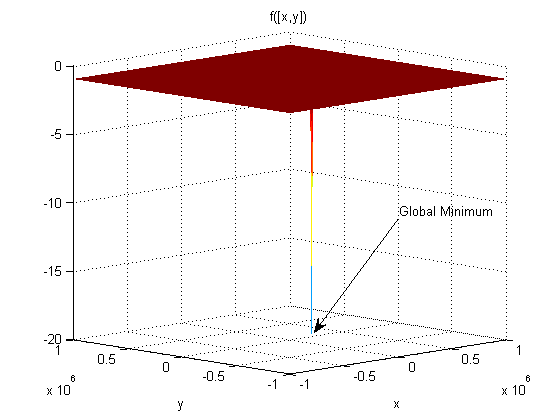
Минимум при (1e5, -1e5) отображается как узкий пик. Минимальное значение (1,1) не отображается, так как оно слишком узкое.
В следующих разделах показаны различные методы поиска глобального минимума. Некоторые методы не являются успешными для этой проблемы. Тем не менее каждый метод может оказаться полезным для решения различных проблем.
GlobalSearch и MultiStart не может найти глобальный минимальный дефолт использования глобальными вариантами, так как компоненты стартовой точки по умолчанию находятся в диапазоне (-9999,10001) для GlobalSearch и (-1000,1000) для MultiStart.
С дополнительными границами -1e6 и 1e6 в problem, GlobalSearch обычно не находит глобального минимума:
x1 = [1;1];x2 = [1e5;-1e5];
f = @(x)-10*sech(norm(x(:)-x1)) -20*sech((norm(x(:)-x2))*3e-4) -1;
opts = optimoptions(@fmincon,'Algorithm','active-set');
problem = createOptimProblem('fmincon','x0',[0,0],'objective',f,...
'lb',[-1e6;-1e6],'ub',[1e6;1e6],'options',opts);
gs = GlobalSearch;
rng(14,'twister') % for reproducibility
[xfinal,fval] = run(gs,problem)
GlobalSearch stopped because it analyzed all the trial points.
All 32 local solver runs converged with a positive
local solver exit flag.
xfinal =
1.0000 1.0000
fval =
-11.0000Чтобы найти глобальный минимум, можно найти больше точек. В этом примере используются 1e5 начальных точек и MaxTime из 300 с:
gs.NumTrialPoints = 1e5; gs.MaxTime = 300; [xg,fvalg] = run(gs,problem) GlobalSearch stopped because maximum time is exceeded. GlobalSearch called the local solver 2186 times before exceeding the clock time limit (MaxTime = 300 seconds). 1943 local solver runs converged with a positive local solver exit flag. xg = 1.0e+04 * 10.0000 -10.0000 fvalg = -21.0000
В этом случае GlobalSearch найден глобальный минимум.
Можно также выполнить поиск с помощью MultiStart со многими начальными точками. В этом примере используются 1e5 начальных точек и MaxTime из 300 с:
ms = MultiStart(gs);
[xm,fvalm] = run(ms,problem,1e5)
MultiStart stopped because maximum time was exceeded.
MultiStart called the local solver 17266 times before exceeding
the clock time limit (MaxTime = 300 seconds).
17266 local solver runs converged with a positive
local solver exit flag.
xm =
1.0000 1.0000
fvalm =
-11.0000В этом случае MultiStart не удалось найти глобальный минимум.
Также можно использовать MultiStart поиск неограниченного региона для поиска глобального минимума. Опять же, вам нужно много стартовых точек, чтобы иметь хорошие шансы найти глобальный минимум.
Первые пять строк кода генерируют 10000 широко рассредоточенных случайных начальных точек, используя метод, описанный в разделе Широко рассредоточенные точки для неограниченных компонентов. newprob является структурой проблемы с использованием fminunc локальный решатель и без границ:
rng(0,'twister') % for reproducibility
u = rand(1e4,1);
u = 1./u;
u = exp(u) - exp(1);
s = rand(1e4,1)*2*pi;
stpts = [u.*cos(s),u.*sin(s)];
startpts = CustomStartPointSet(stpts);
opts = optimoptions(@fminunc,'Algorithm','quasi-newton');
newprob = createOptimProblem('fminunc','x0',[0;0],'objective',f,...
'options',opts);
[xcust,fcust] = run(ms,newprob,startpts)
MultiStart completed the runs from all start points.
All 10000 local solver runs converged with a positive
local solver exit flag.
xcust =
1.0e+05 *
1.0000
-1.0000
fcust =
-21.0000В этом случае MultiStart найден глобальный минимум.
Можно также использовать сетку начальных точек вместо случайных начальных точек. Сведения о построении обычной сетки для большего количества размеров или сетки с небольшими возмущениями см. в разделах Однородная сетка или Возмущенная сетка.
xx = -1e6:1e4:1e6; [xxx,yyy] = meshgrid(xx,xx); z = [xxx(:),yyy(:)]; bigstart = CustomStartPointSet(z); [xgrid,fgrid] = run(ms,newprob,bigstart) MultiStart completed the runs from all start points. All 10000 local solver runs converged with a positive local solver exit flag. xgrid = 1.0e+004 * 10.0000 -10.0000 fgrid = -21.0000
В этом случае MultiStart найден глобальный минимум.
Создание регулярной сетки начальных точек, особенно в больших размерах, может использовать чрезмерное количество памяти или времени. Можно фильтровать начальные точки для выполнения только тех, которые имеют небольшое значение целевой функции.
Чтобы выполнить эту фильтрацию наиболее эффективно, запишите целевую функцию векторизированным образом. Дополнительные сведения см. в разделе Запись векторизованной функции или векторизация целевой функции и функций ограничения. Следующий дескриптор функции вычисляет вектор целей на основе входной матрицы, строки которой представляют начальные точки:
x1 = [1;1];x2 = [1e5;-1e5];
g = @(x) -10*sech(sqrt((x(:,1)-x1(1)).^2 + (x(:,2)-x1(2)).^2)) ...
-20*sech(sqrt((x(:,1)-x2(1)).^2 + (x(:,2)-x2(2)).^2))-1;Предположим, нужно запустить локальный решатель только для точек, где значение меньше -2. Начните с более плотной сетки, чем в MultiStart с обычной сеткой начальных точек, а затем отфильтруйте все точки с высоким значением функции:
xx = -1e6:1e3:1e6;
[xxx,yyy] = meshgrid(xx,xx);
z = [xxx(:),yyy(:)];
idx = g(z) < -2; % index of promising start points
zz = z(idx,:);
smallstartset = CustomStartPointSet(zz);
opts = optimoptions(@fminunc,'Algorithm','quasi-newton','Display','off');
newprobg = createOptimProblem('fminunc','x0',[0,0],...
'objective',g,'options',opts);
% row vector x0 since g expects rows
[xfew,ffew] = run(ms,newprobg,smallstartset)
MultiStart completed the runs from all start points.
All 2 local solver runs converged with a positive
local solver exit flag.
xfew =
100000 -100000
ffew =
-21В этом случае MultiStart найден глобальный минимум. В есть только две начальные точки smallstartset, один из которых является глобальным минимумом.