Уточнение начальных точек

Сведения об уточнении начальных точек

Если некоторые компоненты проблемы не ограничены, GlobalSearch и MultiStart используйте искусственные границы для создания случайных начальных точек равномерно в каждом компоненте. Тем не менее, если ваша проблема имеет далекоидущие минимумы, вам нужны широко рассредоточенные начальные точки, чтобы найти эти минимумы.

Используйте следующие методы для получения широко распределенных начальных точек:

Дайте широко разделенные границы в вашем problem структура.
Использовать RandomStartPointSet объект с MultiStart алгоритм. Установка большого значения ArtificialBound свойство в RandomStartPointSet объект.
Использовать CustomStartPointSet объект с MultiStart алгоритм. Используйте широко распределенные начальные точки.

Каждый способ имеет свои преимущества и недостатки.

Метод	Преимущества	Недостатки
Дать границы в `problem`	Автоматическое формирование точек	Делает более сложный гессен
	Может использоваться с `GlobalSearch`	Неясно, насколько велики границы
	Простота в работе	Изменения `problem`
	Границы могут быть асимметричными	Только однородные точки
Большой `ArtificialBound` в `RandomStartPointSet`	Автоматическое формирование точек	`MultiStart` только
	Не изменяется `problem`	Только симметричные, однородные точки
	Простота в работе	Неясно, какой размер установить `ArtificialBound`
`CustomStartPointSet`	Настраиваемый	`MultiStart` только
`CustomStartPointSet`	Не изменяется `problem`	Требуется программирование для генерации точек

Методы формирования начальных точек

Однородная сетка
Возмущенная сетка
Широко распределенные точки для компонентов без ограничений

Однородная сетка

Чтобы создать однородную сетку начальных точек:

Создание многомерных массивов с помощью ndgrid. Задайте нижнюю границу, интервал и верхнюю границу для каждого компонента.
Например, чтобы создать набор трехмерных массивов с
- Первый компонент от -2 до 0, интервал 0,5
- Вторая составляющая от 0 до 2, шаг 0,25
- Третий компонент от -10 до 5, интервал 1
```
[X,Y,Z] = ndgrid(-2:.5:0,0:.25:2,-10:5);
```
Поместите массивы в одну матрицу, каждая строка которой представляет одну начальную точку. Например:
```
W = [X(:),Y(:),Z(:)];
```
В этом примере: W является матрицей 720 на 3.
Поместите матрицу в CustomStartPointSet объект. Например:
```
custpts = CustomStartPointSet(W);
```

Звонить run с CustomStartPointSet объект в качестве третьего входа. Например,

% Assume problem structure and ms MultiStart object exist
[x,fval,flag,outpt,manymins] = run(ms,problem,custpts);

Возмущенная сетка

Целочисленные начальные точки могут дать менее надежные решения, чем слегка возмущенные начальные точки.

Чтобы получить возмущенный набор начальных точек:

Создайте матрицу начальных точек, как в шагах 1-2 Однородной сетки (Uniform Grid).
Возмутите начальные точки, добавив случайную нормальную матрицу со средним значением 0 и относительно небольшой дисперсией.
Для примера в Uniform Grid после выполнения W матрица, добавьте возмущение:
```
[X,Y,Z] = ndgrid(-2:.5:0,0:.25:2,-10:5);
W = [X(:),Y(:),Z(:)];
W = W + 0.01*randn(size(W));
```
Поместите матрицу в CustomStartPointSet объект. Например:
```
custpts = CustomStartPointSet(W);
```

Звонить run с CustomStartPointSet объект в качестве третьего входа. Например,

% Assume problem structure and ms MultiStart object exist
[x,fval,flag,outpt,manymins] = run(ms,problem,custpts);

Широко распределенные точки для компонентов без ограничений

В некоторых компонентах проблемы могут отсутствовать верхние или нижние границы. Например:

Хотя явных ограничений не существует, существуют уровни, которые компоненты не могут достичь. Например, если один компонент представляет массу одного алмаза, имеется неявная верхняя граница 1 кг (алмаз Хоупа составляет менее 10 г). В таком случае задайте неявную границу в качестве верхней границы.
Действительно нет верхней границы. Например, размер файла компьютера в байтах не имеет эффективной верхней границы. Самый большой размер может быть в гигабайтах или терабайтах сегодня, но через 10 лет, кто знает?

Для действительно неограниченных компонентов можно использовать следующие методы выборки. Чтобы создать приблизительно 1/n точек в каждой области (exp (n), exp (n + 1)), используйте следующую формулу. Если u является случайным и равномерно распределен от 0 до 1, то r = 2u - 1 равномерно распределяется между -1 и 1. Бери

$y = sgn (r) (exp (1/| r$ |) − e).

y симметричен и случайен. Для переменной, ограниченной ниже lbБери

$y = lb + (\exp (1/u$ ) − e).

Аналогично, для переменной, ограниченной выше ubБери

$y = ub - (\exp (1/u$ ) − e).

Например, предположим, что у вас есть трехмерная проблема с

x(1) > 0
x(2) < 100
x(3) без ограничений

Чтобы сделать 150 начальных точек удовлетворяющими этим ограничениям:

u = rand(150,3);
r1 = 1./u(:,1);
r1 = exp(r1) - exp(1);
r2 = 1./u(:,2);
r2 = -exp(r2) + exp(1) + 100;
r3 = 1./(2*u(:,3)-1);
r3 = sign(r3).*(exp(abs(r3)) - exp(1));
custpts = CustomStartPointSet([r1,r2,r3]);

Ниже приведен вариант этого алгоритма. Создайте число от 0 до бесконечности методом для нижних границ. Используйте это число в качестве радиуса точки. Создайте другие компоненты точки, взяв случайные числа для каждого компонента и умножив их на радиус. Можно нормализовать случайные числа перед умножением на радиус, поэтому их норма равна 1. Проработанный пример этого метода см. в разделе MultiStart Without Bounds, Широко распределенные начальные точки.

Пример: Поиск лучшего решения

MultiStart не удается найти глобальный минимум в Multiple Local Minima Via MultiStart. Существует два простых способа поиска лучшего решения:

Использовать дополнительные начальные точки
Задать более жесткие границы на пространстве поиска

Настройка структуры проблемы и MultiStart объект:

problem = createOptimProblem('fminunc',...
    'objective',@(x)sawtoothxy(x(1),x(2)),...
    'x0',[100,-50],'options',...
    optimoptions(@fminunc,'Algorithm','quasi-newton'));
ms = MultiStart;

Использовать дополнительные начальные точки

Управляемый MultiStart по проблеме для 200 начальных точек вместо 50:

rng(14,'twister') % for reproducibility
[x,fval,eflag,output,manymins] = run(ms,problem,200)

MultiStart completed some of the runs from the start points.

53 out of 200 local solver runs converged with a positive local solver exit flag.

x =

   1.0e-06 *

   -0.2284   -0.5567


fval =

   2.1382e-12


eflag =

     2


output = 

  struct with fields:

                funcCount: 32670
         localSolverTotal: 200
       localSolverSuccess: 53
    localSolverIncomplete: 147
    localSolverNoSolution: 0
                  message: 'MultiStart completed some of the runs from the start points.↵↵53 out of 200 local solver runs converged with a positive local solver exit flag.'

manymins = 
  1x53 GlobalOptimSolution

  Properties:
    X
    Fval
    Exitflag
    Output
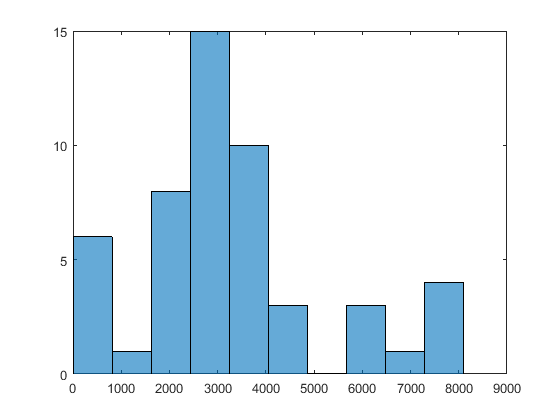
    X0

На этот раз MultiStart нашли глобальный минимум и нашли 51 локальный минимум.

Для просмотра диапазона локальных решений введите histogram([manymins.Fval],10).

Более плотная граница в начальных точках

Предположим, что у интересных локальных решений абсолютные значения всех компонентов меньше 100. Значение по умолчанию границы в начальных точках равно 1000. Чтобы использовать другое значение границы, создайте RandomStartPointSet с ArtificialBound свойство имеет значение 100:

startpts = RandomStartPointSet('ArtificialBound',100,...
    'NumStartPoints',50);
[x,fval,eflag,output,manymins] = run(ms,problem,startpts)

MultiStart completed some of the runs from the start points.

29 out of 50 local solver runs converged with a positive local solver exit flag.

x =

   1.0e-08 *

    0.9725   -0.6198


fval =

   1.4955e-15


eflag =

     2


output = 

  struct with fields:

                funcCount: 7431
         localSolverTotal: 50
       localSolverSuccess: 29
    localSolverIncomplete: 21
    localSolverNoSolution: 0
                  message: 'MultiStart completed some of the runs from the start points.↵↵29 out of 50 local solver runs converged with a positive local solver exit flag.'

manymins = 
  1x25 GlobalOptimSolution

  Properties:
    X
    Fval
    Exitflag
    Output
    X0

MultiStart нашел глобальный минимум и нашел 22 отдельных локальных решения. Для просмотра диапазона локальных решений введите histogram([manymins.Fval],10).

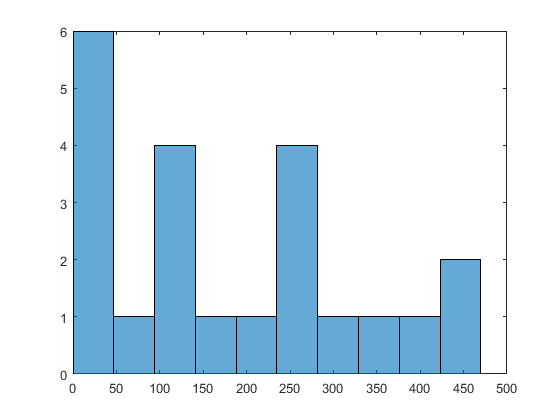
По сравнению с минимумами, найденными в разделе «Использовать больше начальных точек», этот прогон обнаружил лучшие (меньшие) минимумы и имел более высокий процент успешных прогонов.

Документация