В этом примере показано, как найти набор Парето для двухобъектной функции двух переменных. В примере представлены два подхода к минимизации: использование задачи «Оптимизировать интерактивный редактор» и работа в командной строке.
Двухобъектная функция f (x), где x также является двумерной,
x24 + x1x2 − (x1x2) 2.
Создайте новый сценарий в реальном времени, нажав кнопку «Создать сценарий в реальном времени» в разделе «Файл» на вкладке «Главная».
Вставка задачи «Оптимизировать интерактивный редактор». Перейдите на вкладку Вставка, а затем в разделе Код выберите Задача > Оптимизировать.
Для использования при вводе данных о проблемах вставьте новый раздел, нажав кнопку «Разрыв раздела» на вкладке «Вставка». Новые разделы появляются над и под задачей.
В новом разделе над задачей введите следующий код для определения количества переменных и нижней и верхней границ.
nvar = 2; lb = [0 -5]; ub = [5 0];
Чтобы поместить эти переменные в рабочее пространство, запустите раздел, нажав клавиши CTRL + ENTER.
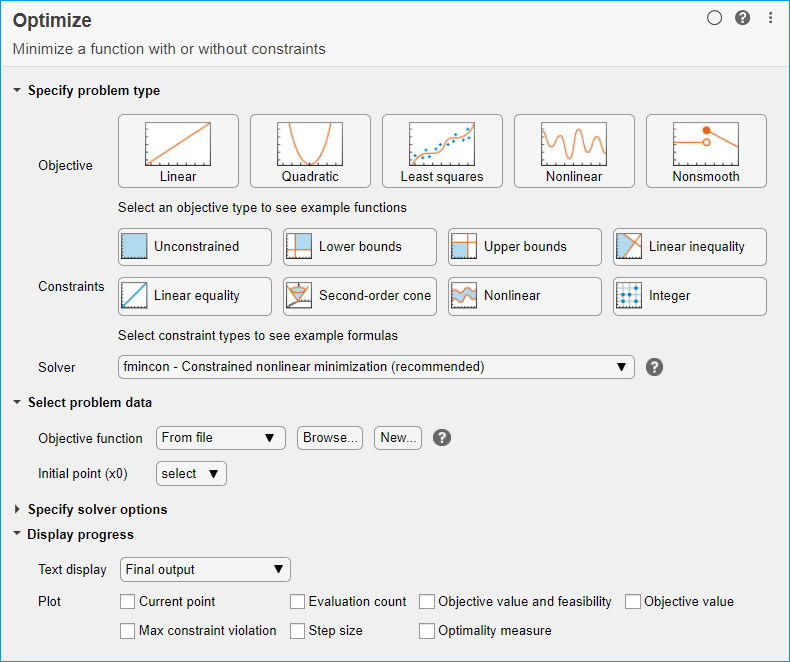
Укажите тип проблемы
В разделе Задание типа задачи нажмите кнопку Цель > Нелинейный.
Нажмите кнопки «Ограничения» > «Нижние границы» и «Верхние границы».
Выберите Решатель > gamultiobj - Многообъективная оптимизация с использованием генетического алгоритма.
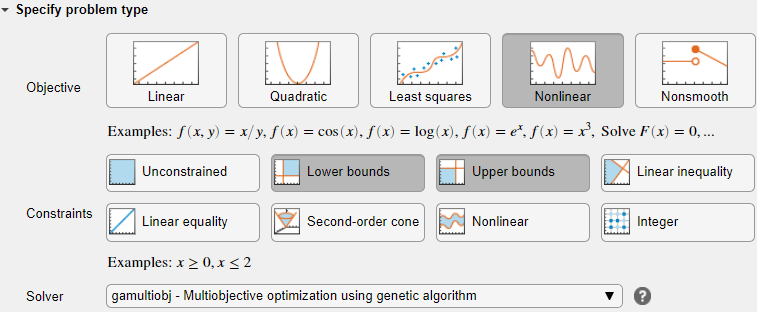
Выбор данных проблемы
В разделе Выбор данных проблемы выберите Целевая функция > Локальная функция, а затем нажмите кнопку Создать. Функция появится в новом разделе под задачей.
Отредактируйте результирующее определение функции, чтобы оно содержало следующий код.
function f = mymulti1(x) f(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - (x(1)*x(2))^2; f(1) = f(2) - 10*x(1)^2; end
В разделе Select problem data выберите функцию Local function > mymulti1.
Выберите Число переменных > nvar.
Выберите Нижние границы > Из рабочей области > Lb и Верхние границы > Из рабочей области > ub.
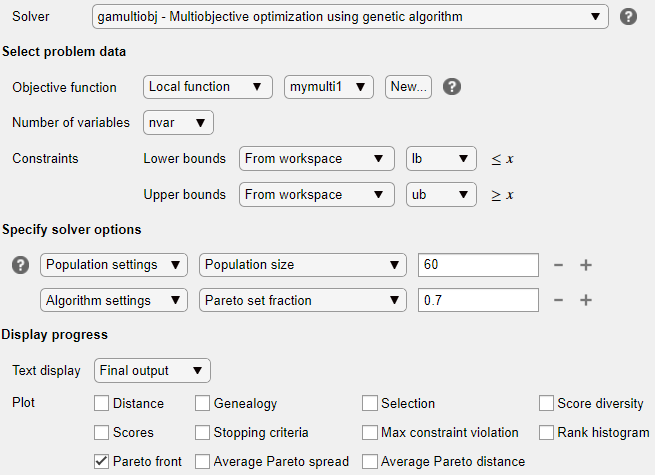
Задать параметры решателя
Разверните раздел Задание параметров решателя и нажмите кнопку Добавить. Чтобы иметь более плотный и подключенный фронт Pareto, укажите больше, чем по умолчанию, выбрав Параметры населения > Размер населения > 60.
Для увеличения числа пользователей на передней панели Pareto по сравнению с настройками по умолчанию нажмите кнопку +. В полученных опциях выберите Алгоритм > Парето задать дробь > 0,7.
Задать параметры отображения
В разделе «Ход выполнения» задачи выберите функцию переднего графика «Парето».
Запустить решатель и проверить результаты
Чтобы запустить решатель, нажмите кнопку опций ⁝ в правом верхнем углу окна задачи и выберите Выполнить раздел. График отображается в отдельном окне рисунка и в области вывода задания.
![Set of points on a convex curve from about [-38,33] to about [-5,0]](multiobj_plot2.png)
График показывает компромисс между двумя компонентами f, который строится в пространстве целевой функции. Для получения более подробной информации см. рис. 9-2, Набор решений Noninferior.
Чтобы выполнить ту же оптимизацию в командной строке, выполните следующие действия.
Создать mymulti1 файл целевой функции по пути MATLAB ®.
function f = mymulti1(x) f(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - (x(1)*x(2))^2; f(1) = f(2) - 10*x(1)^2; end
Задайте параметры и границы.
options = optimoptions('gamultiobj','PopulationSize',60,... 'ParetoFraction',0.7,'PlotFcn',@gaplotpareto); lb = [0 -5]; ub = [5 0];
Выполните оптимизацию с помощью опций.
[solution,ObjectiveValue] = gamultiobj(@mymulti1,2,...
[],[],[],[],lb,ub,options);Задача «Оптимизировать интерактивный редактор» и командная строка позволяют формулировать и решать задачи, и они дают одинаковые результаты. Командная строка является более удобной, но предоставляет меньше возможностей для выбора решателя, настройки проблемы и выбора таких параметров, как функции печати. Можно также запустить проблему с помощью команды Оптимизировать (Optimize), а затем создать код для использования в командной строке, как в разделе Решение ограниченной нелинейной проблемы на основе решателя (Solver-Based).
Эту проблему можно просмотреть другими способами. Следующий рисунок содержит график кривых уровня двух целевых функций, границы Парето, рассчитанные gamultiobj (прямоугольники) и значения x истинного рубежа Парето (алмазы, соединенные почти прямой линией). Истинные граничные точки Парето - это точки, в которых кривые уровня целевых функций параллельны. Алгоритм вычисляет эти точки, обнаруживая, где градиенты целевых функций параллельны. Рисунок печатается в пространстве параметров; см. рис. 9-1, Отображение из пространства параметров в пространство целевой функции.
Контуры объективных функций и границы Парето
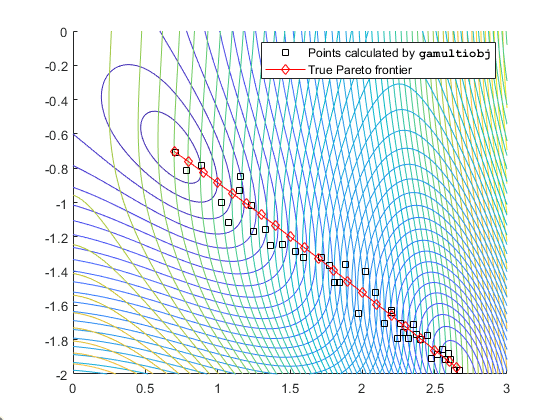
gamultiobj находит концы отрезка линии, то есть находит всю протяженность границы Парето.