Методы непрерывного дискретного преобразования

System Identification Toolbox™ предлагает несколько методов дискретизации и интерполяции для преобразования идентифицированных динамических системных моделей между непрерывным временем и дискретным временем и для повторной дискретизации дискретных временных моделей. Некоторые методы имеют тенденцию обеспечивать лучшее соответствие частотной области между исходной и преобразованной системами, в то время как другие обеспечивают лучшее соответствие во временной области. Используйте следующую таблицу для выбора метода, наиболее подходящего для приложения.

Метод дискретизации	Использовать при
Удержание нулевого заказа	Требуется точная дискретизация во временной области для входов лестницы.
Удержание первого заказа	Требуется точная дискретизация во временной области для кусочно-линейных входов.
Импульсно-инвариантное отображение (только непрерывное-дискретное преобразование)	Требуется точная дискретизация во временной области для входов импульсного поезда.
Аппроксимация Тустина	Требуется хорошее согласование в частотной области между моделями непрерывного и дискретного времени. Ваша модель имеет важную динамику с определенной частотой.
Эквиваленты соответствия нулевого полюса	У вас есть модель SISO. Требуется хорошее согласование в частотной области между моделями непрерывного и дискретного времени.
Наименьшие квадраты (панель инструментов системы управления) (только непрерывное-дискретное преобразование)	У вас есть модель SISO. Требуется хорошее согласование в частотной области между моделями непрерывного и дискретного времени. Вы хотите зафиксировать быструю динамику системы, но должны использовать большее время выборки.

Сведения о том, как задать метод преобразования в командной строке, см. в разделе c2d, d2c, и d2d. В интерактивном режиме можно экспериментировать с различными методами дискретизации в редакторе Live Editor с помощью задачи Преобразовать скорость модели (панель инструментов системы управления) (требуется лицензия).

Удержание нулевого заказа

Метод удержания нулевого порядка (ZOH) обеспечивает точное соответствие между системами непрерывного и дискретного времени во временной области для входов лестницы.

Следующая блок-схема иллюстрирует дискретизацию _Hd (z) с удержанием нулевого порядка линейной модели H (s) непрерывного времени.

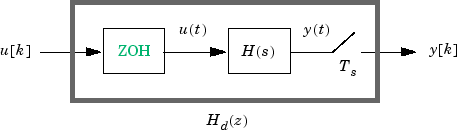
Блок ZOH генерирует входной сигнал u (t) непрерывного времени путем удержания каждого значения u (k) выборки постоянным в течение одного периода выборки:

$u (t) = u [k],_{} kTs≤t≤ (k_{+}$ 1) Ts

Сигнал u (t) является входом в непрерывную систему H (ы). Выходной сигнал y [k] является результатом выборки y (t) _каждые Ts секунд.

И наоборот, учитывая дискретную систему _Hd (z ),d2c создает непрерывную систему H (ы). Дискретизация ZOH H (s) совпадает с Hd ( z).

Дискретное-непрерывное преобразование ZOH имеет следующие ограничения:

d2c не удается преобразовать модели LTI с полюсами при z = 0.
Для дискретно-временных моделей LTI, имеющих отрицательные реальные полюса, ZOH d2c преобразование создает непрерывную систему с более высоким порядком. Порядок модели увеличивается, так как отрицательный вещественный полюс в области z отображается на чисто мнимое значение в области s. Такое отображение приводит к модели непрерывного времени со сложными данными. Чтобы избежать этой проблемы, программное обеспечение вместо этого вводит сопряженную пару комплексных полюсов в области s.

Метод ZOH для систем с временными задержками

Метод ZOH можно использовать для дискретизации моделей непрерывного времени SISO или MIMO с временными задержками. Метод ZOH дает точную дискретизацию для систем с задержками ввода, задержками вывода или задержками передачи.

Для систем с внутренними задержками (задержками в контурах обратной связи) метод ZOH приводит к приблизительным дискретизациям. На следующем рисунке показана система с внутренней задержкой.

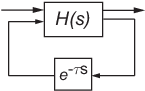
Для таких систем, c2d выполняет следующие действия для вычисления приблизительной дискретизации ZOH:

Анализирует задержку τ как $τ =_{} kTs +ρ$ с $0 ≤ρ <_{Ts}$ .
Поглощает дробную задержку $в$ H (s ).
Дискретизирует H (ы) до H (z).
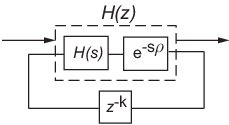
Представляет целую часть задержки _kTs как внутреннюю дискретную временную задержку z-k. Окончательная дискретизированная модель показана на следующем рисунке:

Удержание первого заказа

Метод удержания первого порядка (FOH) обеспечивает точное совпадение между системами непрерывного и дискретного времени во временной области для кусочно-линейных входов.

FOH отличается от ZOH нижележащим механизмом удержания. Чтобы превратить входные выборки u [k] в непрерывный вход u (t), FOH использует линейную интерполяцию между выборками:

$u (t) = u \frac{[k]_{+}}{_{t}} - kTsTs (u [k +_{1}] - u [k]_{)}$ , kTs≤t≤ (k + 1) Ts

В общем, этот метод более точен, чем ZOH для систем, управляемых плавными входами.

Этот метод FOH отличается от стандартного причинного FOH и более уместно называется треугольным приближением (см. [2], стр. 228). Метод также известен как линейно-инвариантная аппроксимация.

Метод FOH для систем с временными задержками

Метод FOH можно использовать для дискретизации моделей непрерывного времени SISO или MIMO с временными задержками. Метод FOH обрабатывает временные задержки так же, как метод ZOH. См. Метод ZOH для систем с временными задержками.

Импульсно-инвариантное отображение

Импульсно-инвариантное отображение создает модель дискретного времени с той же импульсной характеристикой, что и система непрерывного времени. Например, сравните импульсную характеристику непрерывной системы первого порядка с импульсно-инвариантной дискретизацией:

G = tf(1,[1,1]);
Gd1 = c2d(G,0.01,'impulse');
impulse(G,Gd1)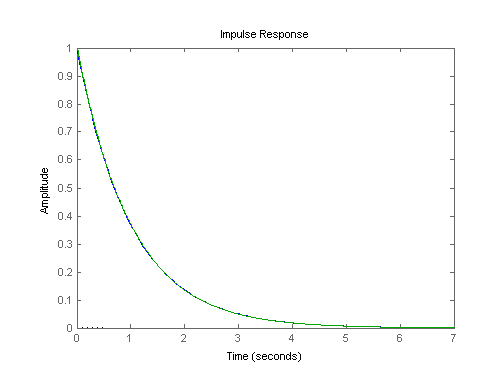

График импульсной характеристики показывает, что импульсные характеристики непрерывных и дискретизированных систем совпадают.

Импульсно-инвариантное отображение для систем с временными задержками

Импульсно-инвариантное отображение можно использовать для дискретизации моделей непрерывного времени SISO или MIMO с задержками времени, за исключением того, что метод не поддерживает ss модели с внутренними задержками. Для поддерживаемых моделей импульсно-инвариантное отображение дает точную дискретизацию временной задержки.

Аппроксимация Тустина

Тустиновое или билинейное приближение дает наилучшее соответствие частотной области между непрерывными и дискретизированными системами. Этот способ связывает передаточные функции s-области и z-области, используя аппроксимацию:

$^{_{}} \frac{_{}}{_{} z=esTs≈1+sTs/21−sTs/2} .$

В c2d при преобразованиях дискретизация _Hd (z) функции непрерывного переноса H (s) составляет:

$_{Hd} (z) =^{H} (s ′)^{,} \frac{}{_{}} \frac{}{}$ s′=2Tsz−1z+1

Аналогично, d2c преобразование опирается на обратное соответствие

$H (s)_{=}^{Hd} (z ′)^{,} \frac{_{}}{_{}}$ z′=1+sTs/21−sTs/2

При преобразовании модели state-space с использованием метода Тустина состояния не сохраняются. Преобразование состояния зависит от матриц «состояние-пространство» и от того, имеет ли система временные задержки. Например, для явной (E = I) модели непрерывного времени без временных задержек вектор состояния w [k] дискретизированной модели связан с вектором состояния непрерывного времени x (t) посредством:

$w [_{} kTs] = (\frac{I_{}}{−} {ATs2}_{)} x \frac{_{(}}{} kTs) -_{} Ts2Bu_{(} \frac{{kTs}_{)}}{} = x (_{} kTs) -_{Ts2} ($ Ax (kTs) + Bu (kTs)).

_Ts - время выборки дискретно-временной модели. A и B - матрицы состояния-пространства модели непрерывного времени.

Аппроксимация Тустина не определена для систем с полюсами при z = -1 и плохо кондиционируется для систем с полюсами около z = -1.

Аппроксимация Tustin с превалированием частоты

Если ваша система имеет важную динамику на определенной частоте, которую вы хотите сохранить преобразование, вы можете использовать метод Tustin с превалированием частоты. Этот метод обеспечивает соответствие между непрерывными и дискретными временными откликами на предвоенной частоте.

Аппроксимация Тустина с превалированием частоты использует следующее преобразование переменных:

$_{Hd} (z) =^{H} (s ′)^{,} \frac{}{{s′=ωtan}_{} (} \frac{ωTs/2}{) z}$ − 1z + 1

Это изменение переменной обеспечивает согласование частотных откликов непрерывного и дискретного времени на предвоенной частоте λ, благодаря следующему соответствию:

$H (jλ)_{=}^{Hd (_{}}$ ejstartTs)

Tustin Approximation для систем с временными задержками

Аппроксимацию Тустина можно использовать для дискретизации моделей непрерывного времени SISO или MIMO с временными задержками.

По умолчанию метод Тастина округляет любую временную задержку до ближайшего кратного времени выборки. Следовательно, для любой временной задержки tau, целая часть задержки, k*Ts, отображает на задержку k периоды выборки в дискретизированной модели. Этот подход игнорирует остаточную дробную задержку, tau - k*Ts.

Можно аппроксимировать дробную часть задержки с помощью дискретного фильтра всех частот (Thiran filter) указанного порядка. Для этого используйте FractDelayApproxOrder вариант c2dOptions.

Чтобы понять, как метод Тастина обрабатывает системы с временными задержками, рассмотрим следующую модель состояния-пространства SISO G (s). Модель имеет входную задержку, выходную задержку, и внутреннюю задержку.

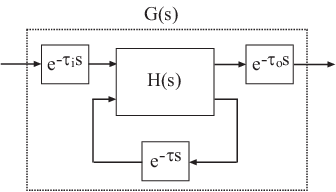
На следующем рисунке показан общий результат дискретизации G (s) с использованием метода Тустина.

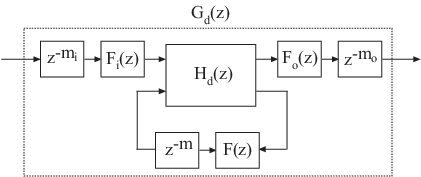
По умолчанию c2d преобразует временные задержки в чистые целочисленные временные задержки. c2d команда вычисляет целочисленные задержки путем округления каждой временной задержки до ближайшего кратного времени выборки _Ts. Таким образом, в случае по умолчанию _mi = скругление (_starti/Ts), _mo =round(_starto/Ts), и m = round(start/Ts).. Также в этом случае _Fi (z) = _Fo (z) = F (z) = 1.

Если установить FractDelayApproxOrder ненулевое значение, c2d аппроксимирует дробную часть временных задержек фильтрами _{Thiran Fi} (z), _Fo (z) и F ( z).

Фильтры Thiran добавляют в модель дополнительные состояния. Максимальное количество дополнительных состояний для каждой задержки: FractDelayApproxOrder.

Например, для входной задержки _starti порядок фильтра Тирэна _Fi (z) равен:

order(_Fi (z)) =max(ceil(_starti/Ts), FractDelayApproxOrder).

Если ceil(_starti/Ts) < FractDelayApproxOrderфильтр Тирэна _Fi (z) аппроксимирует всю входную задержку _starti. Еслиceil(_starti/Ts) > FractDelayApproxOrderфильтр Тирана аппроксимирует только часть входной задержки. В этом случае c2d представляет остаток входной задержки как цепочку единичных задержек ^_z-mi, где

_mi = ceil(_starti/Ts) - FractDelayApproxOrder

c2d использует фильтры Thiran и FractDelayApproxOrder аналогичным образом, чтобы аппроксимировать выходную задержку

При дискретизацииtf и zpk модели по методу Тастина, c2d сначала агрегирует все входные, выходные и транспортные задержки в единую транспортную задержку, для каждого канала. c2d затем аппроксимирует tiTOT как фильтр Тирэна и цепочку единичных задержек таким же образом, как описано для каждой из временных задержек в ss модели.

Дополнительные сведения о фильтрах Thiran см. в разделе thiran( Панель инструментов системы управления) и [4].

Эквиваленты соответствия нулевого полюса

Этот метод преобразования, который вычисляет эквиваленты согласования нулевых полюсов, применяется только к системам SISO. Непрерывные и дискретизированные системы имеют соответствующие коэффициенты усиления постоянного тока. Их полюса и нули связаны преобразованием:

$_{zi} =^{_{}_{}}$ esIts

где:

_zi - i-й полюс или ноль дискретной временной системы.
_si - i-й полюс или ноль системы непрерывного времени.
_Ts - время выборки.

Для получения дополнительной информации см. [2].

Сопоставление нулевого полюса для систем с задержками по времени

Сопоставление нулевых полюсов можно использовать для дискретизации моделей непрерывного времени SISO с задержкой по времени, за исключением того, что метод не поддерживает ss модели с внутренними задержками. Метод сопоставления нулевого полюса обрабатывает временные задержки так же, как и аппроксимацию Тустина. См. Tustin Approximation для систем с временными задержками.

Наименьшие квадраты

Метод наименьших квадратов сводит к минимуму ошибку между частотными откликами систем непрерывного времени и дискретного времени вплоть до частоты Найквиста с использованием подхода оптимизации подбора вектора. Этот метод полезен, когда требуется зафиксировать быструю динамику системы, но необходимо использовать большее время выборки, например, когда вычислительные ресурсы ограничены.

Этот метод поддерживается только c2d функция и только для систем SISO.

Как и при аппроксимации Тустина и согласовании нулевых полюсов, метод наименьших квадратов обеспечивает хорошее соответствие между частотными откликами исходной системы непрерывного времени и преобразованной системы дискретного времени. Однако при использовании метода наименьших квадратов с:

При том же времени выборки, что и при аппроксимации Тустина или согласовании нулевого полюса, получается меньшая разница между частотными откликами непрерывного времени и дискретного времени.
Меньшее время выборки, чем то, что вы бы использовать с Tustin аппроксимации или нулевого полюса сопоставления, вы все еще можете получить результат, который соответствует вашим требованиям. Это полезно, если вычислительные ресурсы ограничены, так как более медленное время выборки означает, что процессор должен выполнять меньше работы.

Ссылки

[1] Острём, К. Дж. и Б. Виттенмарк, компьютерно-управляемые системы: теория и дизайн, Прентис-Холл, 1990, стр. 48-52.

[2] Franklin, G.F., Powell, D.J., and Workman, M.L., Digital Control of Dynamic Systems (3-е издание), Prentice Hall, 1997.

[3] Смит, J.O. III, «Импульсный инвариантный метод», физическая обработка аудиосигналов, август 2007. https://www.dsprelated.com/dspbooks/pasp/Impulse_Invariant_Method.html.

[4] Т. Лааксо, В. Валимаки, «Разделение единичной задержки», IEEE Signal Processing Magazine, Vol. 13, No. 1, p.30-60, 1996.

См. также

Функции

c2d | c2dOptions | d2c | d2cOptions | d2d | d2dOptions | thiran (Панель инструментов системы управления)

Задачи интерактивного редактора

Преобразование скорости модели (панель инструментов системы управления)

Документация