Интерполяция - это метод оценки значения функции в местоположении запроса, которое находится в области набора выборочных точек данных. Значение функции вычисляется на основе выборочных точек данных, ближайших к точке запроса. MATLAB ® может выполнять два вида интерполяции в зависимости от структуры данных выборки. Данные выборки могут образовывать сетку или могут быть разбросаны.
Данные выборки с привязкой к сетке делают интерполяцию более эффективной, поскольку организованная структура данных облегчает MATLAB поиск точек данных выборки, ближайших к точке запроса. Однако интерполяция рассеянных данных требует триангуляции Делоне точек данных, что вводит дополнительный уровень вычисления. Поэтому, если данные можно аппроксимировать как сетку, интерполяция с привязкой к сетке обеспечивает существенную экономию времени вычислений и использования памяти по сравнению с интерполяцией с разбросанными координатами.
Два подхода к интерполяции охватываются следующими темами:
Интерполяция данных с сеткой охватывает интерполяцию 1-D и N-D-интерполяцию данных выборки в формате сетки, выровненном по оси:
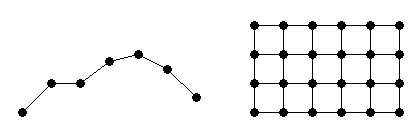
Интерполяция рассеянных данных охватывает N-D интерполяцию рассеянных данных:

Методы интерполяции, доступные в MATLAB, создают интерполяционные функции, которые проходят через точки данных выборки. То есть при запросе функции интерполяции в месте выборки возвращается точное значение данных выборки, а не аппроксимация. Напротив, алгоритмы подгонки кривых и поверхностей не обязательно проходят через точки данных выборки. Дополнительные сведения о фитинге кривой см. в разделе Панель инструментов фитинга кривой.
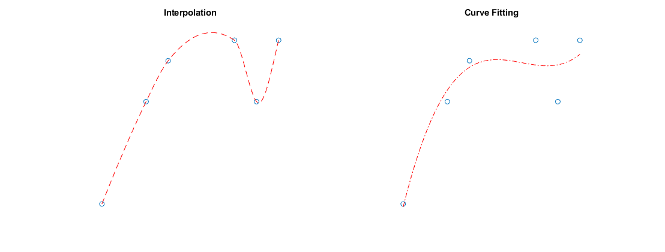
В некоторых случаях может потребоваться аппроксимация сетки для данных. Например, сетка может иметь точки, лежащие вдоль кривых линий. Такой набор данных может возникнуть, если данные основаны на долготе и широте:
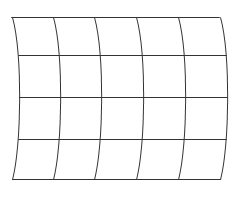
С криволинейной сеткой вы эффективно работаете с набором рассеянных данных и должны использовать для интерполяции значений более дорогостоящие в вычислительном отношении функции рассеянной интерполяции. Однако, хотя входные данные не могут быть привязаны непосредственно к сетке, иногда возможно аппроксимировать криволинейную сетку прямыми линиями сетки через соответствующие интервалы:
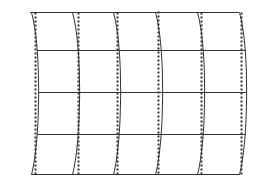
Можно создать аппроксимированную сетку, создав набор векторов сетки с соответствующим интервалом. Аппроксимация кривой сетки прямыми линиями позволяет получить преимущества производительности интерполяции на основе сетки, ценой небольшого искажения данных. Дополнительные сведения о создании векторов сетки см. в разделе Представления сетки.
griddedInterpolant | scatteredInterpolant