Сетчатые данные состоят из значений или измерений в регулярно разнесенных точках, которые образуют сетку. Сетчатые данные возникают во многих областях, таких как метеорология, съемка и медицинская визуализация. В этих областях обычно проводят измерения через регулярные пространственные интервалы, возможно, с течением времени. Эти упорядоченные сетки данных могут варьироваться от 1-D (для простых временных рядов) до 4-D (для измерения объемов во времени) или выше. Некоторые примеры данных с привязкой к сетке:
1-D: Цены акций со временем
2-D: Температура поверхности
3-D: МРТ-изображение мозга
4-D: Измерения океана в объеме воды с течением времени
Во всех этих приложениях интерполяция на основе сетки эффективно расширяет полезность данных до точек, где измерения не проводились. Например, при наличии данных почасовой цены для запаса можно использовать интерполяцию для аппроксимации цены каждые 15 минут.
MATLAB ® предоставляет несколько инструментов для интерполяции на основе сетки:
meshgrid и ndgrid функции создают сетки различной размерности. meshgrid может создавать 2-D или 3-D сетки, в то время как ndgrid может создавать сетки с любым количеством размеров. Эти функции возвращают сетки с использованием различных форматов вывода. Между этими форматами сетки можно выполнить преобразование с помощью pagetranspose (по состоянию на R2020b год) или permute функции для замены первых двух размеров сетки.
interp семейство функций включает interp1, interp2, interp3, и interpn. Каждая функция предназначена для интерполяции данных с определенным числом измерений. interp2 и interp3 использовать сетки в meshgrid формат, пока interpn использует сетки в ndgrid формат.
griddedInterpolant объекты поддерживают интерполяцию в любом количестве измерений для данных в ndgrid формат. Эти объекты также поддерживают многозначную интерполяцию (начиная с версии R2021a), где каждая точка сетки может иметь несколько связанных с ней значений.
Преимущества использования памяти и производительности griddedInterpolant объекты над interp функции. griddedInterpolant предлагает существенные улучшения производительности для повторных запросов интерполяционного объекта, тогда как interp при каждом вызове функции выполняют новый расчет. Также, griddedInterpolant хранит точки выборки в формате с эффективным использованием памяти (в виде компактной сетки) и многопоточно использует преимущества многоядерных компьютерных процессоров.
MATLAB позволяет представлять сетку в одном из трех представлений: полной сетке, компактной сетке или сетке по умолчанию. Сетка по умолчанию и компактная сетка используются в первую очередь для удобства и повышения эффективности, соответственно.
Полная сетка - это сетка, в которой явно определены все точки. Выходные данные ndgrid и meshgrid определите полную сетку. Можно создать однородные полные сетки, в которых точки в каждом размере имеют одинаковый интервал, или неоднородные, в которых интервал изменяется в одном или нескольких размерах. Однородные сетки могут иметь различные интервалы в каждом размере, если интервал постоянен в пределах каждого размера.
| Униформа | Униформа | Неоднородный |
|---|---|---|
|
|
|
Пример однородной полной сетки:
[X,Y] = meshgrid([1 2 3],[3 6 9 12])
X =
1 2 3
1 2 3
1 2 3
1 2 3
Y =
3 3 3
6 6 6
9 9 9
12 12 12При явном определении каждой точки в сетке может потребляться много памяти при работе с большими сетками. Компактное представление сетки - это способ обойтись без накладных расходов на память полной сетки. В компактном представлении сетки вместо полной сетки хранятся только векторы сетки (по одному для каждого размера). Вместе векторы сетки неявно определяют сетку. Фактически, входные данные для meshgrid и ndgrid являются векторами сетки, и эти функции воспроизводят векторы сетки, чтобы сформировать полную сетку. Компактное представление сетки позволяет обходить создание сетки и подавать векторы сетки непосредственно в функцию интерполяции.
Например, рассмотрим два вектора, x1 = 1:3 и x2 = 1:5. Эти векторы можно рассматривать как набор координат в x1 направление и набор координат в x2 направление, например:
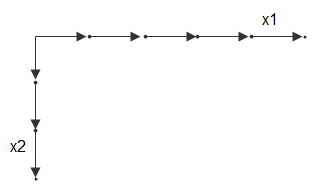
Каждая стрелка указывает на местоположение. Эти два вектора можно использовать для определения набора точек сетки, где один набор координат задается x1 и другой набор координат задается x2. При репликации векторов сетки они образуют два массива координат, составляющих полную сетку:
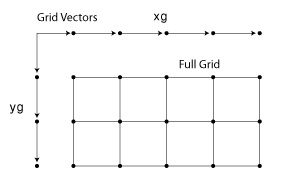
Векторы входных сеток могут быть монотонными или немонотонными. Монотонные векторы содержат значения, которые либо увеличиваются в этом измерении, либо уменьшаются в этом измерении. И наоборот, немонотонные векторы содержат значения, которые колеблются. Если входной вектор сетки не является монотонным, например [2 4 6 3 1], то [X1,X2] = ndgrid([2 4 6 3 1]) выводит немонотонную сетку. Векторы сетки должны быть монотонными, если предполагается передать сетку другим функциям MATLAB. sort функция полезна для обеспечения монотонности.
В некоторых приложениях важны только значения в точках сетки, а не расстояния между точками сетки. Например, большинство МРТ-сканирования собирают данные, которые равномерно разнесены во всех направлениях. В подобных случаях можно разрешить функции интерполяции автоматически создавать представление сетки по умолчанию для использования с данными. Для этого следует исключить входные данные сетки для функции интерполяции. При исключении входных данных сетки функция автоматически учитывает, что данные находятся на сетке с единицами измерения. Функция создает сетку с единицами измерения во время ее выполнения, избавляя вас от проблем с созданием сетки самостоятельно.
Рассмотрим данные о температуре, собранные на поверхности с регулярными интервалами 5 см, простирающимися на 20 см в каждом направлении. Использовать meshgrid для создания полной сетки.
[X,Y] = meshgrid(0:5:20)
X =
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
Y =
0 0 0 0 0
5 5 5 5 5
10 10 10 10 10
15 15 15 15 15
20 20 20 20 20Координаты (x, y) каждой точки сетки представлены в виде соответствующих элементов в X и Y матрицы. Первая точка сетки задается [X(1) Y(1)], что является [0 0], следующая точка сетки задается [X(2) Y(2)], что является [0 5]и так далее.
Теперь создайте матрицу для представления измерений температуры на сетке, а затем постройте график данных в виде поверхности.
T = [1 1 10 1 1;
1 10 10 10 10;
100 100 1000 100 100;
10 10 10 10 1;
1 1 10 1 1];
surf(X,Y,T)
view(2)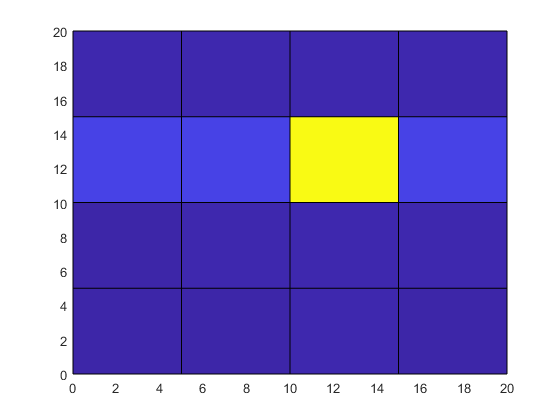
Хотя температура в центральной точке сетки велика, ее местоположение и влияние на окружающие точки сетки не видны из необработанных данных.
Чтобы улучшить разрешение данных в 10 раз, используйте interp2 для интерполяции данных о температуре на более тонкую сетку, использующую интервалы 0,5 см. Использовать meshgrid для создания более тонкой сетки, представленной матрицами Xq и Yq. Затем используйте interp2 с исходной сеткой, температурными данными и новыми точками сетки и постройте график полученных данных. По умолчанию interp2 использует линейную интерполяцию в каждом измерении.
[Xq,Yq] = meshgrid(0:0.5:20); Tq = interp2(X,Y,T,Xq,Yq); surf(Xq,Yq,Tq) view(2)
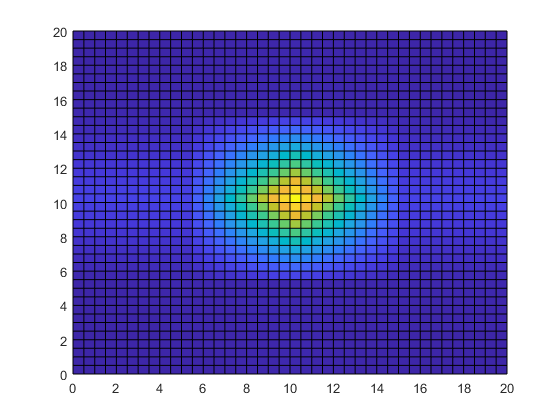
Интерполяция данных о температуре добавляет детали изображению и значительно улучшает полезность данных в области измерений.
Функции и объекты интерполяции на основе сетки в MATLAB предлагают несколько различных методов интерполяции. При выборе метода интерполяции следует помнить, что некоторым требуется больше памяти или больше времени вычислений, чем другим. Возможно, потребуется обменять эти ресурсы для достижения желаемой плавности в результате. В следующей таблице представлен предварительный просмотр каждого метода интерполяции, применяемого к тем же данным 1-D, а также обзор преимуществ, компромиссов и требований для каждого метода.
| Метод | Описание |
|---|---|
|
| Интерполированное значение в точке запроса - это значение в ближайшей выборочной точке сетки.
|
|
| Интерполированное значение в точке запроса - это значение в следующей выборочной точке сетки.
|
|
| Интерполированное значение в точке запроса - это значение в предыдущей выборочной точке сетки.
|
|
| Интерполированное значение в точке запроса основано на линейной интерполяции значений в соседних точках сетки в каждом соответствующем измерении.
|
|
| Интерполированное значение в точке запроса основано на сохраняющей форму частичной кубической интерполяции значений в соседних точках сетки.
|
|
| Интерполированное значение в точке запроса основано на кубической интерполяции значений в соседних точках сетки в каждом соответствующем измерении.
|
|
| Интерполированное значение в точке запроса основано на кусочной функции многочленов со степенью не более трех, вычисленной с использованием значений соседних точек сетки в каждом соответствующем измерении. Формула Акимы модифицируется, чтобы избежать переполнения.
|
|
| Интерполированное значение в точке запроса основано на кубической интерполяции значений в соседних точках сетки в каждом соответствующем измерении.
|
griddedInterpolant | interp1 | interp2 | interp3 | interpn