Сингулярные значения

Сингулярное значение и соответствующие сингулярные векторы прямоугольной матрицы А представляют собой, соответственно, скалярное λ и пару векторов u и v, удовлетворяющих

$\begin{array}{l} Av = \\ ^{} \end{array}$

где $^{AH}$ - эрмитово транспонирование A. Сингулярные векторы u и v обычно масштабируются так, чтобы иметь норму 1. Также, если u и v являются сингулярными векторами A, то -u и -v являются сингулярными векторами A также.

Сингулярные значения λ всегда вещественны и неотрицательны, даже если А сложна. При сингулярных значениях в диагональной матрице Λ и соответствующих сингулярных векторах, образующих столбцы двух ортогональных матриц U и V, получаются уравнения

$\begin{array}{l} AV = \\ ^{} USTARTAHU = \end{array}$ VΛ.

Поскольку U и V - унитарные матрицы, умножение первого уравнения $^{}$ на VH справа даёт уравнение разложения сингулярного значения

$A =^{}$ USTARTVH.

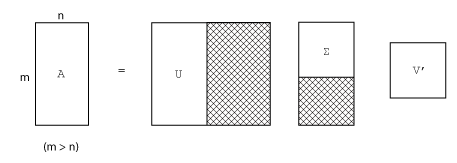
Полное сингулярное разложение матрицы m-на-n включает в себя:

Матрица m-на-m U
матрица m-by-n (m-на-n)
Матрица n-на-n V

Другими словами, U и V оба являются квадратными, а Λ - того же размера, что и A. Если A имеет гораздо больше строк, чем столбцов (m > n), затем полученный результат mоколо-m матрица U большая. Однако большинство столбцов в U умножаются на нули в Λ. В этой ситуации разложение по экономичному размеру экономит как время, так и время хранения за счет получения m-на-n U, n-на-n Λ и того же V:

In the economy-sized decomposition, columns in U can be ignored if they multiply zeros in the diagonal matrix of singular values.

Разложение собственных значений является подходящим инструментом для анализа матрицы, когда она представляет отображение из векторного пространства в себя, как это делается для обычного дифференциального уравнения. Однако разложение сингулярных значений является подходящим инструментом для анализа отображения из одного векторного пространства в другое векторное пространство, возможно, с другой размерностью. Большинство систем одновременных линейных уравнений относятся ко второй категории.

Если A является квадратным, симметричным и положительным определенным, то его собственное значение и сингулярное разложение являются одинаковыми. Но по мере того, как А отходит от симметрии и положительной определённости, разница между двумя разложениями увеличивается. В частности, разложение сингулярного значения вещественной матрицы всегда является действительным, но разложение собственного значения вещественной несимметричной матрицы может быть сложным.

Для примера матрицы

полное разложение сингулярного значения

[U,S,V] = svd(A)

U =

    0.6105   -0.7174    0.3355
    0.6646    0.2336   -0.7098
    0.4308    0.6563    0.6194


S =

   14.9359         0
         0    5.1883
         0         0


V =

    0.6925   -0.7214
    0.7214    0.6925

Вы можете проверить, что U*S*V' равно A в пределах ошибки округления. Для этой небольшой проблемы разложение по размеру экономики лишь немного меньше.

[U,S,V] = svd(A,0)

U =

    0.6105   -0.7174
    0.6646    0.2336
    0.4308    0.6563


S =

   14.9359         0
         0    5.1883


V =

    0.6925   -0.7214
    0.7214    0.6925

Опять же, U*S*V' равно A в пределах ошибки округления.

Аппроксимации SVD низкого ранга

Для больших разреженных матриц используйте svd вычислять все сингулярные значения и сингулярные векторы не всегда целесообразно. Например, если нужно знать только несколько самых больших значений сингулярного числа, то вычисление всех значений сингулярного числа разреженной матрицы 5000 на 5000 является дополнительной работой.

В случаях, когда требуется только подмножество сингулярных значений и сингулярных векторов, svds и svdsketch функции предпочтительнее, чем svd.

Функция Использование

svds Использовать svds для вычисления аппроксимации ранга-k SVD. Можно указать, должно ли подмножество сингулярных значений быть наибольшим, наименьшим или ближайшим к определенному числу. svds обычно вычисляет наилучшее возможное приближение ранга-k.

svdsketch Использовать svdsketch для вычисления частичного SVD входной матрицы, удовлетворяющей заданному допуску. В то время как svds требует указания ранга, svdsketch адаптивно определяет ранг эскиза матрицы на основе заданного допуска. Приближение ранга-k, что svdsketch в конечном итоге использует удовлетворяет допуску, но в отличие от svds, он не гарантированно будет лучшим из возможных.

Функция	Использование
`svds`	Использовать `svds` для вычисления аппроксимации ранга-k SVD. Можно указать, должно ли подмножество сингулярных значений быть наибольшим, наименьшим или ближайшим к определенному числу. `svds` обычно вычисляет наилучшее возможное приближение ранга-k.
`svdsketch`	Использовать `svdsketch` для вычисления частичного SVD входной матрицы, удовлетворяющей заданному допуску. В то время как `svds` требует указания ранга, `svdsketch` адаптивно определяет ранг эскиза матрицы на основе заданного допуска. Приближение ранга-k, что `svdsketch` в конечном итоге использует удовлетворяет допуску, но в отличие от `svds`, он не гарантированно будет лучшим из возможных.

Например, рассмотрим случайную разреженную матрицу 1000 на 1000 с плотностью около 30%.

n = 1000;
A = sprand(n,n,0.3);

Шесть самых больших значений в единственном числе:

S = svds(A)

S =

  130.2184
   16.4358
   16.4119
   16.3688
   16.3242
   16.2838

Кроме того, шестью наименьшими сингулярными значениями являются

S = svds(A,6,'smallest')

S =

    0.0740
    0.0574
    0.0388
    0.0282
    0.0131
    0.0066

Для меньших матриц, которые могут поместиться в память как полная матрица, full(A), использование svd(full(A)) может быть все еще быстрее, чем svds или svdsketch. Однако для действительно больших и разреженных матриц, используя svds или svdsketch становится необходимым.

См. также

gsvd | svd | svds | svdsketch

Документация