(Не рекомендуется) Простой в использовании плоттер 3-D цветной поверхностью
ezsurf не рекомендуется. Использовать fsurf вместо этого.
ezsurf(fun)
ezsurf(fun,domain)
ezsurf(funx,funy,funz)
ezsurf(funx,funy,funz,[smin,smax,tmin,tmax])
ezsurf(funx,funy,funz,[min,max])
ezsurf(...,n)
ezsurf(...,'circ')
ezsurf(axes_handle,...)
h = ezsurf(...)
ezsurf(fun) создает график fun(x,y) с использованием surf функция. fun нанесено на график над областью по умолчанию: -2δ < x < 2π, -2π < y < 2π.
fun может быть дескриптором функции, символьным вектором или строкой (см. раздел Советы).
ezsurf(fun,domain) сюжеты fun поверх указанного domain. domain должен быть вектором. Подробные сведения о векторных входах и предельных выходах осей см. в разделе Алгоритмы.
ezsurf(funx,funy,funz) отображает параметрическую поверхность funx(s,t), funy(s,t), и funz(s,t) над квадратом: -2δ < s < 2π, -2π < t < 2π.
ezsurf(funx,funy,funz,[smin,smax,tmin,tmax]) или ezsurf(funx,funy,funz,[min,max]) отображает параметрическую поверхность с использованием указанной области.
ezsurf(...,n) сюжеты fun над доменом по умолчанию с использованием nоколо-n сетка. Значение по умолчанию для n составляет 60.
ezsurf(...,'circ') сюжеты fun на диске с центром в домене.
ezsurf(axes_handle,...) строит графики в осях с ручкой axes_handle вместо текущих осей (gca).
h = ezsurf(...) возвращает маркер перемещения к объекту поверхности в h.
Постройте график функции x + iy)) над -2pi < и - 2pi < y < 2pi. ezsurf функция не отображает точки, в которых математическая функция не определена. Для этих точек установлено значение NaN чтобы они не заговаривали.
figure
ezsurf('real(atan(x+i*y))')
Использовать surf для печати одних и тех же данных без фильтрации разрывов.
figure [x,y] = meshgrid(linspace(-2*pi,2*pi,60)); z = real(atan(x+1i.*y)); surf(x,y,z)
ezsurf и ezsurfc не принимать сложные входные данные.
Умножение массива, деление и возведение в степень всегда подразумеваются в выражении, которому передается ezsurf. Например, синтаксис MATLAB ® для графика поверхности выражения
sqrt(x.^2 + y.^2);
записывается как
ezsurf('sqrt(x^2 + y^2)')То есть x^2 интерпретируется как x.^2 в векторе символов или строке, в которую вы передаете ezsurf.
Если функция, подлежащая построению, является функцией переменных u и v (а не x и y), то конечные точки домена umin, umax, vmin, и vmax сортируются по алфавиту. Таким образом, ezsurf('u^2 - v^3',[0,1],[3,6]) графики u2 - v3 свыше 0 < u < 1, 3 < v < 6.
Аргументы дескриптора функции должны указывать на функции, использующие синтаксис MATLAB. Например, следующие инструкции определяют анонимную функцию и передают дескриптор функции fh кому ezsurf.
fh = @(x,y) sqrt(x.^2 + y.^2); ezsurf(fh)
Обратите внимание, что при использовании дескрипторов функций необходимо использовать операторы мощности массива, умножения массива и деления массива (.^, .*, ./) с ezsurf не изменяет синтаксис, как в случае с символьными векторными или строковыми входами.
Если функция имеет дополнительные параметры, например, k в myfun:
function z = myfun(x,y,k1,k2,k3) z = x.*(y.^k1)./(x.^k2 + y.^k3);
затем можно использовать анонимную функцию для указания этого параметра:
ezsurf(@(x,y)myfun(x,y,2,2,4))
ezsurf определяет пределы осей X и Y различными способами в зависимости от способа ввода области (если это вообще возможно). В следующей таблице: R является вектором [xmin, xmax, ymin, ymax] и v - вектор домена, введенный вручную.
| Указано число значений домена: | Результирующий вектор домена: |
|---|---|
v = [ ]; |
R = [-2*pi, 2*pi, -2*pi, 2*pi]; |
v = [ v(1) ]; |
R = double([-abs(v),abs(v),-abs(v),abs(v)]); |
v = [ v(1) v(2) ]; |
R = double([v(1),v(2),v(1),v(2)]); |
v = [ v(1) v(2) v(3) ]; |
R = double([-v(1),v(2),-abs(v(3)),abs(v(3))]); |
v = [ v(1) v(2) v(3) v(4) ]; |
R = double(v); |
v = [ v(1)..v(n) ]; n>4 |
R = double([-abs(v(1)), abs(v(1)), -abs(v(1)), abs(v(1))]); |
Если указать одно число в многовекторном формате (без квадратных скобок, []), ezsurf интерпретирует его как n, количество точек между осями max и min значения.
По умолчанию ezsurf использует 60 точек между max и min значения осей. Когда min и max значения являются значениями по умолчанию (R = [-2*pi, 2*pi, -2*pi, 2*pi];), ezsurf обеспечивает попадание 60 точек в несложный диапазон заданного уравнения. Например, − y2 является действительным только x2−y2≤1. График по умолчанию для этой функции выглядит следующим образом:
ezsurf('sqrt(1-x^2-y^2)')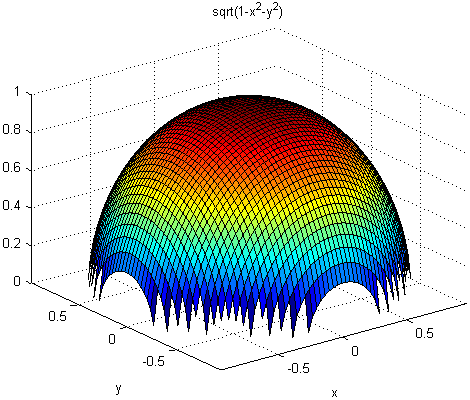
Видно, что между минимальным и максимальным значениями есть 60 точки, для которых − y2has вещественные значения. Однако при указании значений домена, совпадающих со значениями по умолчанию (R = [-2*pi, 2*pi, -2*pi, 2*pi];), появляется другой результат:
ezsurf('sqrt(1-x^2-y^2)',[-2*pi 2*pi])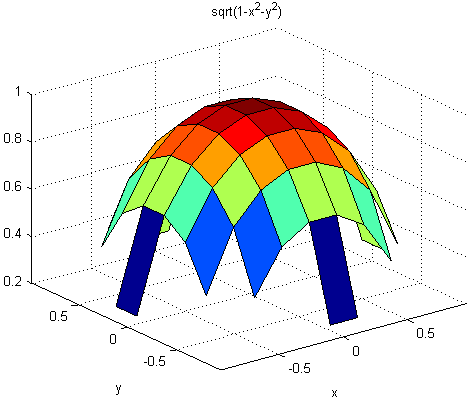
В этом случае графические пределы одинаковы, но ezsurf использовали 60 точек между определяемыми пользователем пределами вместо проверки того, будут ли все эти точки иметь реальные ответы.