1-D интерполяция данных (поиск в таблице)
vq = interp1(x,v,xq)x содержит точки образца, и v содержит соответствующие значения v (x). Векторxq содержит координаты точек запроса.
Если у вас есть несколько наборов данных, которые отбираются в одной точке координаты, то вы можете пройти v в виде массива. Каждый столбец массива v содержит другой набор 1-D значений образцов.
vq = interp1(x,v,xq,method,extrapolation)x. Набор extrapolation кому 'extrap' когда вы хотите использовать method алгоритм экстраполяции. Кроме того, можно указать скалярное значение, в этом случае: interp1 возвращает это значение для всех точек за пределами области x.
vq = interp1(v,xq)1 кому n, где n зависит от формы v:
Если v является вектором, по умолчанию используются следующие точки: 1:length(v).
Если v - массив, точки по умолчанию: 1:size(v,1).
Используйте этот синтаксис, когда вас не волнуют абсолютные расстояния между точками.
vq = interp1(v,xq,method,extrapolation)
pp = interp1(x,v,method,'pp')method алгоритм.
Примечание
Этот синтаксис не рекомендуется. Использовать griddedInterpolant вместо этого.
Определите точки образца, xи соответствующие выборочные значения, v.
x = 0:pi/4:2*pi; v = sin(x);
Определите точки запроса для более точной выборки в диапазоне x.
xq = 0:pi/16:2*pi;
Выполните интерполяцию функции в точках запроса и постройте график результата.
figure vq1 = interp1(x,v,xq); plot(x,v,'o',xq,vq1,':.'); xlim([0 2*pi]); title('(Default) Linear Interpolation');

Теперь оцените v в тех же точках, используя 'spline' способ.
figure vq2 = interp1(x,v,xq,'spline'); plot(x,v,'o',xq,vq2,':.'); xlim([0 2*pi]); title('Spline Interpolation');

Определите набор значений функций.
v = [0 1.41 2 1.41 0 -1.41 -2 -1.41 0];
Определите набор точек запроса, которые попадают между точками по умолчанию. 1:9. В этом случае точками по умолчанию являются 1:9 потому что v содержит 9 значения.
xq = 1.5:8.5;
Оценить v в xq.
vq = interp1(v,xq);
Постройте график результата.
figure plot((1:9),v,'o',xq,vq,'*'); legend('v','vq');

Определите набор точек образца.
x = 1:10;
Определите значения функции v + x2i в точках выборки.
v = (5*x)+(x.^2*1i);
Определите точки запроса для более точной выборки в диапазоне x.
xq = 1:0.25:10;
Интерполировать v в точках запроса.
vq = interp1(x,v,xq);
Постройте график реальной части результата красным цветом, а воображаемой - синим.
figure plot(x,real(v),'*r',xq,real(vq),'-r'); hold on plot(x,imag(v),'*b',xq,imag(vq),'-b');

Интерполяция точек данных с временной меткой.
Рассмотрим набор данных, содержащий показания температуры, которые измеряются каждые четыре часа. Создайте таблицу с данными за один день и постройте график данных.
x = (datetime(2016,1,1):hours(4):datetime(2016,1,2))'; x.Format = 'MMM dd, HH:mm'; T = [31 25 24 41 43 33 31]'; WeatherData = table(x,T,'VariableNames',{'Time','Temperature'})
WeatherData=7×2 table
Time Temperature
_____________ ___________
Jan 01, 00:00 31
Jan 01, 04:00 25
Jan 01, 08:00 24
Jan 01, 12:00 41
Jan 01, 16:00 43
Jan 01, 20:00 33
Jan 02, 00:00 31
plot(WeatherData.Time, WeatherData.Temperature, 'o')
Интерполяция набора данных для прогнозирования показаний температуры в течение каждой минуты дня. Поскольку данные являются периодическими, используйте 'spline' способ интерполяции.
xq = (datetime(2016,1,1):minutes(1):datetime(2016,1,2))';
V = interp1(WeatherData.Time, WeatherData.Temperature, xq, 'spline');Постройте график интерполированных точек.
hold on plot(xq,V,'r')

Определите точки образца, xи соответствующие выборочные значения, v.
x = [1 2 3 4 5]; v = [12 16 31 10 6];
Укажите точки запроса, xq, которые выходят за пределы области x.
xq = [0 0.5 1.5 5.5 6];
Оценить v в xq с использованием 'pchip' способ.
vq1 = interp1(x,v,xq,'pchip')vq1 = 1×5
19.3684 13.6316 13.2105 7.4800 12.5600
Далее оцените v в xq с использованием 'linear' способ.
vq2 = interp1(x,v,xq,'linear')vq2 = 1×5
NaN NaN 14 NaN NaN
Теперь используйте 'linear' с помощью 'extrap' вариант.
vq3 = interp1(x,v,xq,'linear','extrap')
vq3 = 1×5
8 10 14 4 2
'pchip' экстраполяция по умолчанию, но 'linear' не делает.
Определите точки образца, xи соответствующие выборочные значения, v.
x = [-3 -2 -1 0 1 2 3]; v = 3*x.^2;
Укажите точки запроса, xq, которые выходят за пределы области x.
xq = [-4 -2.5 -0.5 0.5 2.5 4];
Теперь оцените v в xq с использованием 'pchip' метод и назначить любые значения за пределами области x к значению, 27.
vq = interp1(x,v,xq,'pchip',27)vq = 1×6
27.0000 18.6562 0.9375 0.9375 18.6562 27.0000
Определите точки образца.
x = (-5:5)';
Пример трех различных параболических функций в точках, определенных в x.
v1 = x.^2; v2 = 2*x.^2 + 2; v3 = 3*x.^2 + 4;
Создать матрицу v, столбцы которых являются векторами, v1, v2, и v3.
v = [v1 v2 v3];
Определение набора точек запроса, xq, чтобы быть более тонкой выборкой в диапазоне x.
xq = -5:0.1:5;
Оценить все три функции в xq и постройте график результатов.
vq = interp1(x,v,xq,'pchip'); figure plot(x,v,'o',xq,vq); h = gca; h.XTick = -5:5;

Круги на графике представляют v, и сплошные линии представляют vq.
x - Выборочные точкиВыборочные точки, определяемые как вектор строки или столбца вещественных чисел. Значения в x должны быть различными. Длина x должны соответствовать одному из следующих требований:
Если v является вектором, то length(x) должны равняться length(v).
Если v является массивом, то length(x) должны равняться size(v,1).
Пример: [1 2 3 4 5 6 7 8 9 10]
Пример: 1:10
Пример: [3 7 11 15 19 23 27 31]'
Типы данных: single | double | duration | datetime
v - Выборочные значенияЗначения выборки, заданные как вектор, матрица или массив вещественных или комплексных чисел. Если v является матрицей или массивом, то каждый столбец содержит отдельный набор 1-D значений.
Если v содержит комплексные числа, затем interp1 интерполирует действительную и мнимую части по отдельности.
Пример: rand(1,10)
Пример: rand(10,1)
Пример: rand(10,3)
Типы данных: single | double | duration | datetime
Поддержка комплексного номера: Да
xq - Точки запросаТочки запроса, заданные как скаляр, вектор, матрица или массив вещественных чисел.
Пример: 5
Пример: 1:0.05:10
Пример: (1:0.05:10)'
Пример: [0 1 2 7.5 10]
Типы данных: single | double | duration | datetime
method - Метод интерполяции'linear' (по умолчанию) | 'nearest' | 'next' | 'previous' | 'pchip' | 'cubic' | 'v5cubic' | 'makima' | 'spline'Метод интерполяции, указанный в качестве одного из параметров в этой таблице.
|
Метод |
Описание |
Непрерывность |
Комментарии |
|---|---|---|---|
|
|
Линейная интерполяция. Интерполированное значение в точке запроса основано на линейной интерполяции значений в соседних точках сетки в каждом соответствующем измерении. Это метод интерполяции по умолчанию. |
C0 |
|
|
|
Интерполяция ближайшего соседа. Интерполированное значение в точке запроса - это значение в ближайшей выборочной точке сетки. |
Прерывистый |
|
|
|
Интерполяция следующего соседа. Интерполированное значение в точке запроса - это значение в следующей выборочной точке сетки. |
Прерывистый |
|
|
|
Предыдущая интерполяция соседей. Интерполированное значение в точке запроса - это значение в предыдущей выборочной точке сетки. |
Прерывистый |
|
|
|
Фасонно-сохраняющая кусочно-кубическая интерполяция. Интерполированное значение в точке запроса основано на сохраняющей форму кусочно-кубической интерполяции значений в соседних точках сетки. |
C1 |
|
| Кубический сверток, используемый в MATLAB ® 5. |
C1 |
|
|
| То же, что и |
C1 | |
|
|
Модифицированная Akima кубическая эрмитовая интерполяция. Интерполированное значение в точке запроса основано на кусочной функции многочленов со степенью не более трех. Формула Акимы модифицируется, чтобы избежать переполнения. |
C1 |
|
|
|
Интерполяция сплайна с использованием условий конца без узла. Интерполированное значение в точке запроса основано на кубической интерполяции значений в соседних точках сетки в каждом соответствующем измерении. |
C2 |
|
extrapolation - Стратегия экстраполяции'extrap' | скалярное значениеСтратегия экстраполяции, указанная как 'extrap' или вещественное скалярное значение.
Определить 'extrap' когда вы хотите interp1 для вычисления точек за пределами области с помощью того же метода, который используется для интерполяции.
Укажите скалярное значение, когда необходимо interp1 возвращает определенное постоянное значение для точек за пределами области.
Поведение по умолчанию зависит от входных аргументов:
При указании 'pchip', 'spline', или 'makima' методы интерполяции, то поведение по умолчанию 'extrap'.
Все остальные методы интерполяции возвращаются NaN по умолчанию для точек запроса за пределами домена.
Пример: 'extrap'
Пример: 5
Типы данных: char | string | single | double
vq - Интерполированные значенияИнтерполированные значения, возвращаемые как скаляр, вектор, матрица или массив. Размер vq зависит от формы v и xq.
| Форма v | Форма xq | Размер Vq | Пример |
|---|---|---|---|
| Вектор | Вектор | size(xq) | Если size(v) = [1 100]и size(xq) = [1 500], тогда size(vq) = [1 500]. |
| Вектор | Матрица или массив N-D | size(xq) | Если size(v) = [1 100]и size(xq) = [50 30], тогда size(vq) = [50 30]. |
| Матрица или массив N-D | Вектор | [length(xq) size(v,2),...,size(v,n)] | Если size(v) = [100 3]и size(xq) = [1 500], тогда size(vq) = [500 3]. |
| Матрица или массив N-D | Матрица или массив N-D | [size(xq,1),...,size(xq,n),... size(v,2),...,size(v,m)] | Если size(v) = [4 5 6]и size(xq) = [2 3 7], тогда size(vq) = [2 3 7 5 6]. |
pp - Кусочный многочленКусочный многочлен, возвращенный как структура, которую можно передать ppval функция для оценки.
Алгоритм Акимы для одномерной интерполяции, описанный в [1] и [2], выполняет кубическую интерполяцию для получения кусочных многочленов с непрерывными производными первого порядка (С1). Алгоритм сохраняет наклон и избегает волнистости в плоских областях. Плоская область возникает всякий раз, когда существуют три или более последовательных коллинеарных точек, которые алгоритм соединяет прямой линией. Чтобы обеспечить плоскую область между двумя точками данных, вставьте дополнительную точку данных между этими двумя точками.
Когда встречаются две плоские области с разными уклонами, модификация, сделанная для исходного алгоритма Акимы, придает больший вес той стороне, где наклон ближе к нулю. Эта модификация отдает приоритет стороне, которая ближе к горизонтали, что более интуитивно и позволяет избежать перестрелки. (Исходный алгоритм Акимы даёт равные веса точкам с обеих сторон, таким образом равномерно деля волнообразную форму.)
С другой стороны, алгоритм сплайна выполняет кубическую интерполяцию для получения кусочных многочленов с непрерывными производными второго порядка (С2). Результат сравним с правильной полиномиальной интерполяцией, но менее подвержен сильным колебаниям между точками данных для высоких степеней. Тем не менее, этот метод может быть подвержен перегрузкам и колебаниям между точками данных.
По сравнению со сплайновым алгоритмом алгоритм Акимы производит меньше волнистостей и лучше подходит для борьбы с быстрыми изменениями между плоскими областями. Это различие иллюстрируется ниже с использованием тестовых данных, которые соединяют несколько плоских областей.
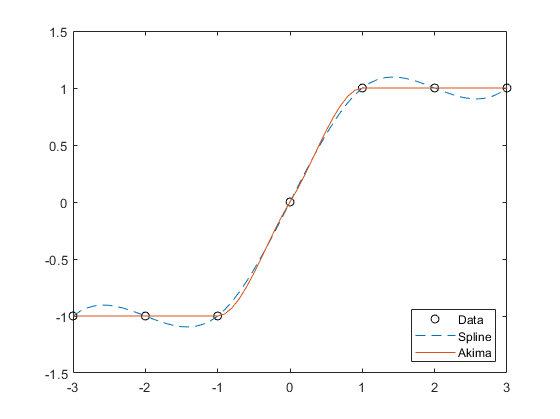
'cubic' способ interp1 выполняет кубический свертокВ R2020b изменилось поведение
В R2020b, 'cubic' метод интерполяции interp1 выполняет кубический сверток. 'v5cubic' и 'cubic' методы интерполяции теперь выполняют тот же тип интерполяции, что согласуется с поведением interp2, interp3, и interpn. Метод интерполяции кубических сверток предназначен для равномерно разнесенных данных и возвращается к 'spline' интерполяция для нерегулярно разнесенных данных.
В предыдущих выпусках 'cubic' было таким же, как 'pchip', и только 'v5cubic' выполнен кубический сверток.
[1] Акима, Хироси. «Новый метод интерполяции и сглаживания подгонки кривой на основе локальных процедур». Журнал ACM (JACM), 17.4, 1970, стр. 589-602.
[2] Акима, Хироси. «Метод двухмерной интерполяции и гладкой подгонки поверхности на основе локальных процедур». Сообщения АСМ, 17.1, 1974, стр. 18-20.
Примечания и ограничения по использованию:
Создание кода не поддерживает 'cubic' или 'makima' методы интерполяции.
Входной аргумент x (выборочные точки) должны быть строго увеличивающимися или строго уменьшающимися. Индексы не переупорядочены.
Если входной аргумент v (значения выборки) является вектором переменной длины (1-by-: или :-по-1), то форма выхода vq соответствует форме в MATLAB.
Если входной аргумент v является переменным размером, не является вектором переменной длины и становится вектором строки во время выполнения, после чего возникает ошибка.
Если входной аргумент xq (точки запроса) - переменный размер, не является вектором переменной длины и становится вектором строки или столбца во время выполнения, после чего возникает ошибка.
См. раздел Ограничения размера переменной для создания кода функций панели инструментов (кодер MATLAB).
Примечания и ограничения по использованию:
Создание кода не поддерживает 'cubic' или 'makima' методы интерполяции.
Входной аргумент x (выборочные точки) должны быть строго увеличивающимися или строго уменьшающимися. Индексы не переупорядочены.
Если входной аргумент v (значения выборки) является вектором переменной длины (1-by-: или :-по-1), то форма выхода vq соответствует форме в MATLAB.
Если входной аргумент v является переменным размером, не является вектором переменной длины и становится вектором строки во время выполнения, после чего возникает ошибка.
Если входной аргумент xq (точки запроса) - переменный размер, не является вектором переменной длины и становится вектором строки или столбца во время выполнения, после чего возникает ошибка.
См. раздел Ограничения размера переменной для создания кода функций панели инструментов (кодер MATLAB).
Примечания и ограничения по использованию:
method должно быть 'linear', 'nearest', 'cubic', 'v5cubic', или 'spline'.
Дополнительные сведения см. в разделе Запуск функций MATLAB на графическом процессоре (панель инструментов параллельных вычислений).
Эта функция полностью поддерживает распределенные массивы. Дополнительные сведения см. в разделе Запуск функций MATLAB с распределенными массивами (панель инструментов параллельных вычислений).
Имеется измененная версия этого примера. Открыть этот пример с помощью изменений?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.