Векторные объемные данные содержат больше информации, чем скалярные данные, поскольку каждая точка координат в наборе данных имеет три связанных с ней значения. Эти значения определяют вектор, который представляет как величину, так и направление. Скорость потока текучей среды является примером векторных данных.
Для визуализации векторных данных используется ряд методов:
Линии потока отслеживают путь, по которому будет следовать безмассовая частица, погруженная в векторное поле.
Частицы потока - это маркеры, отслеживающие линии потока и используемые для создания анимации линий потока.
Ленты потока подобны линиям потока, за исключением того, что ширина лент позволяет им указывать на скручивание. Ленты потока полезны для указания угловой скорости завитка.
Трубы потока аналогичны линиям потока, но можно также управлять шириной трубы. Поточные трубки полезны для отображения расхождения векторного поля.
Графики конуса представляют величину и направление данных в каждой точке, отображая коническую стрелку или стрелку.
Обычно эти функции лучше всего объясняют данные при использовании в сочетании с другими методами визуализации, такими как контуры, секущие плоскости и изоповерхности. Примеры в этом разделе иллюстрируют некоторые из этих методов.
Методы визуализации, такие как контурные срезы, плоскости среза и изо-поверхности, требуют скалярных данных объема. Эти методы можно использовать с векторными данными, беря величину векторов. Например, wind набор данных возвращает три массива координат и три массива векторных компонентов, u, v, w. В этом случае величина векторов скорости равна скорости ветра в каждой соответствующей точке координат в объеме.
wind_speed = sqrt(u.^2 + v.^2 + w.^2);
Множество wind_speed содержит скалярные значения для данных тома. Полезность информации, получаемой с помощью этого подхода, однако, зависит от того, какое физическое явление представлено величиной векторных данных.
Графики потока (линии потока, ленты, трубы и конусы или стрелки) иллюстрируют поток векторного поля 3-D. Функции печати потока MATLAB ® (streamline, streamribbon, streamtube, coneplot, stream2, stream3) требуется указать точку, в которой необходимо начать трассировку каждого потока.
Как правило, знание характеристик данных помогает выбрать исходные точки. Информация, такая как основное направление потока и диапазон координат данных, помогает определить, где оценивать данные.
streamslice функция полезна для изучения данных. Например, эти операторы рисуют фрагмент через векторное поле со значением z посередине в диапазоне.
load wind zmax = max(z(:)); zmin = min(z(:)); streamslice(x,y,z,u,v,w,[],[],(zmax-zmin)/2)
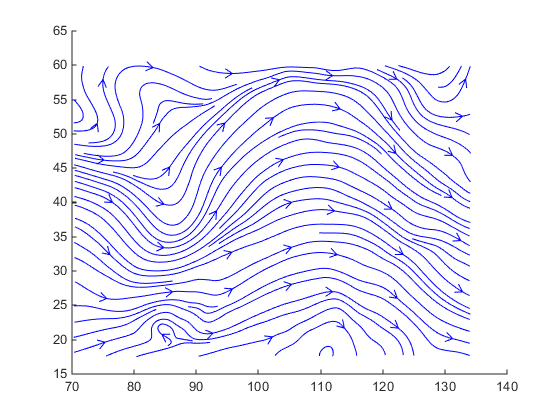
Этот график среза потока показывает, что поток находится в положительном направлении x, а также позволяет выбрать начальные точки как в x, так и в y. Можно создать похожие графики, разделяющие объем в плоскости x-z или плоскости y-z, чтобы получить дополнительное представление о диапазоне и ориентации данных.
Чтобы задать начальную точку для одной линии потока, необходимы координаты точки x, y и z. meshgrid предоставляет удобный способ создания массивов начальных точек. Например, можно выбрать следующие начальные точки из данных ветра, отображаемых в предыдущем срезе потока.
[sx,sy,sz] = meshgrid(80,20:10:50,0:5:15);
Это утверждение определяет начальные точки как все лежащие на x = 80, y в диапазоне от 20 до 50 и z в диапазоне от 0 до 15. Вы можете использовать plot3 для отображения расположений.
plot3(sx(:),sy(:),sz(:),'*r'); axis(volumebounds(x,y,z,u,v,w)) grid on set(gca,'BoxStyle','full','Box','on') daspect([2 2 1])
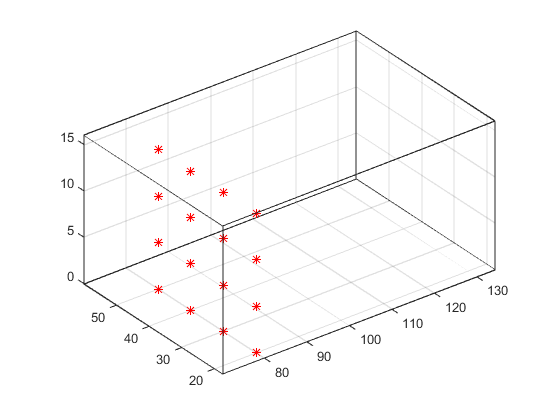
Нет необходимости использовать 3-D массивы, например, возвращенные meshgrid, но размер каждого массива должен быть одинаковым, и meshgrid предоставляет удобный способ создания массивов, когда в каждой координате отсутствует одинаковое количество уникальных значений. Можно также определить массивы начальных точек как векторы столбцов. Например, meshgrid возвращает 3-D массивы:
[sx,sy,sz] = meshgrid(80,20:10:50,0:5:15); whos
Name Size Bytes Class Attributes sx 4x1x4 128 double sy 4x1x4 128 double sz 4x1x4 128 double
Кроме того, можно использовать векторы столбцов 16 на 1 с соответствующими элементами трех массивов, составляющими координаты каждой начальной точки. (Это эквивалент индексации значений, возвращаемых meshgrid как sx(:), sy(:), и sz(:).)
Например, добавление линий потока к начальным точкам приводит к следующему:
streamline(x,y,z,u,v,w,sx(:),sy(:),sz(:))
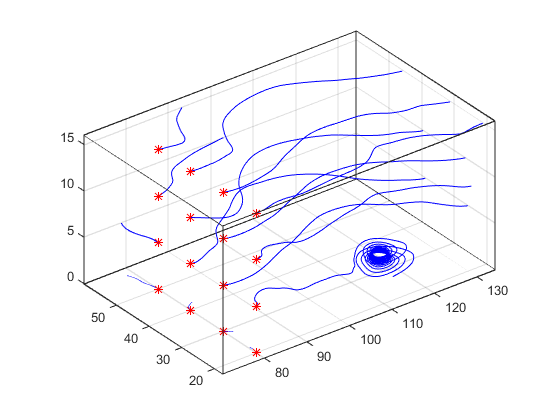
subvolume функция обеспечивает простой способ доступа к субрегионам набора данных тома. subvolume позволяет выбирать интересующие области на основе пределов, а не использовать оператор двоеточия для индексации в массивы 3-D, определяющие тома. Рассмотрим следующие два подхода к созданию данных для субтома: индексирование с помощью оператора двоеточия и использование subvolume.
При индексации массивов используются значения, определяющие элементы в каждом измерении массива.
load wind xsub = x(1:10,20:30,1:7); ysub = y(1:10,20:30,1:7); zsub = z(1:10,20:30,1:7); usub = u(1:10,20:30,1:7); vsub = v(1:10,20:30,1:7); wsub = w(1:10,20:30,1:7);
subvolume позволяет использовать значения координат, которые можно считывать по осям. Например:
lims = [100.64 116.67 17.25 28.75 -0.02 6.86]; [xsub,ysub,zsub,usub,vsub,wsub] = subvolume(x,y,z,u,v,w,lims);
Затем можно использовать данные субобъема в качестве входных данных для любой функции, требующей векторных объемных данных.