Радиальная базисная функция имеет вид
где x - n-мерный вектор,
является n-мерным вектором, называемым центром радиальной базисной функции, | |. | | обозначает евклидово расстояние и является одномерной функцией, определяемой для положительных входных значений, которую мы будем называть функцией профиля .
Модель строится как линейная комбинация N радиальных базисных функций с N отдельными центрами. Учитывая входной вектор x, выходной сигнал сети RBF является вектором активности
, задаваемым
где
- вес, связанный с j-й радиальной базовой функцией, центрированной на, 
и. 
Выходной сигнал
аппроксимирует целевой набор значений, обозначенных y.
В MBC имеется множество радиальных базисных функций, каждая из которых характеризуется формой. 
Все радиальные базовые функции также имеют связанный параметр ширины, 
который связан с расширением функции вокруг ее центра. Выбор поля в настройке модели обеспечивает настройку ширины по умолчанию. Ширина по умолчанию - это среднее значение по центрам расстояния от каждого центра до ближайшего соседа. Это эвристика, данная в Hassoun (см. Ссылки) для гауссов, но это только грубое руководство, которое предоставляет начальную точку для алгоритма выбора ширины.
Другим параметром, связанным с радиальными базисными функциями, является параметр регуляризации. 
Этот (обычно небольшой) положительный параметр используется в большинстве алгоритмов подгонки. Параметр
штрафует за большие веса, которые имеют тенденцию производить более плавные приближения y и уменьшать тенденцию сети к перевыполнению (то есть хорошо соответствовать целевым значениям y, но иметь плохую прогностическую способность).
В следующих разделах описываются различные параметры радиальных базовых функций, доступных в изделии Калибровка на основе модели (Model-Based Calibration Toolbox™), и способы их использования для моделирования.
В диалоговом окне Настройка модели (Model Setup) можно выбрать ядро RBF для использования. Ядра - это типы RBF (мультиквадрические, гауссовы, тонкослойные и так далее). Эти типы описаны в следующих разделах.
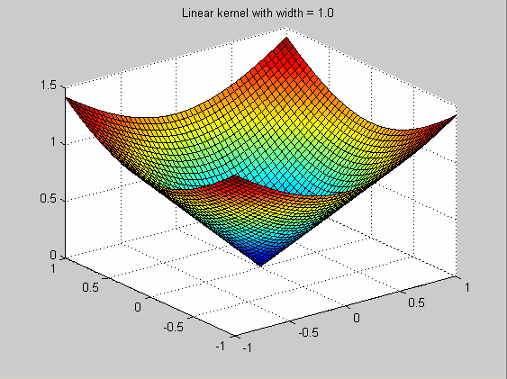
Это радиальная базовая функция, наиболее часто используемая в нейронном сетевом сообществе. Функция профиля:
Это приводит к радиальной базовой функции
В этом случае параметр width совпадает со стандартным отклонением гауссовой функции.
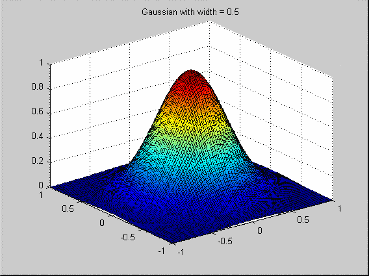
Эта радиальная базисная функция является примером сглаживающего сплайна, популяризированного Грейс Вахбой (Grace Wahba) (http://www.stat.wisc.edu/~wahba/). Обычно они дополняются многочленами низкого порядка. Функция профиля:
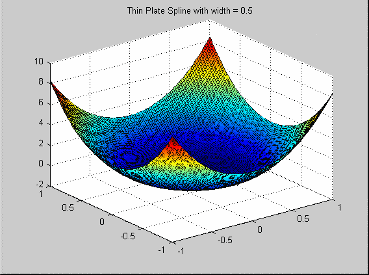
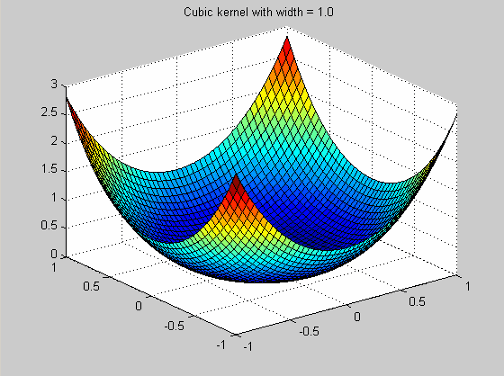
Эти радиальные базисные функции упоминаются в Hassoun (см. Ссылки). Они имеют функцию профиля
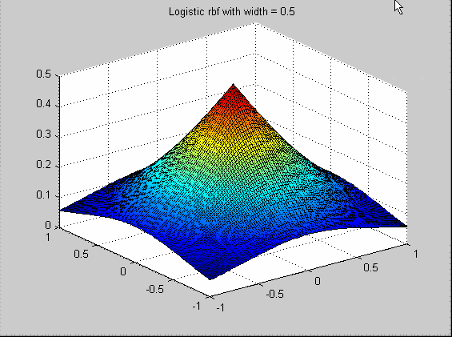
Они образуют семейство радиальных базисных функций, которые имеют кусочно-полиномиальную функцию профиля и компактную поддержку [Wendland, см. Ссылки]. Выбираемый член семейства зависит от размера пространства (n), из которого выводятся данные, и желаемой степени непрерывности многочленов.
| Измерение | Непрерывность | Профиль |
|---|---|---|
n = 1 | 0 |
|
2 |
| |
4 |
| |
n = 3 | 0 |
|
2 | + (4r + 1) | |
4 |
| |
n = 5 | 0 |
|
2 |
| |
4 |
|
Мы использовали нотацию
для положительной части a.
Если n равно четному, используется радиальная базисная функция, соответствующая размеру n + 1.
Заметим, что каждая из радиальных базисных функций ненулевая, когда r находится в [0,1]. Можно изменить опору, заменяя
r
на в предыдущей формуле. Параметр
по-прежнему называется шириной радиальной базовой функции.
Аналогичные формулы для функций профиля существуют для n > 5 и для четной непрерывности > 4. Функции Вендланда доступны вплоть до чётной непрерывности 6, и в любом пространственном измерении n.
Примечания по использованию
Лучшие свойства аппроксимации обычно связаны с более высокой непрерывностью.
Для данного набора данных параметр width для функций Вендланда должен быть больше ширины, выбранной для гауссова.
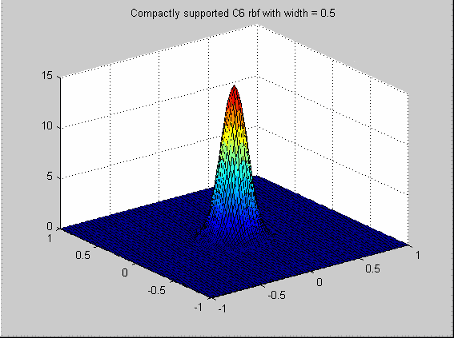
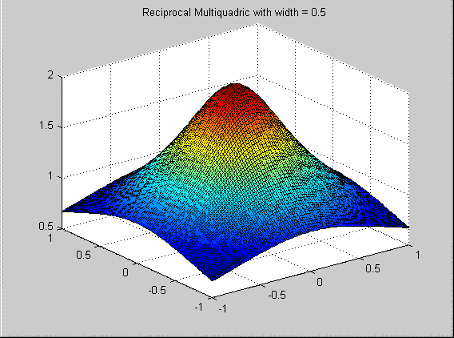
Это популярный инструмент для выборочной подстройки данных. Они имеют функцию профиля
.
Они имеют функцию профиля.
Обратите внимание, что нулевая ширина
недопустима.
Они имеют функцию профиля.
Они имеют функцию профиля.
Существует четыре характеристики РФБ, которые необходимо решить: веса, центры, ширина и. 
Каждый из них может оказать значительное влияние на качество результирующей посадки, и для каждого из них необходимо определить хорошие значения. Веса всегда определяются заданием центров, ширины и, 
а затем решением соответствующей линейной системы уравнений. Однако задача определения хороших центров, ширины и в
первую очередь далеко не проста, и осложняется сильными зависимостями между параметрами. Например, оптимум
значительно изменяется при изменении параметра ширины. Глобальный поиск по всем возможным центровым расположениям, ширине и является
с точки зрения вычислений запредельным во всех ситуациях, кроме простейших.
Чтобы попытаться бороться с этой проблемой, процедуры подгонки идут на трех различных уровнях.
На самом низком уровне находятся алгоритмы, которые выбирают соответствующие центры для заданных значений ширины и. 
Центры выбираются по одному из набора кандидатов (обычно набор точек данных или их подмножество). Поэтому полученные центры ранжируются в приблизительном порядке важности.
На среднем уровне находятся алгоритмы, которые выбирают соответствующие значения для
центров и, учитывая заданную ширину.
На верхнем уровне находятся алгоритмы, которые стремятся найти хорошие значения для каждого из центров, ширины и. 
Эти алгоритмы верхнего уровня проверяют различные значения ширины. Для каждого значения ширины вызывается один из алгоритмов среднего уровня, определяющий хорошие центры и значения для.
Эти алгоритмы и их параметры подгонки описаны в следующих разделах:
Это основной алгоритм, как описано в Chen, Chng и Alkadhimi [См. Ссылки]. В Rols (Регуляризованные ортогональные наименьшие квадраты) центры выбирают по одному из набора кандидатов, состоящего из всех точек данных или их подмножества. Он выбирает новые центры в процедуре выбора вперед. Начиная с нулевых центров, на каждом шаге выбирается центр, уменьшающий регуляризованную ошибку. На каждом этапе регрессионная матрица X разлагается с использованием алгоритма Грама-Шмидта на произведение X = WB, где W имеет ортогональные столбцы и B является верхней треугольной с единицами на диагонали. По своей природе это похоже на QR-разложение. Регуляризованная ошибка задается значением
, где g = Bw, а e - остаток, определяемый значением. 
Минимизация регуляризованной ошибки делает сумму квадратной ошибки
малой, в то же время не позволяя получить
слишком большой. Поскольку g соотносится с весами по g = Bw, это приводит к удерживанию весов под контролем и уменьшению перегонки. Для
повышения эффективности используется термин, а не сумма квадратов весов.
Алгоритм завершается либо при достижении максимального количества центров, либо добавление новых центров не приводит к значительному снижению коэффициента регуляризованных ошибок (контролируется пользовательским допуском).
Параметры подгонки. Максимальное количество центров - максимальное количество центров, которое может выбрать алгоритм. Значение по умолчанию - это меньшее из 25 центров или δ числа точек данных. Формат: min(nObs/4, 25). Можно ввести значение (например, при вводе 10 создается десять центров) или отредактировать существующую формулу (например, (nObs/2, 25) создает половину числа точек данных или 25, в зависимости от того, что меньше).
Процент данных, которые должны быть центрами-кандидатами - процент точек данных, которые должны использоваться в качестве центров-кандидатов. Это определяет подмножество точек данных, которые формируют пул для выбора центров. По умолчанию используется значение 100%, т.е. все точки данных рассматриваются как новые центры. Это может быть уменьшено для ускорения времени выполнения.
Регуляризованный допуск ошибок (Regularized error tolerance) - управляет количеством центров, выбранных до остановки алгоритма. Для получения подробной информации см. Chen, Chng и Alkadhimi [Ссылки]. Этот параметр должен быть положительным числом от 0 до 1. Большие допуски означают, что выбирается меньше центров. Значение по умолчанию - 0,0001. Если выбрано меньше максимального количества центров и требуется принудительно выбрать максимальное число, уменьшите допуск до эпсилона (eps).
RedErr означает уменьшенную ошибку. Этот алгоритм также начинается с нулевых центров и выбирает центры в процедуре прямого выбора. Алгоритм находит (среди ещё не выбранных точек данных) точку данных с наибольшим остатком и выбирает эту точку данных в качестве следующего центра. Этот процесс повторяется до тех пор, пока не будет достигнуто максимальное количество центров.
Параметры подгонки. Только имеет количество центров.
Этот алгоритм основан на эвристике, что следует поместить больше центров в область, где есть больше вариаций остатка. Для каждой точки данных набор соседей идентифицируется как точки данных на расстоянии sqrt (nf), деленном на максимальное количество центров, где nf - количество факторов. Вычисляют средние остатки в наборе соседей, затем определяют величину колебания остатка в области этой точки данных как сумму квадратов разностей между остатком в каждом соседе и средними остатками соседей. Точка данных с наибольшим колебанием выбирается следующим центром.
Параметры подгонки. Почти как в Rols алгоритм, за исключением отсутствия регуляризованной ошибки.
Этот алгоритм берет концепцию из оптимального дизайна экспериментов и применяет ее к задаче выбора центра в радиальных базисных функциях. Набор центров-кандидатов генерируется латинским гиперкубом, методом, обеспечивающим квазиоднородное распределение точек. Из этого набора кандидатов n центров выбираются случайным образом. Это множество дополняется p новыми центрами, затем это множество n + p центров уменьшается до n путем итеративного удаления центра, который дает лучшую статистику PRESS (как в пошаговом режиме). Этот процесс повторяется количество раз, указанное в поле Количество циклов увеличения/уменьшения.
CentreExchange и Tree Regression (см. Регрессия дерева) - это единственные алгоритмы, разрешающие центры, которые не расположены в точках данных. Это означает, что центры на графиках модели не отображаются. CentreExchange алгоритм может быть более гибким, чем другие алгоритмы выбора центров, которые выбирают центры как подмножество точек данных; однако это значительно больше времени и не рекомендуется для более крупных проблем.
Параметры подгонки. Количество центров - количество центров, которые будут выбраны
Количество циклов увеличения/уменьшения - количество операций увеличения, а затем уменьшения центрального набора
Количество центров для увеличения - сколько центров для увеличения
Лямбда - параметр регуляризации.
Для заданной ширины этот алгоритм оптимизирует параметр регуляризации относительно критерия GCV (обобщенная перекрестная проверка; см. обсуждение в рамках критерия GCV).
Начальные центры либо выбираются одним из низкоуровневых алгоритмов выбора центров, либо используется предыдущий выбор центров (см. обсуждение под параметром Do not reselect centers). Начальное начальное значение можно выбрать
путем тестирования начального количества значений лямбда (установленных пользователем), которые равномерно разнесены по логарифмической шкале между 10-10 и 10, и выбора значения с лучшим баллом GCV. Это помогает избежать попадания в локальные минимумы на
кривой GCV.
Затем этот параметр итерируется, чтобы попытаться минимизировать GCV с помощью формул, приведенных в разделе критерия GCV. Итерация останавливается при достижении максимального количества обновлений или при изменении значения log10 (GCV) меньше допуска.
Параметры подгонки. Алгоритм выбора центра - используемый алгоритм выбора центра.
Максимальное количество обновлений - максимальное количество обновлений
. Значение по умолчанию - 10.
Минимальное изменение в log10 (GCV) - допуск. Это определяет критерий остановки для итерации
; обновление останавливается, когда разница в значении log10 (GCV) меньше допуска. Значение по умолчанию - 0,005.
Количество начальных тестовых значений для лямбда - количество тестовых значений
для определения начального значения для. 
Установка для этого параметра значения 0 означает, что на данный
момент используется наилучший вариант.
Не следует повторно выбирать центры для новой ширины - этот флажок определяет, будут ли центры повторно выбраны для нового значения ширины и после каждого обновления лямбды или же будут использоваться лучшие центры на сегодняшний день. Дешевле сохранить лучшие центры, найденные до сих пор, и часто этого достаточно, но это может вызвать преждевременную сходимость к конкретному набору центров.
Показать (Display) - при установке этого флажка этот алгоритм отображает результаты алгоритма. Начальная точка для
помечена черным кругом. После
обновления новые значения отображаются как красные крестики, соединенные красными линиями. Лучший
найденный отмечен зеленой звездочкой.
Если скорее всего будет создано слишком много графиков, из-за того, что здесь установлен флажок Показать (Display), генерируется предупреждение, и можно остановить выполнение.
Нижняя граница 10-12 располагается на, 
а верхняя граница 10.
Для указанной ширины этот алгоритм оптимизирует параметр регуляризации в Rols алгоритм по критерию GCV. Начальная посадка и центры выбираются Rols используя предоставленный пользователем. 
Как в IterateRidge, вы выбираете начальное начальное значение для
, тестируя начальное число начальных значений лямбды, которые равномерно разнесены по логарифмической шкале между 10-10 и 10, и выбирая то, которое имеет лучший балл GCV.
затем итерируется для улучшения GCV. При каждом
обновлении процесс выбора центра повторяется. Это означает, что IterateRols гораздо дороже в вычислительном отношении, чем IterateRidge.
Нижняя граница 10-12 располагается на, 
а верхняя граница 10.
Параметры подгонки. Алгоритм выбора центра - используемый алгоритм выбора центра. Для IterateRols единственным доступным алгоритмом выбора центра является Rols.
Максимальное количество обновлений - то же, что и для IterateRidge.
Минимальное изменение log10 (GCV) - то же, что и дляIterateRidge.
Количество начальных испытательных значений для лямбда - то же, что и для IterateRidge.
Не следует повторно выбирать центры для новой ширины - этот флажок определяет, будут ли повторно выбраны центры для нового значения ширины или будут использоваться лучшие центры на сегодняшний день.
Показать (Display) - при установке этого флажка этот алгоритм отображает результаты алгоритма. Начальная точка для
помечена черным кругом.
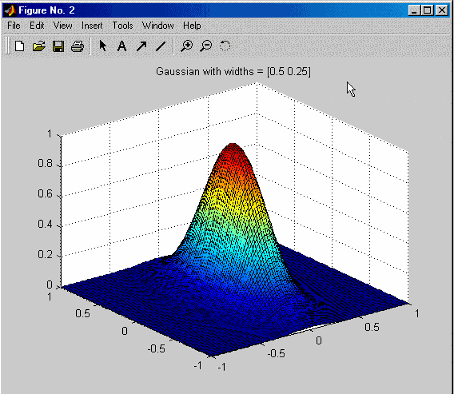
По мере обновления приведенного выше рисунка новые значения отображаются в виде красных крестиков, соединенных красными линиями. Лучший
найденный отмечен зеленой звездочкой.
Если скорее всего будет создано слишком много графиков, из-за того, что здесь установлен флажок Показать (Display), генерируется предупреждение, и можно остановить выполнение.
Этот алгоритм объединяет процессы выбора центра и лямбда-выбора. Вместо того, чтобы ждать, пока все центры будут выбраны до
обновления (как и другие лямбда-алгоритмы выбора), этот алгоритм предлагает возможность обновления
после выбора каждого центра. Это алгоритм прямого выбора, который, как Rols, выбирает центры на основе регуляризованного уменьшения ошибок. Критерий остановки для StepItRols является на основе изменения log10 (GCV) менее чем на допуск более чем заданное число раз подряд (указанное в параметре Максимальное число раз изменения log10 (GCV) минимально). После прекращения добавления центров выбирается промежуточная посадка с наименьшим log10 (GCV). Это может включать в себя удаление некоторых центров, которые были введены с опозданием в алгоритм.
Параметры подгонки. Максимальное количество центров - как в Rols алгоритм.
Процент данных в центры-кандидаты - как в Rols алгоритм.
Количество центров, добавляемых перед обновлением - сколько центров выбрано перед
началом итерации.
Минимальное изменение в log10 (GCV) - допуск. Оно должно быть положительным числом от 0 до 1. Значение по умолчанию - 0,005.
Максимальное число изменений log10 (GCV) минимально - управляет количеством центров, выбранных перед остановкой алгоритма. Значение по умолчанию - 5. Если оставить значение по умолчанию, выбор центра останавливается, когда значения log10 (GCV) изменяются меньше допуска пять раз подряд.
Эта подпрограмма проверяет несколько значений ширины с помощью различных значений ширины. Выбирают набор пробных значений ширины, равномерно распределенных между указанными начальными верхним и нижним границами. Выбирается ширина с наименьшим значением log10 (GCV). Область вокруг лучшей ширины затем тестируется более подробно - это называется zoom. В частности, новый диапазон пробных значений ширины центрируется по лучшей ширине, найденной в предыдущем диапазоне, и длина интервала, из которого выбраны значения ширины, уменьшается до 2/5 длины интервала при предыдущем увеличении. Перед тестированием нового набора значений ширины пробной версии выбор центра обновляется, чтобы отразить наилучшую ширину и
найденную на данный момент. Это может означать, что расположение оптимальной ширины изменяется между увеличениями из-за новых центральных расположений.
Параметры подгонки. Лямбда-алгоритм выбора - алгоритм подгонки среднего уровня, который тестируется с различными пробными значениями. 
Значение по умолчанию: IterateRidge.
Количество значений ширины пробной версии в каждом масштабе - количество пробных версий, выполненных при каждом масштабе. Испытываемые ширины равномерно разнесены между начальным верхним и нижним границами. Значение по умолчанию - 10.
Количество увеличений - количество увеличений. Значение по умолчанию - 5.
Начальная нижняя граница по ширине - нижняя граница по ширине для первого масштабирования. Значение по умолчанию - 0,01.
Начальная верхняя граница по ширине - верхняя граница по ширине для первого масштабирования. Значение по умолчанию - 20.
Показать (Display) - если этот флажок установлен, будет выведен основной график log10 (GCV) относительно ширины. Наилучшая ширина отмечена зеленой звездочкой.
В WidPerDim (Width Per Dimension), радиальные базисные функции обобщены. Вместо одного параметра ширины можно использовать различную ширину в каждом входном коэффициенте; то есть кривые уровня являются эллиптическими, а не круглыми (или сферическими, с большим количеством факторов). Базовые функции более не являются радиально симметричными.
Это может быть особенно полезным, когда величина изменчивости значительно изменяется в каждом направлении ввода. Этот алгоритм обеспечивает большую гибкость, чем TrialWidths, но является более дорогостоящим в вычислительном отношении.
Можно задать начальную ширину в элементах управления RBF в диалоговом окне Настройка глобальной модели (Global Model Setup). Для большинства алгоритмов начальная ширина является единственным значением. Однако для WidPerDim (доступно в раскрывающемся списке Алгоритм выбора ширины) можно указать вектор ширины, который будет использоваться в качестве начальной ширины.
При предоставлении вектора ширины должно быть то же число, что и число глобальных переменных, и они должны быть в том же порядке, что и указано в плане тестирования. Если задана одна ширина, то все размеры начинаются с одной и той же начальной ширины, но, вероятно, будут перемещаться оттуда к вектору ширины во время фитинга модели.
Вычисляют оценку времени для алгоритма ширины на размерность. Это задается как количество единиц времени (так как это зависит от машины). Оценка времени более 10, но менее 100 генерирует предупреждение. Оценка времени более 100 может занять слишком много времени (вероятно, более пяти минут на большинстве машин). Имеется возможность остановить выполнение и изменить некоторые параметры для сокращения времени выполнения.
Параметры подгонки. Что касается TrialWidths алгоритм.
Алгоритм регрессии дерева для RBF состоит из трех частей:
Здание дерева. Алгоритм регрессии дерева строит дерево регрессии из данных и использует узлы (или панели) этого дерева для вывода центров-кандидатов и ширины для RBF. Корневая панель дерева соответствует гиперкубу, который содержит все точки данных. Эта панель разделена на две дочерние панели, так что каждый дочерний элемент содержит одинаковую величину вариации, насколько это возможно. Дочерняя панель с наибольшей вариацией затем разделяется аналогичным образом. Этот процесс продолжается до тех пор, пока не останется ни одной панели для разделения, т.е. ни одна дочерняя панель не будет иметь больше, чем минимальное количество точек данных, или пока не будет достигнуто максимальное количество панелей. Каждая панель в дереве соответствует центру-кандидату, и размер панели определяет ширину, которая соответствует этому вектору.
Размер дочерних панелей может быть основан исключительно на размере родительской панели или может быть определен путем сжатия дочерней панели на данные, которые она содержит.
После выбора Radial Basis Function в диалоговом окне Настройка глобальной модели (Global Model Setup) можно выбрать Tree Regression в раскрывающемся меню «Алгоритм выбора ширины».
Нажмите кнопку Дополнительно (Advanced), чтобы открыть диалоговое окно Опции радиальных базовых функций (Radial Basis Functions Options), чтобы получить такие настройки, как максимальное количество панелей и минимальное количество точек данных на панель. Чтобы сжать дочерние панели в соответствии с данными, установите флажок «Сжать панели до данных».
Алгоритм выбора альфа-канала. Размер для ширины кандидата не берется непосредственно из размеров панели: нам нужно масштабировать размеры панели, чтобы получить соответствующую ширину. Этот коэффициент масштабирования называется альфа. Тот же коэффициент масштабирования должен применяться к каждой панели в дереве, и для определения оптимального значения альфа мы используем алгоритм выбора альфа.
Можно выбрать параметр Specify Alpha чтобы указать точное значение альфа для использования, или можно выбрать Trial Alpha. Trial Alphaочень похож на алгоритм Trial Widths. Единственное отличие состоит в том, что пробный альфа-алгоритм может указать, как разместить значения для поиска. Linear является таким же, как используется при испытании ширины, но Logarithmic ищет больше значений в нижнем диапазоне.
Нажмите кнопку Дополнительно (Advanced), чтобы открыть диалоговое окно Опции радиальных базисных функций (Radial Basis Functions Options), чтобы получить дополнительные настройки, такие как границы альфа-канала, количество масштабов и количество пробных альфас. Здесь можно установить флажок Display для просмотра хода выполнения алгоритма и значений альфа-канала.
Алгоритм выбора центра. Дерево создает центры-кандидаты, а альфа-выбор создает для этих центров ширину кандидатов. При выборе центра выбирается, какой из этих центров использовать.
Generic Center Selection - алгоритм выбора центра, который не знает ничего об используемой древовидной структуре. Он использует Rols, что является очень быстрым способом выбора центров и работает в этом случае, а также в обычных случаях РФБ. Однако в этом случае кандидаты в центры не являются данными центров из регрессионного дерева.
Tree-based center selection использует дерево регрессии. Естественно использовать дерево регрессии для выбора центров из-за способа его построения. В частности, панель, соответствующая корневому узлу, должна рассматриваться для выбора перед любым из его нижестоящих элементов, так как она захватывает грубую детализацию, в то время как узлы в листьях дерева захватывают тонкую детализацию. Это то, что Tree-based center selection делает. Можно также задать максимальное количество центров.
Щелкните Дополнительно (Advanced), чтобы открыть диалоговое окно Опции радиальных базисных функций (Radial Basis Functions Options), чтобы достичь параметра Критерии выбора модели (Model selection criter Критерии выбора модели определяют, какую функцию следует использовать в качестве показателя качества модели. Это может быть BIC (байесовский информационный критерий) или GCV (обобщенная перекрестная проверка). БИК обычно менее подвержен чрезмерной примерке.
Меню Пошаговая (Stepwise) одинаково для всех RBF. См. раздел Класс глобальной модели: радиальная базисная функция.
Регрессия дерева и CentreExchange - это единственные алгоритмы, разрешающие центры, которые не расположены в точках данных. Это означает, что центры на графиках модели не отображаются.
Если оставить алгоритм выбора альфа по умолчанию, Trial Alphaпри нажатии кнопки «ОК» для начала моделирования появится диалоговое окно хода выполнения. Показан пример.
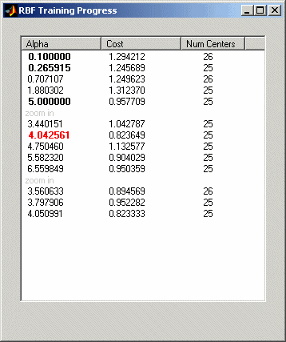
Это пример диалогового окна выполнения выполняемого фитинга модели RBF регрессии дерева. Здесь можно увидеть каждое пробное значение альфа с его рассчитанной стоимостью и лучшим количеством центров с этим значением альфа. Альфа-значение в красном - лучшее на данный момент. Альфа-значения больше не красные, а выделены жирным шрифтом, являются предыдущими лучшими значениями. Затем можно уточнить модель, увеличив оптимальные значения для альфа-центров и количества центров.
Справка: М. Орр, Дж. Халлам, К. Такезава, А. Мюррей, С. Ниномия, М. Ойде, Т. Леонард, «Объединение регрессионных деревьев и радиальных базовых функциональных сетей», Международный журнал нейронных систем, том 10, № 6 (2000) 453-465.
Функцию Prune можно использовать для уменьшения числа центров в сети радиальных базисных функций. Это помогает решить, сколько центров необходимо.
Для использования средства Prune:
Выберите глобальную модель RBF в дереве модели.
Нажмите кнопку на панели инструментов или выберите пункт меню Модель > Утилиты > Обрезать.
Появится диалоговое окно Выбор количества центров (Number of Centers Selector).
Графики показывают, как качество соответствия сети увеличивается по мере добавления большего количества RBF. Он использует тот факт, что большинство алгоритмов выбора центра являются жадными по своей природе, и поэтому порядок, в котором были выбраны центры, примерно отражает порядок важности базовых функций.
Критериями подгонки по умолчанию являются логарифмы PRESS, GCV, RMSE и Weighted PRESS. Дополнительные параметры определяются выбором в окне Сводная статистика. Взвешенная ПРЕССА штрафует за наличие большего числа центров, и выбор количества центров для минимизации взвешенной ПРЕССЫ часто является хорошим вариантом.
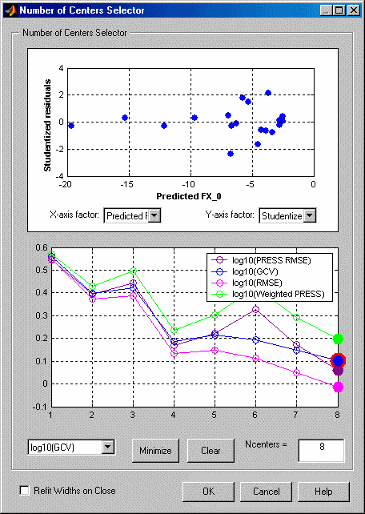
Все четыре критерия в этом типичном примере указывают на один и тот же минимум в восьми центрах.
Если все графы уменьшаются, как в предыдущем примере, это говорит о том, что максимальное количество центров слишком мало, и число центров должно быть увеличено.
При нажатии кнопки Свернуть (Minimize) выбирается количество центров, которое минимизирует критерий, выбранный в раскрывающемся меню слева. Хорошо, если это значение также минимизирует все остальные критерии. Кнопка «Очистить» возвращается к предыдущему выделению.
Следует отметить, что при уменьшении числа центров с помощью функции Prune корректируются только линейные параметры (веса RBF). Нелинейные параметры (расположение центра, ширина и лямбда) не корректируются. При выходе из диалогового окна можно выполнить рефит дешевой ширины, установив флажок Refit widths on close. Если сеть была значительно обрезана, следует использовать кнопку Обновить модель (Update Model Fit) на панели инструментов. При этом выполняется полное преобразование всех параметров.
Пусть A является матрицей, так что веса задаются
, где X является матрицей регрессии. Форма А варьируется в зависимости от используемого основного алгоритма подгонки.
В случае обычных наименьших квадратов мы имеем A = X 'X.
Для регрессии гребня (с параметром регуляризации) 
A задается A = X 'X + I
Далее - алгоритм Ролса. Во время алгоритма Ролса X разлагается с использованием алгоритма Грама-Шмидта, чтобы дать X = WB, где W имеет ортогональные столбцы, а B является верхней треугольной. Затем получают соответствующую матрицу A для Rols.
Матрица
называется hat-матрицей, и леверидж i-й точки данных hi задается i-м диагональным элементом H. Все статистические данные, полученные из hat-матрицы, например, PRESS, изученные остатки, доверительные интервалы и расстояние Кука, вычисляются с использованием hat-матрицы, соответствующей конкретному алгоритму аппроксимации.
Аналогичным образом PEV, приведенный в терминах и определениях статистики инструментария как
становится
ПЭВ вычисляется с использованием формы А, соответствующей конкретному алгоритму аппроксимации (обычные наименьшие квадраты, гребни или роли).
Обобщенная перекрестная проверка (GCV) - это мера достоверности соответствия модели данным, которая минимизируется, когда остатки малы, но не настолько малы, чтобы сеть перевыполнила данные. Его легко вычислить, и сети с небольшими значениями GCV должны иметь хорошую прогностическую способность. Он связан со статистикой PRESS.
Определение GCV дано Орром (4, см. Ссылки).
где y - целевой вектор, N - число наблюдений, а P - проекционная матрица, заданная I - XA-1XT. Определение А. см. в разделе Статистика.
Важной особенностью использования GCV в качестве критерия для определения оптимальной сети в наших алгоритмах подгонки является наличие формул обновления для параметра регуляризации. 
Эти формулы обновления получают путем дифференцирования GCV относительно
и установки результата на ноль. То есть они основаны на градиенте-спуске.
Это дает общее уравнение (от Orr, 6, References)
Теперь мы специализируем эти формулы на случае регрессии хребта и на алгоритме Ролса.
Показано в Orr (4) и указано в Orr (5, см. Ссылки), что для случая регрессии хребта GCV может быть записан как
где
- «эффективное число параметров», которое задается
где NumTerms - количество терминов, включенных в модель.
Для RBF «p» - эффективное число параметров, то есть число слагаемых минус корректировка для учёта эффекта сглаживания лямбда в алгоритме аппроксимации. Если лямбда = 0, эффективное число параметров совпадает с числом членов.
Формула для обновления
задается
, где 
На практике предыдущие формулы явно не используются в Orr (5, см. Ссылки). Вместо этого производится разложение сингулярного значения X, и формулы переписываются в терминах собственных значений и собственных векторов матрицы XX '. Это позволяет избежать использования обратной матрицы А, и ее можно использовать для дешевого вычисления GCV для многих значений
. Определение А. см. в разделе Статистика.
В случае Rols компоненты для формулы
вычисляют по формулам, приведенным в Orr [6; см. Ссылки]. Напомним, что матрица регрессии факторизируется во время алгоритма Rols в произведение X = WB. Пусть wj обозначает j-й столбец W, тогда у нас есть
и «эффективное количество параметров» задается
Это эквивалентно «p» (эффективному количеству параметров), определенному в GCV для регрессии хребта.
Формула переоценки для
задается
, где дополнительно
и
Обратите внимание, что эти формулы для Rls не требуют явной инверсии A. Определение A см. в разделе Статистика.
Chen, S., Chng, E.S., Alkadhimi, Регуляризованный ортогональный алгоритм наименьших квадратов для построения радиальных базовых функциональных сетей, Int J. Control, 1996, том 64, № 5, стр. 829-837.
Хассун, М., Основы искусственных нейронных сетей, MIT, 1995.
Орр, М., Введение в радиальные базовые функциональные сети.
Orr, M., Оптимизация ширины радиальных базисных функций.
Орр, М., Регуляризация в выборе центров радиальных базисных функций.
Вендланд, Х., Кусочные многочлены, положительные определенные и компактно поддерживаемые радиальные базисные функции минимальной степени, достижения в вычислительной математике 4 (1995), стр. 389-396.
Гибридные RBF объединяют модель радиальной базовой функции с более стандартными линейными моделями, такими как полиномы или гибридные сплайны. Две детали добавляются вместе для формирования общей модели. Этот подход предлагает возможность сочетать априорные знания, такие как ожидание квадратичного поведения в одной из переменных, с непараметрической природой RBF.
Графический интерфейс пользователя настройки модели для гибридных RBF имеет верхнюю кнопку Set Up, где можно задать алгоритм и опции фитинга. Интерфейс также имеет две вкладки: одна для задания части радиальной базовой функции и одна для детали линейной модели.
Это тот же самый алгоритм, что используется в обычных RBF, то есть управляемый поиск наилучшего параметра ширины.
Этот алгоритм является обобщением StepItRols для RBF. Алгоритм выбирает радиальные базисные функции и члены линейной модели чересстрочным образом, а не в два шага. На каждом шаге выполняется процедура прямого поиска, чтобы выбрать радиальную базисную функцию (с центром, выбранным из набора точек данных) или член линейной модели (выбранный из тех, которые указаны на панели настройки линейной модели), который уменьшает регуляризованную ошибку больше всего. Этот процесс продолжается до тех пор, пока не будет выбрано максимальное количество терминов. Первые несколько терминов добавляются с использованием сохраненного значения лямбда до тех пор, пока не будет достигнуто число терминов, добавляемых до обновления. Затем лямбда итерируется после добавления каждого центра для улучшения GCV.
Параметры подгонки для этого алгоритма следующие:
Максимальное количество терминов: максимальное количество терминов, которые будут выбраны. Значение по умолчанию - количество точек данных.
Максимальное количество центров: максимальное количество членов, которые могут быть радиальными базисными функциями. Значение по умолчанию - четверть точек данных, или 25, в зависимости от того, что меньше.
Примечание
Максимальное количество используемых членов - это комбинация максимального количества центров и числа членов линейной модели. Он ограничен следующим образом:
Максимальное количество использованных членов = Минимум (Максимальное количество членов, Максимальное количество центров + количество членов линейной модели)
В результате модель может иметь больше центров, чем указано в поле Максимальное количество центров, но всегда будет меньше членов, чем (Максимальное количество центров + число членов линейной модели). Количество возможных членов линейной модели можно просмотреть на вкладке Линейная деталь (Linear Part) диалогового окна Настройка глобальной модели (Global Model Setup) (Общее количество элементов).
Процент данных, которые должны быть центрами-кандидатами: процент точек данных, доступных для выбора в качестве центров. Значение по умолчанию - 100% при ≤200 количества точек данных.
Количество терминов, добавляемых перед обновлением: Сколько терминов следует добавить перед началом обновления лямбды.
Минимальное изменение в log10 (GCV): допуск.
Максимальный номер Число шагов в строке, что изменение в log10 (GCV) может быть меньше, чем допуск до завершения алгоритма.
Этот алгоритм начинается с подгонки линейной модели, указанной на панели линейной модели, а затем подгоняет сеть радиальных базисных функций к остаточной. Можно задать члены линейной модели для включения обычным способом с помощью селектора терминов. При необходимости можно активировать пошаговые опции. В этом случае после установки части линейной модели некоторые термины автоматически добавляются или удаляются перед установкой части RBF. Можно выбрать алгоритм и опции, которые используются для соответствия нелинейным параметрам RBF, нажав кнопку Set Up в параметрах обучения RBF.
Определите, какие параметры оказывают наибольшее влияние на посадку, выполнив следующие действия.
Установите значение RBF по умолчанию. Удалите все очевидные отклонения.
Получите приблизительное представление о том, сколько RBF потребуется. Если центр совпадает с точкой данных, он помечается пурпурной звездочкой на графике «Прогнозируемый/наблюдаемый». Расположение центров можно просмотреть в графическом и табличном формате с помощью кнопки панели инструментов Показать центры (View Centers). 
Если вы удаляете отклонение, совпадающее с центром (помеченным звездочкой), выполните переопределение, щелкнув Обновить вписку (Update Fit) на панели инструментов.
Попробуйте использовать несколько ядер. Можно изменить параметры в подгонке, нажав кнопку Настроить (Set Up) в диалоговом окне Выбор модели (Model Selection).
Определите алгоритм выбора основной ширины. Попробуйте с обоими TrialWidths и WidPerDim алгоритмы.
Определите, какие типы ядра выглядят наиболее обнадеживающими.
Сузите соответствующий диапазон ширины для поиска.
Определите алгоритм выбора центра.
Определите алгоритм лямбда-выбора.
Попробуйте изменить параметры в алгоритмах.
Если какие-либо точки кажутся возможными отклонениями, попробуйте подогнать модель как с этими точками, так и без них.
Если на каком-либо этапе вы принимаете решение об изменении, которое оказывает большое влияние (например, удаление отклонения), то необходимо повторить предыдущие шаги, чтобы определить, повлияет ли это на выбранный путь.
Дополнительные сведения о всех параметрах посадки см. в разделе Процедуры фитинга.
Браузер модели имеет быструю опцию для сравнения всех различных ядер RBF и проверки множества центров.
После подгонки RBF по умолчанию выберите глобальную модель RBF в дереве модели.
Щелкните значок панели инструментов Построить модели (Build Models).
Выберите значок RBF в появившемся диалоговом окне Построить модели (Build Models) и нажмите кнопку ОК.
Откроется диалоговое окно «Параметры построения модели». Можно указать диапазон значений для максимального количества центров и щелкнуть Параметры модели (Model settings), чтобы изменить любые другие параметры модели. Используемые значения по умолчанию совпадают с типом родительской модели RBF.
Можно установить флажок Построить все ядра для создания моделей с заданным диапазоном центров для каждого типа ядра в качестве выбора дочерних узлов текущей модели RBF.
Обратите внимание, что это может занять много времени для локальных моделей, поскольку вы создадите альтернативные модели с диапазоном центров для каждого типа ядра для каждой функции ответа; после запуска построения модели всегда можно нажать кнопку «Остановить», чтобы прервать процесс, если он занимает слишком много времени.
Щелкните Создать (Build), чтобы создать указанные модели.
Основным параметром, который необходимо настроить, чтобы получить хорошее соответствие с RBF, является максимальное количество центров. Это параметр алгоритма выбора центра и максимальное количество выбранных центров/RBF.
Как правило, максимальное количество центров - это количество фактически выбранных RBF. Однако иногда выбирается меньшее количество RBF, поскольку (регуляризованная) ошибка упала ниже допуска до достижения максимума.
Следует использовать ряд RBF, значительно меньших, чем количество точек данных, в противном случае в ошибке недостаточно степеней свободы для оценки прогнозирующего качества модели. То есть, вы не можете определить, полезна ли модель, если вы используете слишком много RBF. Мы рекомендуем верхнюю границу 60% по отношению количества RBF к количеству точек данных. Наличие 80 центров, когда есть только 100 точек данных, может, кажется, дать хорошее значение PRESS, но когда дело доходит до проверки, иногда может стать ясно, что данные были переоборудованы, и прогнозирующая способность не так хороша, как предполагает PRESS.
Одной из стратегий выбора количества RBF является размещение большего количества центров, чем вы считаете необходимым (скажем, 70 из 100), а затем использование кнопки панели инструментов Prune для уменьшения количества центров в модели. После обрезки сети запишите уменьшенное количество RBF. Попробуйте снова подогнать модель с максимальным количеством центров, установленным на это уменьшенное число. При этом значения нелинейных параметров (ширина и лямбда) пересчитываются, чтобы быть оптимальными для уменьшенного числа RBF.
Одна из стратегий использования Stepwise состоит в том, чтобы использовать его для минимизации PRESS в качестве окончательной точной настройки для сети, как только будет выполнено обрезание. В то время как Prune позволяет удалить только последний введенный RBF, Stepwise позволяет удалить любой RBF.
Не акцентируйте внимание исключительно на НАЖАТЬ как меру благости подгонки, особенно при больших соотношениях RBF к точкам данных. Также учтите log10 (GCV).
Попробуйте оба TrialWidths и WidPerDim. Второй алгоритм обеспечивает большую гибкость, но является более дорогостоящим в вычислительном отношении. Просмотрите значения ширины в каждом направлении, чтобы увидеть, есть ли существенная разница, чтобы увидеть, стоит ли фокусировать усилия на эллиптических базисных функциях (используйте кнопку панели инструментов «Просмотр модели
»).
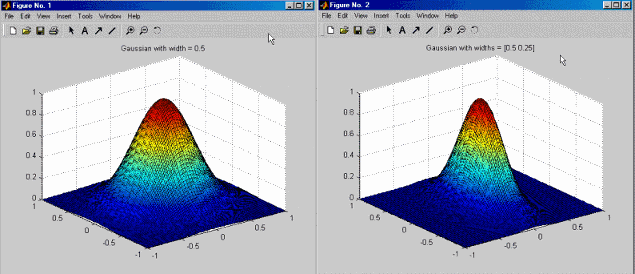
Если используются различные базовые функции, то ширина размеров существенно не изменяется, а значения PRESS/GCV существенно не улучшаются с помощью WidPerDim TrialWidths, затем сосредоточиться на TrialWidthsи просто вернуться к WidPerDim для тонкой настройки на финальных стадиях.
Включить параметр «Отображение» в TrialWidths для просмотра хода выполнения алгоритма. Следите за альтернативными областями в диапазоне ширины, которыми преждевременно пренебрегали. Выходной log10 (GCV) в конечном масштабе должен быть одинаковым для каждой из испытываемых значений ширины; то есть выход должен быть приблизительно плоским. Если это не так, попробуйте увеличить количество зумов.
В TrialWidths, для каждого типа RBF, попробуйте сузить начальный диапазон ширины для поиска. Это может привести к уменьшению числа увеличений.
Трудно дать правила выбора лучшего РФБ, так как лучший выбор сильно зависит от данных. Лучше всего попробовать все их с помощью обоих алгоритмов верхнего уровня (TrialWidths и WidPerDim) и с разумным количеством центров сравните значения PRESS/GCV, затем сосредоточьтесь на тех, которые выглядят наиболее обнадеживающими.
Если мультиквадрики и тонколистовые сплайны дают плохие результаты, стоит попробовать их в сочетании с полиномами низкого порядка в качестве гибридного сплайна. Попробуйте дополнить мультиквадрики постоянным членом и тонколистовыми сплайнами линейными (порядок 1) членами. См. раздел Гибридные радиальные базовые функции.
Следите за проблемами кондиционирования с гауссовыми ядрами (скажем, номер условия > 10 ^ 8).
Следите за странными результатами с функциями Вендланда, когда отношение числа параметров к числу наблюдений высокое. Когда эти функции имеют очень малую ширину, каждая базисная функция вносит вклад в аппроксимацию только в одной точке данных. Это потому, что его поддержка охватывает только одну базисную функцию, которая является его центром. Остатки будут равны нулю в каждой из точек данных, выбранных в качестве центра, и большими в других точках данных. Этот сценарий может указывать на хорошие значения RMSE, но прогнозирующее качество сети будет плохим.
Лямбда - параметр регуляризации.
IterateRols обновляет центры после каждого обновления лямбды. Это делает его более вычислительно интенсивным, но потенциально приводит к лучшей комбинации лямбда и центров.
StepItRols чувствителен к параметру Количество центров для добавления перед обновлением. Включите опцию Display для просмотра уменьшения log10 (GCV) по мере наращивания количества центров.
Изучите графики, созданные с помощью лямбда-алгоритма выбора, проигнорировав предупреждение «Будет создано чрезмерное количество графиков». Приведет ли увеличение допуска или числа начальных испытательных значений лямбда к лучшему выбору лямбда?
По большинству проблем, Rols представляется наиболее эффективным.
Если выбрано меньше максимального количества центров и требуется принудительно выбрать максимальное число, уменьшите допуск до эпсилона (eps).
CenterExchange очень дорого, и не стоит использовать это при больших проблемах. В этом случае другие алгоритмы выбора центра, ограничивающие центры подмножеством точек данных, могут не обеспечить достаточной гибкости.
Попробуйте выполнить команду Пошаговое (Stepwise) после обрезки, а затем обновите модель, установив новое максимальное количество центров на количество терминов, оставшихся после операции Пошаговое (Stepwise).
Обновить подгонку модели после удаления отклонений; используйте кнопку панели инструментов.
Перейдите на линейную панель детали и укажите элементы полинома или сплайна, которые должны отображаться в модели.
Слишком много членов без RBF становится очевидным из-за большого значения лямбды, указывающего на то, что основные тренды учитываются линейной частью. В этом случае следует сбросить начальное значение лямбды (скажем, 0,001) перед следующей посадкой.
Для просмотра сведений о текущей модели в любой модели можно использовать кнопку панели инструментов Вид (View) Модель (Model) или Вид (View) > Определение модели (Model Definition) (или сочетание клавиш CTRL + V). Откроется диалоговое окно Просмотр модели (Model Viewer). Здесь для любой модели RBF можно увидеть тип ядра, количество центров, ширину и параметр регуляризации.
Однако для полного определения формулы модели RBF необходимо также указать местоположения центров и высоту каждой базисной функции. Информация о местоположении центра доступна в диалоговом окне «View Centres», а коэффициенты - в окне «Stepwise». Обратите внимание, что все эти значения находятся в кодированных единицах.
