fminsearch Алгоритмfminsearch использует алгоритм симплекса Нелдера-Мид, как описано в Lagarias et al. [57]. Этот алгоритм использует симплекс из n + 1 точек для n-мерных векторов x. Алгоритм сначала делает симплекс вокруг начального предположения x0, добавляя 5% каждого компонента x0 (i) к x0, и используя эти n векторов в качестве элементов симплекса в дополнение к x0. (Алгоритм использует 0,00025 в качестве компонента i, если x0 ( i) = 0.) Затем алгоритм многократно модифицирует симплекс в соответствии со следующей процедурой.
Примечание
Ключевые слова для fminsearch после описания шага отображается полужирным шрифтом.
Пусть x (i) обозначает список точек в текущем симплексе, i = 1,..., n + 1.
Упорядочивайте точки в симплексе от самого низкого значения функции f (x (1)) до самого высокого f (x (n + 1)). На каждом шаге итерации алгоритм отбрасывает текущую наихудшую точку x (n + 1) и принимает другую точку в симплекс. [Или, в случае шага 7 ниже, он изменяет все n точек со значениями выше f (x (1))].
Создание отраженной точки
r = 2m - x (n + 1),
где
m = Startx (i )/n, i = 1... n,
и вычисляют f (r).
Если f (x (1)) ≤ f (r) < f (x (n)), примите r и завершите эту итерацию. Размышлять
Если f (r) < f (x (1)), вычислите точку расширения s
s = m + 2 (m - x (n + 1)),
и вычислить f (s).
Если f (s) < f (r), примите s и завершите итерацию. Расшириться
В противном случае примите r и завершите итерацию. Размышлять
Если f (r) ≥ f (x (n)), выполните сжатие между m и eitherx (n + 1) или r, в зависимости от которого имеет более низкое значение целевой функции.
Если f (r) < f (x (n + 1)) (то есть r лучше x (n + 1)), вычислите
c = m + (r - m )/2
и вычислить f (c). Если f ( c) < f (r), примите c и завершите итерацию. Договор вне
В противном случае перейдите к шагу 7 (Усадка).
Если f (r) ≥ f (x (n + 1)), вычислите
cc = m + (x (n + 1) - m )/2
и вычислить f (cc). Если f ( cc) < f (x (n + 1)), примите cc и завершите итерацию. Договор внутри
В противном случае перейдите к шагу 7 (Усадка).
Вычислите n точек
v (i) = x (1) + (x (i) - x (1) )/2
и вычисляют f (v (i)), i = 2,..., n + 1. Симплекс на следующей итерации - x (1), v (2),..., v (n + 1). Сжаться
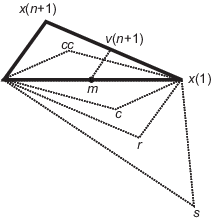
На следующем рисунке показаны точки, которые fminsearch может вычисляться в процедуре вместе с каждым возможным новым симплексом. Исходный симплекс имеет жирный контур. Итерации продолжаются до тех пор, пока они не удовлетворяют критерию остановки.