Неограниченная минимизация - это задача нахождения вектора x, который является локальным минимумом скалярной функции f (x):
)
Термин «неограниченный» означает, что ограничение в диапазоне x не накладывается.
fminunc trust-region АлгоритмМногие методы, используемые в решателях Optimization Toolbox™, основаны на областях доверия, простой, но мощной концепции оптимизации.
Чтобы понять подход доверительной области к оптимизации, рассмотрим задачу неограниченной минимизации, минимизируйте f (x), где функция принимает векторные аргументы и возвращает скаляры. Предположим, что вы находитесь в точке x в n-пространстве и хотите улучшить, т.е. переместитесь в точку с меньшим значением функции. Основная идея состоит в том, чтобы аппроксимировать f более простой функцией q, которая разумно отражает поведение функции f в окрестности N вокруг точки x. Эта окрестность является областью доверия. Пробный этап s вычисляется путем минимизации (или приблизительно минимизации) над N. Это подпроблема области доверия,
| }. | (1) |
Текущая точка обновляется до x + s, если f ( x + s ) < f (x); в противном случае текущая точка остается неизменной, и N, область доверия, уменьшается, и вычисление пробного этапа повторяется.
Ключевые вопросы при определении конкретного подхода области доверия к минимизации f (x) заключаются в том, как выбрать и вычислить аппроксимацию q (определенную в текущей точке x), как выбрать и изменить область доверия N и как точно решить подпроблему области доверия. В этом разделе рассматривается неограниченная проблема. В последующих разделах обсуждаются дополнительные осложнения из-за наличия ограничений на переменные.
В стандартном способе доверительной области ([48]) квадратичное приближение q определяется первыми двумя членами приближения Тейлора к F при x; окрестность N обычно имеет сферическую или эллипсоидальную форму. Математически обычно указывается подпроблема области доверия
| }, | (2) |
где g - градиент f в текущей точке x, H - гессеновская матрица (симметричная матрица вторых производных), D - диагональная масштабная матрица, Δ - положительный скаляр, а ∥. ∥ - 2-норма. Существуют хорошие алгоритмы для решения уравнения 2 (см. [48]); такие алгоритмы обычно включают вычисление всех собственных значений H и процесс Ньютона, применяемый к светскому уравнению
Такие алгоритмы обеспечивают точное решение уравнения 2. Однако они требуют времени, пропорционального нескольким факторизациям Х. Поэтому для масштабных проблем необходим другой подход. Несколько аппроксимационных и эвристических стратегий, основанных на уравнении 2, были предложены в литературе ([42] и [50]). Подход аппроксимации, используемый в решателях Optimization Toolbox, заключается в ограничении подпроблемы области доверия двумерным подпространством S ([39] и [42]). После вычисления подпространства S работа по решению уравнения 2 является тривиальной, даже если необходима полная информация о собственном значении/собственном векторе (поскольку в подпространстве задача является только двумерной). Доминирующая работа теперь перешла к определению подпространства.
Двумерное подпространство S определяют с помощью процесса предварительно кондиционированного сопряженного градиента, описанного ниже. Решатель определяет S как линейное пространство, охватываемое s1 и s2, где s1 находится в направлении градиента g, а s2 является либо приближенным направлением Ньютона, т.е. решением
| (3) |
или направление отрицательной кривизны,
| (4) |
Философия, лежащая в основе этого выбора S, состоит в том, чтобы форсировать глобальную сходимость (через самое крутое направление спуска или отрицательное направление кривизны) и достичь быстрой локальной сходимости (через шаг Ньютона, когда она существует).
Эскиз неограниченной минимизации с использованием идей области доверия теперь легко дать:
Сформулируйте двухмерную подпроблему области доверия.
Решите уравнение 2, чтобы определить пробный этап s.
Если f (x + s) < f (x), то x = x + s.
Отрегулируйте Δ.
Эти четыре шага повторяются до сходимости. Измерение Δ области доверия корректируется в соответствии со стандартными правилами. В частности, он уменьшается, если стадия испытания не принимается, то есть f (x + s) ≥ f (x). Для обсуждения этого аспекта см. [46] и [49].
Решатели Optimization Toolbox рассматривают несколько важных особых случаев f со специализированными функциями: нелинейные наименьшие квадраты, квадратичные функции и линейные наименьшие квадраты. Однако лежащие в основе алгоритмические идеи те же, что и для общего случая. Эти особые случаи рассматриваются в последующих разделах.
Популярным способом решения больших, симметричных, положительных определённых систем линейных уравнений Hp = -g является метод Предварительно кондиционированных сопряжённых градиентов (PCG). Этот итеративный подход требует возможности вычисления матрично-векторных произведений формы H· v, где v - произвольный вектор. Симметричная положительная определенная матрица М является предварительным условием для Н. То есть М = C2, где C-1HC-1 является хорошо кондиционированной матрицей или матрицей с кластеризованными собственными значениями .
В контексте минимизации можно предположить, что матрица Гессена H симметрична. Однако H гарантированно является положительным определенным только в районе сильного минимизатора. Алгоритм PCG выходит, когда он сталкивается с направлением отрицательной (или нулевой) кривизны, то есть dTHd ≤ 0. Направление р выхода PCG является либо направлением отрицательной кривизны, либо приближенным решением для системы Ньютона Hp = -g. В любом случае p помогает определить двумерное подпространство, используемое в подходе «доверительная область», обсуждаемом в документе «Методы доверительной области для нелинейной минимизации».
fminunc quasi-newton АлгоритмХотя существует широкий спектр методов для неограниченной оптимизации, методы могут быть широко классифицированы в терминах производной информации, которая используется или не используется. Методы поиска, использующие только оценки функций (например, симплексный поиск Nelder и Mead [30]), наиболее подходят для проблем, которые не являются гладкими или имеют ряд разрывов. Градиентные методы обычно более эффективны, когда функция, подлежащая минимизации, является непрерывной в своей первой производной. Методы более высокого порядка, такие как метод Ньютона, действительно подходят только тогда, когда информация второго порядка легко и легко вычисляется, потому что вычисление информации второго порядка, используя численное дифференцирование, является вычислительно дорогостоящим.
Градиентные методы используют информацию о наклоне функции, чтобы диктовать направление поиска, где минимум считается лежащим. Простейшим из них является метод наиболее крутого спуска, при котором поиск выполняется в направлении, - ∇f (x), где ∇f (x) - градиент целевой функции. Этот метод очень неэффективен, когда функция, подлежащая минимизации, имеет длинные узкие впадины, как, например, в случае функции Розенброка
| (1 − x1) 2. | (5) |
Минимум этой функции имеет значение x = [1,1], где f (x ) = 0. Контурная карта этой функции показана на рисунке ниже вместе с траекторией решения до минимума для наиболее крутой реализации спуска, начинающейся в точке [-1.9.2]. Оптимизация была завершена после 1000 итераций, всё ещё на значительном расстоянии от минимума. Черные области находятся там, где метод постоянно зигзагирует с одной стороны долины на другую. Заметим, что к центру участка делается ряд более крупных шагов, когда точка приземляется точно в центре долины.
Рисунок 5-1, Метод самого крутого спуска по функции Розенброка
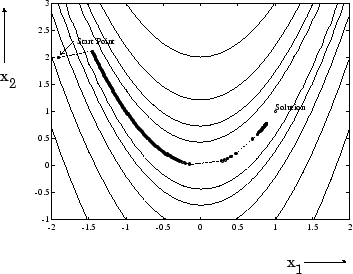
Эта функция, также известная как функция банана, известна в неограниченных примерах из-за того, как кривизна изгибается вокруг начала координат. Функция Розенброка используется во всем этом разделе для иллюстрации использования различных методов оптимизации. Контуры были нанесены экспоненциальными приращениями из-за крутизны склона, окружающего U-образную долину.
Более полное описание этого рисунка, включая сценарии, генерирующие итеративные точки, см. в разделе Минимизация функции банана.
Из методов, использующих информацию о градиенте, наиболее предпочтительными являются методы квази-Ньютона. Эти методы создают информацию о кривизне на каждой итерации, чтобы сформулировать задачу квадратной модели формы
| + b, | (6) |
где матрица Гессена, H, является положительной определенной симметричной матрицей, c - постоянным вектором, а b - константой. Оптимальное решение для этой задачи возникает, когда частные производные x переходят к нулю, то есть
| + c = 0. | (7) |
Оптимальная точка решения, x *, может быть записана как
| − 1c. | (8) |
Методы типа Ньютона (в отличие от методов квази-Ньютона) вычисляют H непосредственно и идут в направлении спуска, чтобы найти минимум после ряда итераций. Вычисление Н численно включает в себя большое количество вычислений. Квази-ньютоновские методы избегают этого, используя наблюдаемое поведение f (x) и ∇f (x) для формирования информации о кривизне, чтобы сделать приближение к H с помощью соответствующей методики обновления.
Разработано большое количество гессенских методов обновления. Однако формула Бройдена [3], Флетчера [12], Гольдфарба [20] и Шанно [37] (BFGS) считается наиболее эффективной для использования в способе общего назначения.
Формула, заданная BFGS,
| HkskTHkTskTHksk, | (9) |
где
(xk).
В качестве начальной точки H0 можно задать любую симметричную положительную определенную матрицу, например единичную матрицу I. Чтобы избежать инверсии гессенского H, можно вывести метод обновления, который позволяет избежать прямой инверсии H, используя формулу, которая делает аппроксимацию обратного гессенского H-1 при каждом обновлении. Хорошо известной процедурой является формула DFP Давидона [7], Флетчера и Пауэлла [14]. Используется та же формула, что и метод BFGS (уравнение 9), за исключением того, что qk заменен на sk.
Информацию о градиенте либо подают через аналитически рассчитанные градиенты, либо получают с помощью частных производных с использованием метода численного дифференцирования посредством конечных разностей. Это включает в себя возмущение каждой из конструктивных переменных, x, в свою очередь, и вычисление скорости изменения целевой функции.
При каждой большой итерации k выполняется поиск строки в направлении
| ). | (10) |
Метод квази-Ньютона иллюстрируется путем решения функции Розенброка на рис. 5-2, Метод BFGS по функции Розенброка. Метод способен следовать форме долины и сходится к минимуму после оценки 140 функций, используя только градиенты конечных разностей.
Рисунок 5-2, Метод BFGS по функции Розенброка
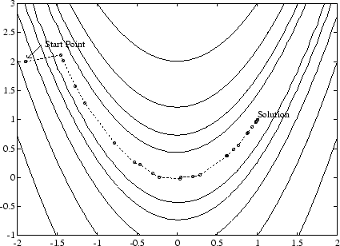
Более полное описание этого рисунка, включая сценарии, генерирующие итеративные точки, см. в разделе Минимизация функции банана.
Поиск по строкам - это метод поиска, который используется как часть алгоритма оптимизации большего размера. На каждом шаге основного алгоритма методом «линия-поиск» осуществляется поиск по линии, содержащей текущую точку xk, параллельную направлению поиска, которая является вектором, определяемым основным алгоритмом. То есть метод находит следующий итерат xk + 1 формы
| α * dk, | (11) |
где xk обозначает текущий итерат, dk - направление поиска, а α * - параметр длины скалярного шага.
Метод поиска линии пытается уменьшить целевую функцию вдоль линии xk + α * dk, многократно минимизируя модели полиномиальной интерполяции целевой функции. Процедура поиска строки состоит из двух основных шагов:
Фаза скобки определяет диапазон точек на линии + α * dk для поиска. Скобка соответствует интервалу, определяющему диапазон значений α.
Шаг секционирования делит скобку на субинтервалы, на которых минимум целевой функции аппроксимируется полиномиальной интерполяцией.
Результирующая длина шага α удовлетворяет условиям Вольфа:
| +c1α∇fkTdk, | (12) |
| Tdk≥c2∇fkTdk, | (13) |
где c1 и c2 - константы с 0 < c1 < c2 < 1.
Первое условие (уравнение 12) требует, чтобы αk в достаточной степени уменьшало целевую функцию. Второе условие (уравнение 13) гарантирует, что длина шага не слишком мала. Точки, удовлетворяющие обоим условиям (уравнение 12 и уравнение 13), называются приемлемыми точками.
Способ поиска линии представляет собой реализацию алгоритма, описанного в разделе 2-6 [13]. Для получения дополнительной информации о поиске строк см. также [31].
Многие из функций оптимизации определяют направление поиска, обновляя матрицу Гессена на каждой итерации, используя метод BFGS (уравнение 9). Функция fminunc также предоставляет возможность использовать метод DFP, заданный в Quasi-Newton Methods (set HessUpdate кому 'dfp' в options для выбора метода DFP). Гессен, Н, всегда поддерживается положительным определенным, так что направление поиска d всегда находится в направлении спуска. Это означает, что для некоторого произвольно малого шага α в направлении d целевая функция уменьшается по величине. Вы достигаете положительной определенности H, гарантируя, что H инициализирован как положительный определенный, и после этого (из уравнения 14) всегда положителен. Термин является произведением параметра αk длины шага поиска линии и комбинации направления d поиска с оценками прошлых и нынешних градиентов.
| (xk) Td). | (14) |
Вы всегда достигаете условия, что является положительным, выполняя достаточно точный поиск линии. Это происходит потому, что направление поиска, d, является направлением спуска, так что αk и отрицательный градиент - ∇f (xk) Td всегда положительны. Таким образом, возможный отрицательный член - ∇f (xk + 1) Td может быть сделан настолько малым по величине, насколько это требуется, путем повышения точности поиска линии.