Exponenta Banner
exponenta event banner

Одномерные полупредельные зависимости

Найти значения x, которые минимизируют

f (x) = (x1-0,5) 2 + (x2- 0,5) 2 + (x3- 0,5) 2

где

K1 (x, w1) = sin (w1x1) cos (w1x2) − 11000 (w1 − 50) 2 − sin (w1x3) −x3≤1,K2 (x, w2) = sin (w2x2) cos (w2x1) − 11000 (w2 − 50) 2 − sin (w2x3) −x3≤1,

для всех значений w1 и w2 в диапазонах

1 ≤ w1 ≤ 100,
1 ≤ w2 ≤ 100.

Обратите внимание, что полулегкие зависимости являются одномерными, то есть векторами. Поскольку ограничения должны иметь вид Ki (x,  wi) ≤ 0, необходимо вычислить ограничения как

K1 (x, w1) = sin (w1x1) cos (w1x2) − 11000 (w1 − 50) 2 − sin (w1x3) −x3−1≤0,K2 (x, w2) = sin (w2x2) cos (w2x1) − 11000 (w2 − 50) 2 − sin (w2x3) −x3−1≤0.

Сначала напишите файл, в котором вычисляется целевая функция.

function f = myfun(x,s)
% Objective function
f = sum((x-0.5).^2);

Во-вторых, напишите файл mycon.m вычисляет нелинейные ограничения равенства и неравенства и полубесконечные ограничения.

function [c,ceq,K1,K2,s] = mycon(X,s)
% Initial sampling interval
if isnan(s(1,1)),
   s = [0.2 0; 0.2 0];
end
% Sample set
w1 = 1:s(1,1):100;
w2 = 1:s(2,1):100;

% Semi-infinite constraints 
K1 = sin(w1*X(1)).*cos(w1*X(2)) - 1/1000*(w1-50).^2 -...
       sin(w1*X(3))-X(3)-1;
K2 = sin(w2*X(2)).*cos(w2*X(1)) - 1/1000*(w2-50).^2 -...
       sin(w2*X(3))-X(3)-1;

% No finite nonlinear constraints
c = []; ceq=[];

% Plot a graph of semi-infinite constraints
plot(w1,K1,'-',w2,K2,':')
title('Semi-infinite constraints')
drawnow

Затем вызовите подпрограмму оптимизации.

x0 = [0.5; 0.2; 0.3];      % Starting guess
[x,fval] = fseminf(@myfun,x0,2,@mycon);

После восьми итераций решение будет

x
x =
    0.6675
    0.3012
    0.4022

Значение функции и максимальные значения полулегких ограничений в решении x являются

fval
fval =
    0.0771

[c,ceq,K1,K2] = mycon(x,NaN); % Initial sampling interval
max(K1)
ans =
   -0.0077
max(K2)
ans =
   -0.0812

Создается график полулегких ограничений.

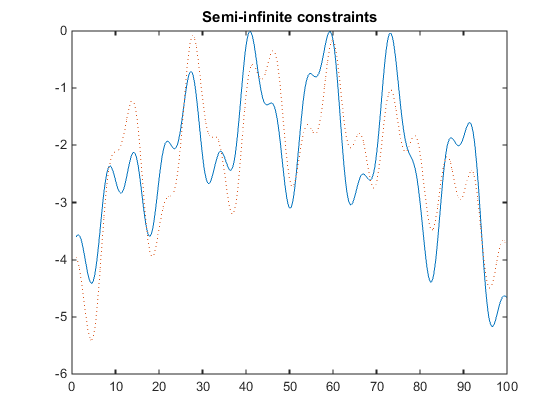
На этом графике показано, как пики в обеих зависимостях находятся на границе зависимости.

Команда печати внутри mycon.m замедляет вычисления. Удалите эту линию, чтобы увеличить скорость.

См. также

Связанные темы

Документация по панели инструментов оптимизации

Поддержка