fmincon Решающее устройствоВ этом примере показано, как использовать задачу «Оптимизировать Live Editor» с fmincon решатель для минимизации квадратичной зависимости от линейных и нелинейных ограничений и границ.
Рассмотрим проблему поиска [x1, x2], которая решает
+ x22
с учетом ограничений
Начальная точка x0 для этой задачи x1 = 3 и x2 = 1.
Создайте новый сценарий в реальном времени, нажав кнопку «Создать сценарий в реальном времени» в разделе «Файл» на вкладке «Главная».
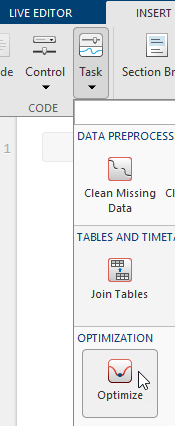
Вставка задачи «Оптимизировать интерактивный редактор». Перейдите на вкладку Вставка, а затем в разделе Код выберите Задача > Оптимизировать.
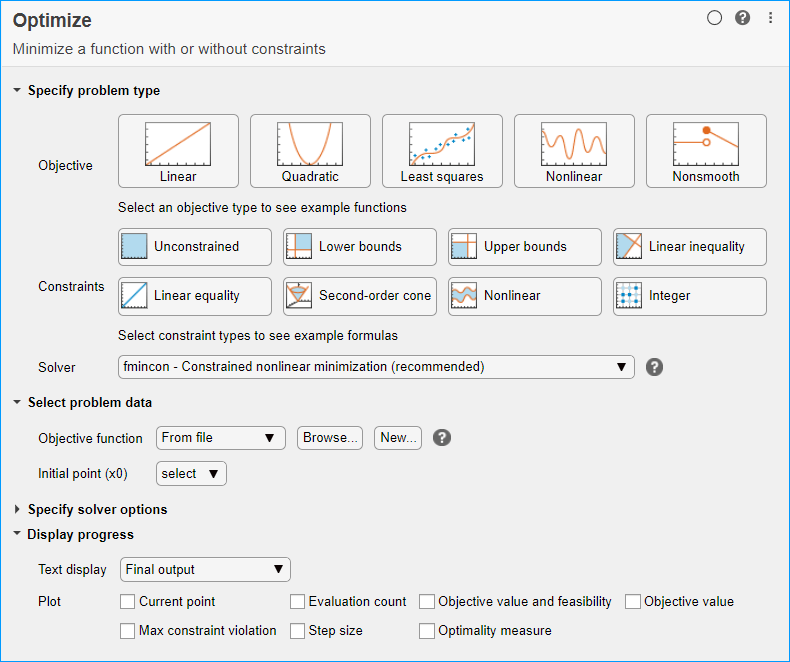
Для последующего использования при вводе данных о проблемах выберите «Вставка» > «Разрыв сечения». Новые разделы появляются над и под задачей.
Начиная с верхней части задачи введите тип проблемы и типы ограничений. Нажмите кнопку «Цель» > «Квадратичный» и кнопки «Ограничения» > «Нижние границы», «Линейное неравенство» и «Нелинейное». Задача показывает, что рекомендуемый решатель fmincon.
Целевая функция
Целевая функция достаточно проста для представления в виде анонимной функции. Установите курсор в разделе над задачей и введите этот код.
fun = @(x)sum(x.^2);
Нижняя граница
Проблема содержит нижнюю границу x1 ≥ 0,5. Выразить эту привязку как переменную lb. Установив курсор в конце строки, определяющей целевую функцию, нажмите Enter и введите следующий код для задания нижней границы.
lb = [0.5 -Inf];
Начальная точка
Установив курсор в конце линии, определяющей нижнюю границу, нажмите Enter и введите следующий код для установки начальной точки.
x0 = [3,1];
Линейная зависимость
Установив курсор в конце линии, определяющей начальную точку, нажмите Enter и введите следующий код для задания линейной зависимости.
A = [-1,-1]; b = -1;
Выполнить раздел
Верхняя часть теперь включает пять параметров.
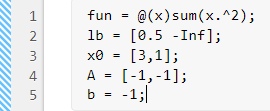
Затем необходимо запустить раздел для размещения параметров в рабочей области в качестве переменных. Для этого щелкните крайнюю левую область сечения, содержащую полосу диагональных полос. После щелчка на этой области панель становится сплошной, указывая, что переменные теперь находятся в рабочем пространстве. (Примечание: Можно также нажать Ctrl + Enter, чтобы запустить раздел .)
Задать данные проблемы
Введите переменные в разделе «Выбор данных проблемы» задачи. Чтобы указать целевую функцию, выберите Целевая функция > Дескриптор функции и выберите веселье.
Задайте начальную точку x0.
Выберите Нижние границы (Lower bounds) > Из рабочей области (From workspace) и выберите lb.
Установка переменных ограничения линейного неравенства A и b в области Линейное неравенство.
Теперь задайте нелинейные ограничения неравенства. В разделе Выбор данных проблемы выберите Нелинейная > Локальная функция, а затем нажмите кнопку Создать. Функция появится в новом разделе под задачей. Отредактируйте результирующий код, чтобы он содержал следующие незафиксированные строки.
function [c,ceq] = constraintFcn(x) % You can include commented code lines or not. % Be sure that just these uncommented lines remain: c = [-x(1)^2 - x(2)^2 + 1; -9*x(1)^2 - x(2)^2 + 9; -x(1)^2 + x(2); -x(2)^2 + x(1)]; ceq = []; end
В разделе Выбор данных проблемы выберите функцию constraintFcn.
Мониторинг хода выполнения
В разделе Ход выполнения задачи выберите Просмотр текста > Каждая итерация, чтобы можно было контролировать ход выполнения решателя. Выберите целевое значение для графика.
Ваша настройка выглядит следующим образом:
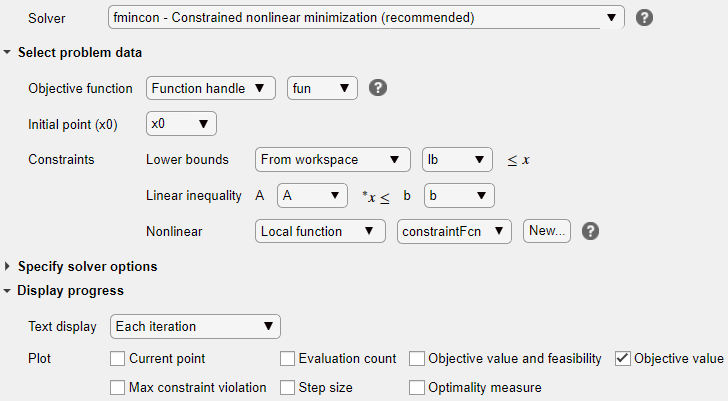
Чтобы запустить решатель, нажмите кнопку опций ⁝ в правом верхнем углу окна задачи и выберите Выполнить раздел.
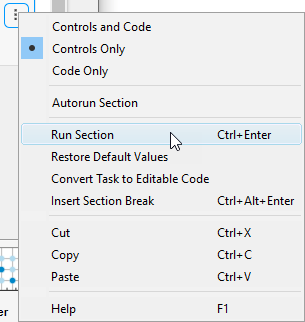
График отображается в отдельном окне рисунка и в области вывода задания.
Чтобы увидеть, где возвращаются переменные решения, посмотрите в верхней части задачи.
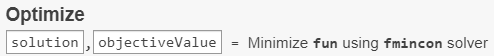
Конечная точка и связанное с ней значение целевой функции отображаются в solution и objectiveValue переменные в рабочей области. Просмотрите эти значения, введя этот код в разделе редактора под задачей.
solution, objectiveValue
Нажмите Ctrl + Enter, чтобы запустить раздел.
![solution = [1 1], objectiveValue = 2](optimizelet_fmincon_answer.png)